Create Binary Tree From Descriptions
MediumYou are given a 2D integer array descriptions where descriptions[i] = [parenti, childi, isLefti] indicates that parenti is the parent of childi in a binary tree of unique values. Furthermore,
- If
isLefti == 1, thenchildiis the left child ofparenti. - If
isLefti == 0, thenchildiis the right child ofparenti.
Construct the binary tree described by descriptions and return its root.
The test cases will be generated such that the binary tree is valid.
Example 1:
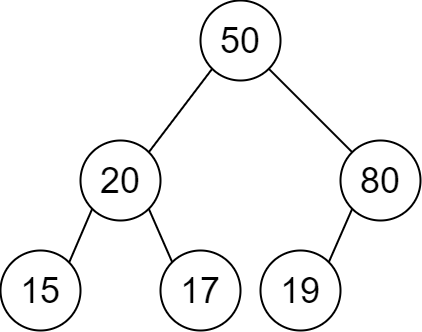
Input: descriptions = [[20,15,1],[20,17,0],[50,20,1],[50,80,0],[80,19,1]] Output: [50,20,80,15,17,19] Explanation: The root node is the node with value 50 since it has no parent. The resulting binary tree is shown in the diagram.
Example 2:
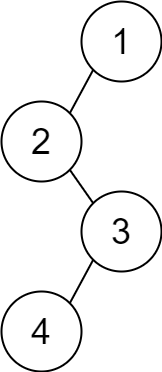
Input: descriptions = [[1,2,1],[2,3,0],[3,4,1]] Output: [1,2,null,null,3,4] Explanation: The root node is the node with value 1 since it has no parent. The resulting binary tree is shown in the diagram.
Constraints:
1 <= descriptions.length <= 104descriptions[i].length == 31 <= parenti, childi <= 1050 <= isLefti <= 1- The binary tree described by
descriptionsis valid.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the node values in the descriptions? Can they be negative or zero?
- Is it guaranteed that the input describes a valid tree structure, or should I handle cases where it does not (e.g., cycles, multiple roots)?
- If a node is described as both a child and a parent, which description takes precedence?
- What should I return if the input descriptions are empty or do not describe any tree at all? Should I return null or an empty tree?
- Are there any memory constraints I should be aware of when constructing the tree, given potentially large input descriptions?
Brute Force Solution
Approach
We're given a list of parent-child relationships that describe a binary tree. The brute force method involves checking every single description and slowly building the tree by trying out every possible connection between the parent and child nodes until we get it right.
Here's how the algorithm would work step-by-step:
- First, look at all the descriptions and identify all the unique numbers representing nodes.
- Assume that any node can be the root, so we initially consider each node as a potential root.
- For each potential root, go through the descriptions and try to connect the children to the parent nodes, creating a tree structure.
- Check if a given description already fits to the structure created, move on to the next one.
- If it doesn't fit, we can either ignore that description and try other combinations, or go back and choose a different structure.
- After trying all possible combinations with different nodes being considered as root, we see which combination follows all the rules from the descriptions.
- If there is only one result, that's the correct binary tree.
Code Implementation
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def create_binary_tree_from_descriptions(descriptions):
all_nodes = set()
for parent_value, child_value, is_left in descriptions:
all_nodes.add(parent_value)
all_nodes.add(child_value)
possible_roots = list(all_nodes)
for potential_root_value in possible_roots:
root = TreeNode(potential_root_value)
node_map = {potential_root_value: root}
is_valid_tree = True
for parent_value, child_value, is_left in descriptions:
if parent_value not in node_map:
node_map[parent_value] = TreeNode(parent_value)
if child_value not in node_map:
node_map[child_value] = TreeNode(child_value)
parent_node = node_map[parent_value]
child_node = node_map[child_value]
# Check if the description is already satisfied.
if is_left:
if parent_node.left is not None and parent_node.left != child_node:
is_valid_tree = False
break
parent_node.left = child_node
else:
if parent_node.right is not None and parent_node.right != child_node:
is_valid_tree = False
break
parent_node.right = child_node
# Check for multiple roots.
parents = set()
for parent_value, child_value, _ in descriptions:
parents.add(parent_value)
children = set()
for _, child_value, _ in descriptions:
children.add(child_value)
root_candidates = parents.difference(children)
if len(root_candidates) != 1 or root.value not in root_candidates:
is_valid_tree = False
if is_valid_tree:
return root
return NoneBig(O) Analysis
Optimal Solution
Approach
We're given descriptions of parent-child relationships and need to construct a tree. Instead of recursively searching or trying to build the tree from the root down, the clever approach is to first identify the root and then build the tree by linking children to their parents using a helper lookup structure.
Here's how the algorithm would work step-by-step:
- First, go through all the descriptions to figure out which node is the root of the tree. A node is the root if it's a parent but never a child.
- Next, create a way to quickly look up each node based on its value. This lookup structure (like a dictionary) will allow us to easily find the correct nodes as we construct the tree.
- Now, go through the descriptions again. For each description, find the parent and child nodes using the lookup structure.
- Link the child node to its parent in the tree structure.
- Repeat the previous two steps until all descriptions have been processed. At this point, the tree should be fully formed.
- Finally, return the root node to represent the whole tree.
Code Implementation
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def create_binary_tree_from_descriptions(descriptions):
child_values = set()
node_map = {}
for parent_value, child_value, is_left in descriptions:
child_values.add(child_value)
if parent_value not in node_map:
node_map[parent_value] = TreeNode(parent_value)
if child_value not in node_map:
node_map[child_value] = TreeNode(child_value)
root_value = None
for parent_value, _, _ in descriptions:
if parent_value not in child_values:
root_value = parent_value
break
#Ensure root exists
if root_value is None:
return None
# Use description to build the tree
for parent_value, child_value, is_left in descriptions:
parent_node = node_map[parent_value]
child_node = node_map[child_value]
# Link children to parents
if is_left:
parent_node.left = child_node
else:
parent_node.right = child_node
return node_map[root_value]Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty descriptions array | Return null or an empty tree as no tree structure can be created from empty descriptions. |
| Descriptions array with only one element. | Create a single node tree; the root will be the parent of that one description element if it's not present in child values, otherwise return null (invalid input). |
| Descriptions form a cycle, leading to an infinite recursion during tree construction. | Maintain a 'visited' set to detect cycles and return null if a cycle is detected during tree construction. |
| Multiple nodes claim the same parent (invalid tree structure). | If a parent already has a left or right child as specified in a new description, handle the conflict, perhaps by choosing the first child encountered and ignoring subsequent ones, or throwing an error, depending on requirements. |
| Parent node not found in descriptions, resulting in an orphaned subtree. | If a parent is not already present when processing a child, create the parent node immediately; otherwise, track or return null because a root node should appear somewhere. |
| Input describes a forest (multiple disconnected trees) instead of a single tree. | Identify the root nodes (those without parents) and construct the separate trees, then return them as a list of root nodes instead of a single root node if the problem permits forest output. |
| Integer overflow in node values if node values are very large. | Use a data type capable of representing the largest possible node value, or throw an exception if a value exceeds the representable range. |
| Descriptions contain duplicate parent-child relationships. | The solution should handle duplicates gracefully, either by ignoring redundant entries or by ensuring that duplicate entries do not overwrite existing valid tree structures; a set can prevent redundant tree construction. |