Shortest Path in Binary Matrix
MediumGiven an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.
A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:
- All the visited cells of the path are
0. - All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).
The length of a clear path is the number of visited cells of this path.
Example 1:
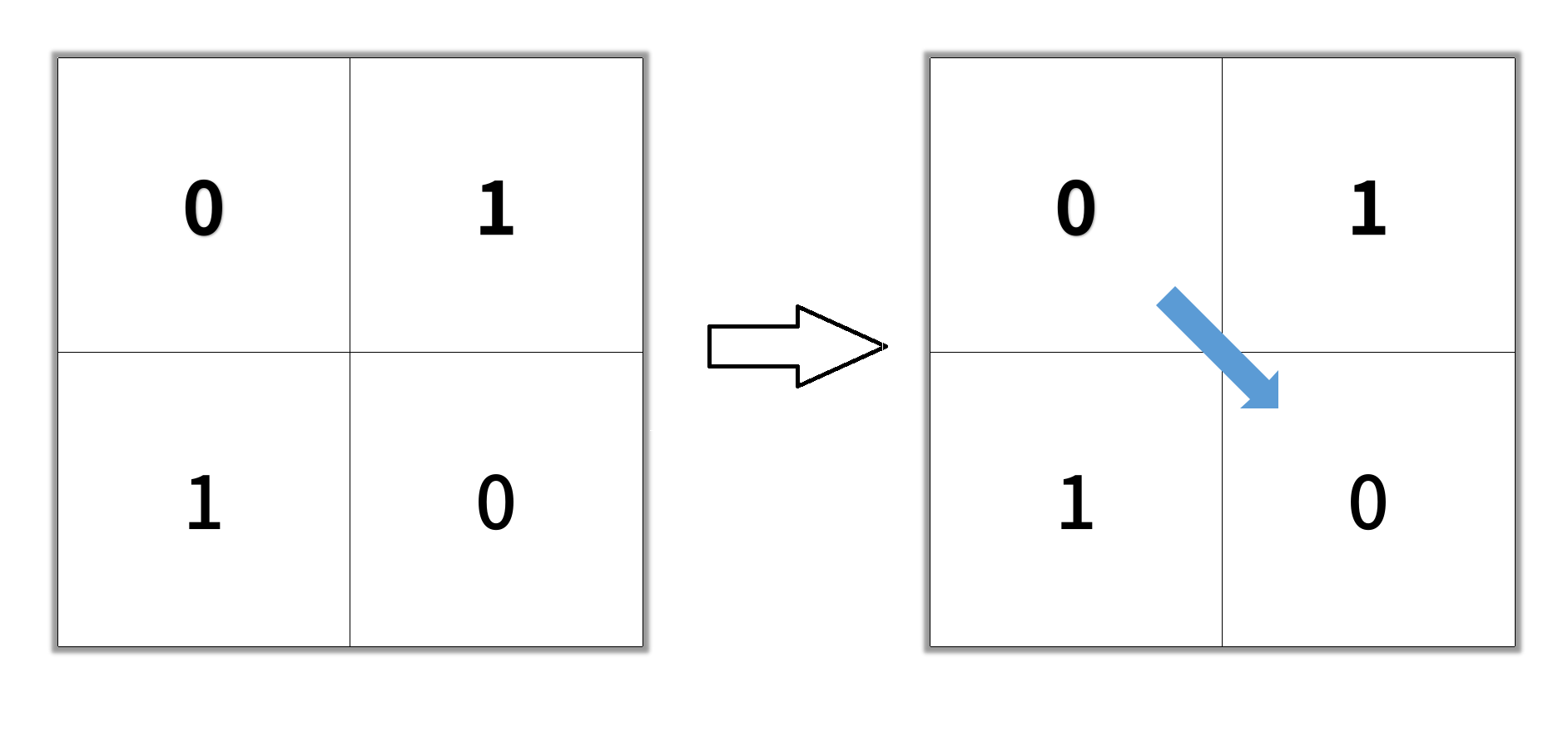
Input: grid = [[0,1],[1,0]] Output: 2
Example 2:
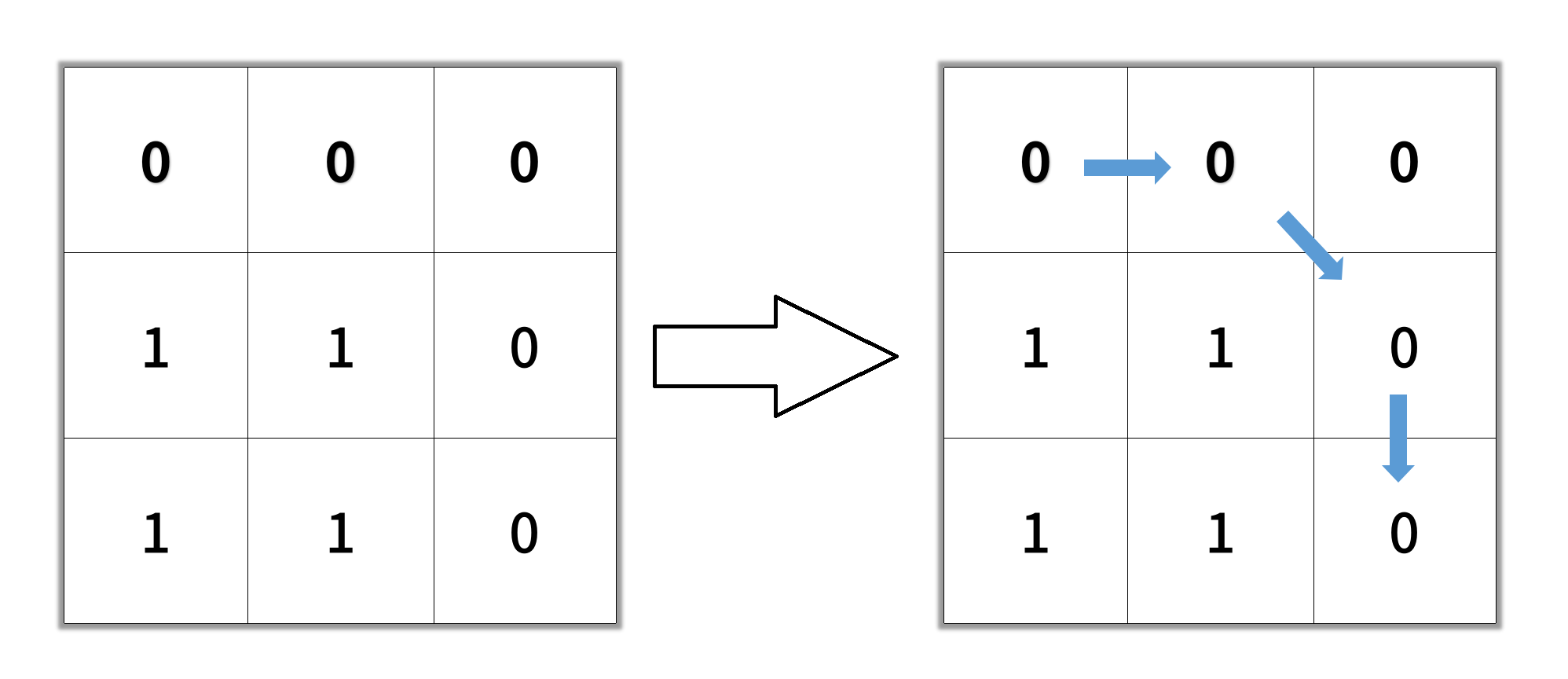
Input: grid = [[0,0,0],[1,1,0],[1,1,0]] Output: 4
Example 3:
Input: grid = [[1,0,0],[1,1,0],[1,1,0]] Output: -1
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 100grid[i][j] is 0 or 1
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the size of the grid (n)? What is the maximum possible value of n?
- Is it guaranteed that the starting cell (0, 0) and the ending cell (n-1, n-1) will always be open (value 0)?
- If there is no path, should I return -1, or is there any other specific value I should return in that case?
- Is the grid guaranteed to be a square matrix (n x n), or could it be a rectangular matrix (m x n)? If it's rectangular, are m and n given separately?
- By 'length of the shortest path', do you mean the number of cells visited (including the start and end), or the number of steps taken (excluding the start)?
Brute Force Solution
Approach
We want to find the shortest path from the top-left corner to the bottom-right corner of a grid, only moving through clear cells. The brute force approach explores every possible path, no matter how long or winding, to find the shortest one. This is like trying every single route you could possibly take, even the ridiculously long ones, before figuring out the best way to get there.
Here's how the algorithm would work step-by-step:
- Start at the top-left corner of the grid.
- From the starting cell, try moving to every possible adjacent clear cell (up, down, left, right, and diagonals).
- For each of those moves, again try moving to every possible adjacent clear cell.
- Continue this process of exploring every possible path, even if it doubles back or goes in circles.
- If a path reaches the bottom-right corner, remember its length (the number of steps it took).
- Keep trying every possible path, even after you've found one that reaches the end, to see if there's an even shorter path.
- Once you've explored all possible paths (or a very, very large number of them), compare the lengths of all the paths that reached the bottom-right corner.
- The shortest of these paths is the answer.
Code Implementation
def shortest_path_binary_matrix_brute_force(grid):
grid_length = len(grid)
if grid[0][0] == 1 or grid[grid_length - 1][grid_length - 1] == 1:
return -1
shortest_path = float('inf')
def is_valid(row, col):
return 0 <= row < grid_length and 0 <= col < grid_length and grid[row][col] == 0
def explore_path(row, col, current_path_length):
nonlocal shortest_path
# If out of bounds or blocked, path is invalid
if not is_valid(row, col):
return
# If we reach the destination, update the shortest path
if row == grid_length - 1 and col == grid_length - 1:
shortest_path = min(shortest_path, current_path_length)
return
# Mark the current cell as visited to avoid cycles
grid[row][col] = 1
# Explore all 8 possible directions
for row_offset in [-1, 0, 1]:
for col_offset in [-1, 0, 1]:
if row_offset == 0 and col_offset == 0:
continue
new_row = row + row_offset
new_col = col + col_offset
explore_path(new_row, new_col, current_path_length + 1)
# Backtrack: reset the cell to 0 for other paths
grid[row][col] = 0
explore_path(0, 0, 1)
if shortest_path == float('inf'):
return -1
else:
return shortest_pathBig(O) Analysis
Optimal Solution
Approach
We want to find the shortest path from the top-left corner to the bottom-right corner of a grid, moving only through cells marked with a zero. We can think of this as a maze where we need to find the most efficient route. We can use a technique that explores the grid layer by layer, outwards from the starting point, until we reach the destination.
Here's how the algorithm would work step-by-step:
- Start at the beginning location.
- Look at all the valid places you can go from your current location. Valid means it's a zero and you haven't been there yet.
- Mark all those reachable places as being one step away from the start.
- Now, from each of those new spots, look at all the valid places you can go that haven't been visited yet.
- Mark those places as being one step further away.
- Continue exploring layer by layer, always moving outward to new, unvisited, valid locations.
- If you eventually reach the destination, the number of steps it took is the shortest path.
- If you explore the entire grid and never reach the destination, then there's no valid path.
Code Implementation
def shortest_path_binary_matrix(grid):
grid_length = len(grid)
if grid[0][0] == 1 or grid[grid_length - 1][grid_length - 1] == 1:
return -1
queue = [(0, 0, 1)]
visited = set()
visited.add((0, 0))
# Possible movements in 8 directions
directions = [(0, 1), (0, -1), (1, 0), (-1, 0),
(1, 1), (1, -1), (-1, 1), (-1, -1)]
while queue:
row, col, path_length = queue.pop(0)
if row == grid_length - 1 and col == grid_length - 1:
return path_length
for row_direction, col_direction in directions:
new_row = row + row_direction
new_col = col + col_direction
# Boundary and validity checks
if 0 <= new_row < grid_length and 0 <= new_col < grid_length and \
grid[new_row][new_col] == 0 and (new_row, new_col) not in visited:
# Mark as visited to avoid cycles
visited.add((new_row, new_col))
queue.append((new_row, new_col, path_length + 1))
# If no path is found
return -1Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty input grid | Return -1 immediately as there's no path to search within an empty grid. |
| Grid with dimensions 0x0 | Return -1 because there is no path in a grid with no dimensions. |
| Grid with dimensions 1x1 where grid[0][0] == 1 | Return -1 as the starting cell is blocked, making a path impossible. |
| Grid with dimensions 1x1 where grid[0][0] == 0 | Return 1, as the starting cell is also the ending cell, and the path length is 1. |
| No path exists (all paths are blocked) | BFS will exhaust all possible paths and return -1 when the target is not reached. |
| Start or end cell is blocked (grid[0][0] == 1 or grid[n-1][n-1] == 1) | Return -1 immediately if the start or end is blocked as no path can exist. |
| Integer overflow if grid size is extremely large. | Use appropriate data type (e.g., long) for path length to prevent overflow. |
| Grid with a very long path, potentially causing memory issues with the queue in BFS | The BFS approach handles this naturally as it explores the grid layer by layer, and we could handle OOM issues by using an iterative deepening approach. |