Serialize and Deserialize Binary Tree
HardSerialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
Clarification: The input/output format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
Example 1:
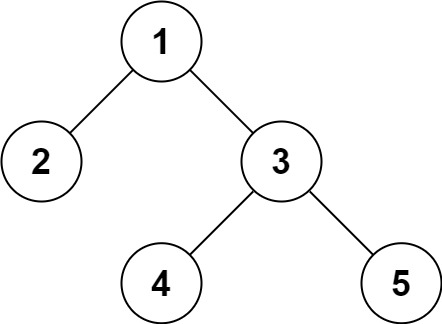
Input: root = [1,2,3,null,null,4,5] Output: [1,2,3,null,null,4,5]
Example 2:
Input: root = [] Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -1000 <= Node.val <= 1000
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What data type are the node values? And what is the range of possible values for the nodes in the tree?
- Can the tree be empty or contain a single node? What should the serialize function return in these cases?
- What format should the serialized string be in? Are there any specific delimiters or encoding methods you would prefer? (e.g., comma-separated values, pre-order traversal with 'null' markers)
- Does the binary tree have any specific properties, such as being a binary search tree, a complete binary tree, or a balanced tree?
- Is it possible for the tree to contain duplicate values, and if so, how should the serialization and deserialization handle them without ambiguity?
Brute Force Solution
Approach
The goal is to flatten a tree into a string so we can store it or send it somewhere, and then recreate the tree from that string later. The most basic way to do this is to try representing the tree level by level, recording each node's value.
Here's how the algorithm would work step-by-step:
- Start with the root of the tree.
- Write down the root's value to the string.
- Then, go to the next level and write down all the values of the nodes at that level from left to right.
- Repeat this process, level by level, writing down the values of all nodes at each level.
- If a node is empty, represent it with a special marker so we know it's missing when we rebuild the tree.
- This gives us a string representing the entire tree structure and its values.
- To rebuild the tree from the string, we reverse the process. We use the first value in the string as the root.
- Then, we use the next values in the string to create the children of the root, and so on, level by level.
- We continue this process, creating nodes and connecting them based on the order and values in the string, until we've reconstructed the entire tree, using the special marker to identify the nodes that do not exist.
Code Implementation
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class Solution:
def serialize(self, root):
if not root:
return ""
serialized_tree = []
queue = [root]
while queue:
current_node = queue.pop(0)
if current_node:
serialized_tree.append(str(current_node.value))
queue.append(current_node.left)
queue.append(current_node.right)
else:
serialized_tree.append("None")
return ','.join(serialized_tree)
def deserialize(self, data):
if not data:
return None
nodes = data.split(',')
root_value = nodes.pop(0)
# The root has to be handled since we are skipping it in the loop
if root_value == "None":
return None
root = TreeNode(int(root_value))
queue = [root]
# Process level by level, ensure order is correct
while queue and nodes:
current_node = queue.pop(0)
left_value = nodes.pop(0)
if left_value != "None":
left_node = TreeNode(int(left_value))
current_node.left = left_node
queue.append(left_node)
right_value = nodes.pop(0)
if right_value != "None":
right_node = TreeNode(int(right_value))
current_node.right = right_node
queue.append(right_node)
return rootBig(O) Analysis
Optimal Solution
Approach
We need to turn the tree into a string so we can save it and then recreate the tree from the string later. The best way is to walk through the tree in a specific order and record the value of each node, including special markers for empty spots so we know the tree's structure.
Here's how the algorithm would work step-by-step:
- Go through the tree in a pre-defined order: process the node, then the left side, then the right side.
- As you visit each node, write its value into a string. Use a special symbol like 'N' to represent a node that is missing (empty).
- Add a comma or another simple divider between each value and symbol so you can tell where each piece of information starts and ends.
- Once the whole tree is processed, you will have a single string that represents the tree.
- To recreate the tree from the string, first split the string back into individual values and symbols based on the divider.
- Then, use the same pre-defined order as before to reconstruct the tree. If you see a value, create a new node. If you see the special symbol, create an empty spot.
- Continue this process to create nodes, connect them to their left and right children, until you have the whole tree back.
- By using a consistent order and special symbols for missing nodes, you can accurately recreate the tree every time.
Code Implementation
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class Solution:
def serialize(self, root):
serialization_string = []
def preorder_traversal(node):
if not node:
serialization_string.append('N')
return
serialization_string.append(str(node.value))
preorder_traversal(node.left)
preorder_traversal(node.right)
preorder_traversal(root)
return ','.join(serialization_string)
def deserialize(self, data):
serialization_values = data.split(',')
self.index = 0
def build_tree():
# Use self.index to track progress during recursion
if self.index >= len(serialization_values):
return None
value = serialization_values[self.index]
self.index += 1
if value == 'N':
return None
node = TreeNode(int(value))
# Recursively build left and right subtrees
node.left = build_tree()
node.right = build_tree()
return node
# Need to call the recursive helper function
return build_tree()Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node (empty tree) | Serialize should return a special character like '#' or 'None', and deserialize should return null. |
| Tree with only a root node | Serialize should produce a simple string representation of the root's value followed by null indicators for left and right. |
| Completely unbalanced tree (left-skewed or right-skewed) | The solution should handle potentially deep recursion stacks for the serialization and deserialization. |
| Tree with duplicate values | The chosen serialization format must be able to distinguish nodes with the same value based on their position in the tree. |
| Large tree (memory constraints during serialization/deserialization) | Consider a space-efficient serialization format or streaming approach if the tree is extremely large to prevent memory exhaustion. |
| Very deep tree (stack overflow during recursive calls) | Iterative solutions (e.g., using a queue for deserialization) can prevent stack overflow errors. |
| Tree with values containing serialization delimiter | The serialization process must use a delimiter that does not appear within the node values themselves, or escape such delimiters if they are present. |
| Tree with null values interspersed within non-null values | The serialization must explicitly represent null nodes to maintain the tree structure during deserialization; otherwise, the wrong tree may result. |