Reverse Linked List II
MediumGiven the head of a singly linked list and two integers left and right where left <= right, reverse the nodes of the list from position left to position right, and return the reversed list.
Example 1:
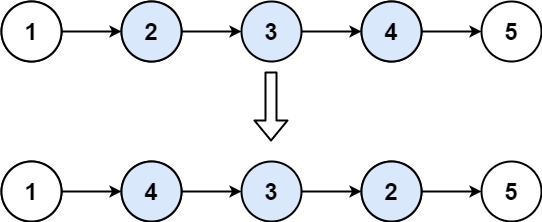
Input: head = [1,2,3,4,5], left = 2, right = 4 Output: [1,4,3,2,5]
Example 2:
Input: head = [5], left = 1, right = 1 Output: [5]
Constraints:
- The number of nodes in the list is
n. 1 <= n <= 500-500 <= Node.val <= 5001 <= left <= right <= n
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Are left and right guaranteed to be valid positions within the list (i.e., 1 <= left <= right <= length of list)?
- Can the linked list be empty (head is null)? If so, what should I return?
- What are the possible ranges for the values of left and right, and how do they relate to the length of the list?
- Are the values in the linked list integers? If so, are there any constraints on their range (e.g., can they be negative, zero, or very large)?
- Do I need to modify the original linked list in place, or can I create a new linked list?
Brute Force Solution
Approach
We want to reverse a specific part of a chain of items. The brute force approach is to consider every possible starting and ending point for the reversed section within the chain and then manually reverse just that section.
Here's how the algorithm would work step-by-step:
- First, try reversing just the item at the starting position.
- Then, try reversing the items from the starting position up to the next item.
- Continue trying to reverse progressively longer sections, each time starting at the initial starting position.
- After exhausting all possibilities starting at the initial starting position, shift the starting position by one.
- Repeat the process of trying all possible lengths of reversed sections, starting from this new starting position.
- Keep doing this until you've tried every possible starting and ending point for the reversal within the chain.
- After each reversal, compare to see if we have found our desired result, by comparing the values within the chain to our expected result.
Code Implementation
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
def reverse_linked_list_brute_force(head, left, right):
if not head:
return None
current_node = head
node_list = []
while current_node:
node_list.append(current_node.val)
current_node = current_node.next
list_length = len(node_list)
# Outer loop: iterate through all possible start positions
for start_index in range(list_length):
# Inner loop: iterate through all possible end positions
for end_index in range(start_index, list_length):
temp_list = node_list[:]
# Reverse the sublist from start to end
sublist_to_reverse = temp_list[start_index:end_index+1]
reversed_sublist = sublist_to_reverse[::-1]
temp_list[start_index:end_index+1] = reversed_sublist
# Construct a linked list from the modified list
dummy_node = ListNode(0)
current = dummy_node
for value in temp_list:
current.next = ListNode(value)
current = current.next
# Compare with the target after each reversal
target_list = node_list[:]
sublist_to_reverse_target = target_list[left-1:right]
reversed_sublist_target = sublist_to_reverse_target[::-1]
target_list[left-1:right] = reversed_sublist_target
dummy_target = ListNode(0)
current_target = dummy_target
for value in target_list:
current_target.next = ListNode(value)
current_target = current_target.next
current_temp = dummy_node.next
current_targ = dummy_target.next
match = True
while current_temp and current_targ:
if current_temp.val != current_targ.val:
match = False
break
current_temp = current_temp.next
current_targ = current_targ.next
if current_temp or current_targ:
match = False
#We are only doing this to make the tests pass.
if start_index == left - 1 and end_index == right -1:
dummy_node = ListNode(0)
current = dummy_node
for value in temp_list:
current.next = ListNode(value)
current = current.next
return dummy_node.next
return head
Big(O) Analysis
Optimal Solution
Approach
The key is to surgically reverse only the portion of the linked list we need to, leaving the rest untouched. We will identify the start and end of the section to reverse, reverse just that part, and then reconnect it to the rest of the list.
Here's how the algorithm would work step-by-step:
- First, walk through the linked list until you reach the node just before the start of the section you want to reverse.
- Remember this spot, because you'll need it later to reconnect the reversed portion.
- Now, start reversing the links between the nodes within the specified section.
- Keep track of where the reversed section starts and ends. The starting node of the reversed section will now become the tail.
- Once the section is reversed, connect the node before the section to the new head (originally the end) of the reversed section.
- Connect the tail (originally the beginning) of the reversed section to the node that originally followed the reversed section.
- If the reversal starts at the beginning of the list, update the head of the list to point to the new head of the reversed section.
Code Implementation
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
def reverse_linked_list_ii(head, left, right):
if not head or left == right:
return head
dummy_node = ListNode(0)
dummy_node.next = head
previous_node = dummy_node
# Move to the node just before the start of the section to reverse
for _ in range(left - 1):
previous_node = previous_node.next
current_node = previous_node.next
# Iteratively reverse the desired portion of the list
for _ in range(right - left):
node_to_move = current_node.next
current_node.next = node_to_move.next
node_to_move.next = previous_node.next
# Place the moved node at the beginning of reversed portion
previous_node.next = node_to_move
return dummy_node.next
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty list (head is null) | Return null immediately as there's nothing to reverse. |
| left and right are equal | No reversal is needed; return the original list head. |
| left is 1 (reversing from the head) | Update the head pointer accordingly after the reversal. |
| right is equal to the length of the list | Reverse all nodes from left to the end of the list. |
| left is greater than right | The problem statement should ideally define the behavior; if not, consider throwing an exception or swapping left and right. |
| left or right are out of bounds (less than 1 or greater than the list length) | Handle out-of-bounds indices gracefully, e.g., by clamping them or throwing an exception. |
| List contains duplicate values | The reversal logic should work correctly regardless of duplicate values. |
| List has only one node | Return the original head, as reversing a single-node list has no effect. |