Flood Fill
EasyYou are given an image represented by an m x n grid of integers image, where image[i][j] represents the pixel value of the image. You are also given three integers sr, sc, and color. Your task is to perform a flood fill on the image starting from the pixel image[sr][sc].
To perform a flood fill:
- Begin with the starting pixel and change its color to
color. - Perform the same process for each pixel that is directly adjacent (pixels that share a side with the original pixel, either horizontally or vertically) and shares the same color as the starting pixel.
- Keep repeating this process by checking neighboring pixels of the updated pixels and modifying their color if it matches the original color of the starting pixel.
- The process stops when there are no more adjacent pixels of the original color to update.
Return the modified image after performing the flood fill.
Example 1:
Input: image = [[1,1,1],[1,1,0],[1,0,1]], sr = 1, sc = 1, color = 2
Output: [[2,2,2],[2,2,0],[2,0,1]]
Explanation:
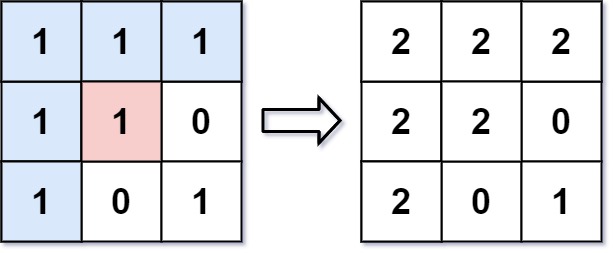
From the center of the image with position (sr, sc) = (1, 1) (i.e., the red pixel), all pixels connected by a path of the same color as the starting pixel (i.e., the blue pixels) are colored with the new color.
Note the bottom corner is not colored 2, because it is not horizontally or vertically connected to the starting pixel.
Example 2:
Input: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, color = 0
Output: [[0,0,0],[0,0,0]]
Explanation:
The starting pixel is already colored with 0, which is the same as the target color. Therefore, no changes are made to the image.
Constraints:
m == image.lengthn == image[i].length1 <= m, n <= 500 <= image[i][j], color < 2160 <= sr < m0 <= sc < n
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the image (rows and columns), and what is the data type used to represent the pixel colors? Can I assume it's always integers?
- What is the range of values for the pixel colors? Are negative color values possible?
- Is the starting row and column (sr, sc) always a valid coordinate within the image?
- If the starting pixel is already the target color, should the function still traverse and potentially modify the image, or should it return the original image without changes?
- Is the image guaranteed to be rectangular, or could there be rows with differing numbers of columns?
Brute Force Solution
Approach
The brute force method for flood fill is like trying to color an area by hand, one small piece at a time. We start at the given spot and check its neighbors, changing their color if they match the original color of the starting spot. We keep going until no more neighbors need to be changed.
Here's how the algorithm would work step-by-step:
- Look at the starting spot and remember its color.
- Check each spot right next to the starting spot.
- If a neighboring spot has the same color as the original starting spot, change its color to the new color.
- For each of those newly colored spots, check their neighbors too.
- If you find more neighbors with the original starting color, change their color to the new color as well.
- Keep repeating this process of checking neighbors and changing colors until there are no more spots that need changing around all the spots you've already colored.
Code Implementation
def flood_fill(image, start_row, start_column, new_color):
original_color = image[start_row][start_column]
# If the starting color is already the new color, there is nothing to do.
if original_color == new_color:
return image
rows = len(image)
columns = len(image[0])
pixels_to_process = [(start_row, start_column)]
while pixels_to_process:
current_row, current_column = pixels_to_process.pop(0)
# Only process the pixel if it's within bounds and matches the original color.
if 0 <= current_row < rows and 0 <= current_column < columns and image[current_row][current_column] == original_color:
image[current_row][current_column] = new_color
# Add neighboring pixels to process.
pixels_to_process.append((current_row + 1, current_column))
pixels_to_process.append((current_row - 1, current_column))
pixels_to_process.append((current_row, current_column + 1))
pixels_to_process.append((current_row, current_column - 1))
return imageBig(O) Analysis
Optimal Solution
Approach
The Flood Fill problem is like coloring a connected area in an image. We start at a given point and change the color of all adjacent points that have the same original color, continuing until we've colored the entire connected region. The trick is to explore outwards in a systematic way.
Here's how the algorithm would work step-by-step:
- Start at the specific point where the coloring should begin.
- Check the color of the starting point. This is the original color that will be replaced.
- Change the color of the starting point to the new color.
- Look at the points directly above, below, to the left, and to the right of the current point.
- For each of these neighboring points, if its color matches the original color, then change its color to the new color and repeat this process (steps 4 and 5) for that point.
- Continue this process of checking neighbors and changing colors until you've reached the edges of the connected region, meaning there are no more adjacent points with the original color to change. It's like the new color is 'flooding' outwards.
Code Implementation
def flood_fill(image, start_row, start_column, new_color):
rows = len(image)
columns = len(image[0])
original_color = image[start_row][start_column]
# If the starting color is already the new color, there's nothing to do.
if original_color == new_color:
return image
def fill_recursive(row, column):
# Base case: check boundaries and color.
if row < 0 or row >= rows or column < 0 or column >= columns or image[row][column] != original_color:
return
# Set the current pixel to the new color.
image[row][column] = new_color
# Recursively fill adjacent pixels.
fill_recursive(row + 1, column)
fill_recursive(row - 1, column)
fill_recursive(row, column + 1)
fill_recursive(row, column - 1)
# Initiate flood fill from the starting pixel
fill_recursive(start_row, start_column)
return imageBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty image input | Return the original image if it's null or empty, as there's nothing to flood fill. |
| Starting pixel outside image bounds | Check if the starting row and column are within the image dimensions and return the original image if outside. |
| Image with only one pixel | If the image has only one pixel, change its color to the new color and return. |
| Original color is the same as the new color | Return the original image immediately since no changes are required. |
| Stack Overflow with large images or recursive implementations | Favor an iterative (queue-based) approach over a recursive one to avoid stack overflow errors with large images. |
| Integer overflow when calculating row/column indices | Ensure that row and column calculations do not result in integer overflows, particularly if the image dimensions are very large by using appropriate data types. |
| Very large image dimensions leading to memory issues | Be mindful of memory usage with extremely large images; consider processing the image in chunks or using techniques to optimize memory allocation. |
| Image with all pixels already the target color adjacent to the starting pixel | The algorithm should still terminate correctly, changing connected pixels as it goes, but ultimately changing none since they are already the target color. |