Detect Cycles in 2D Grid

Medium

Google

1 view

Topics:

ArraysStringsGraphsRecursion

Given a 2D array of characters grid of size m x n, you need to find if there exists any cycle consisting of the same value in grid.

A cycle is a path of length 4 or more in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the same value of the current cell.

Also, you cannot move to the cell that you visited in your last move. For example, the cycle (1, 1) -> (1, 2) -> (1, 1) is invalid because from (1, 2) we visited (1, 1) which was the last visited cell.

Return true if any cycle of the same value exists in grid, otherwise, return false.

Example 1:

Input: grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
Output: true
Explanation: There are two valid cycles shown in different colors in the image below:

Example 2:

Input: grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
Output: true
Explanation: There is only one valid cycle highlighted in the image below:

Example 3:

Input: grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
Output: false

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 500
grid consists only of lowercase English letters.

Detect Cycles in 2D Grid

Medium

Google

1 view

Topics:

ArraysStringsGraphsRecursion

Given a 2D array of characters grid of size m x n, you need to find if there exists any cycle consisting of the same value in grid.

A cycle is a path of length 4 or more in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the same value of the current cell.

Also, you cannot move to the cell that you visited in your last move. For example, the cycle (1, 1) -> (1, 2) -> (1, 1) is invalid because from (1, 2) we visited (1, 1) which was the last visited cell.

Return true if any cycle of the same value exists in grid, otherwise, return false.

Example 1:

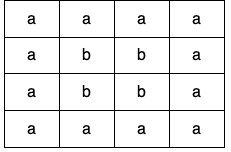
Input: grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
Output: true
Explanation: There are two valid cycles shown in different colors in the image below: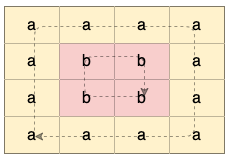

Example 2:

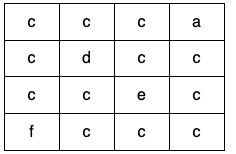
Input: grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
Output: true
Explanation: There is only one valid cycle highlighted in the image below: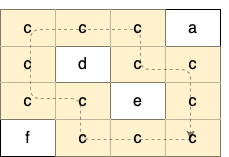

Example 3:

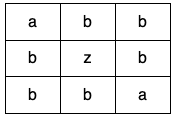
Input: grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
Output: false

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 500
grid consists only of lowercase English letters.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the possible values of the characters in the grid, and are they limited to a specific set (e.g., lowercase English letters)?
How is a cycle defined? Specifically, can a cycle include revisiting a cell immediately after leaving it (i.e., moving back and forth between two adjacent cells)?
What should I return if no cycle is found in the grid? Should I return `false`, `null`, or throw an exception?
Is the grid guaranteed to be rectangular (i.e., all rows have the same number of columns)?
What is the maximum size of the grid (number of rows and columns) that the input can have?

Brute Force Solution

Approach

The brute force approach to finding cycles in a grid involves exploring every possible path. We start at a cell and check all potential paths from that cell until we either find a cycle or exhaust all possibilities. This ensures we don't miss any possible cycles, but it can be slow.

Here's how the algorithm would work step-by-step:

Start at the first cell in the grid.
Consider all possible directions to move from this cell: up, down, left, and right.
Pick one direction and move to the next cell. Keep track of where you've already been to avoid immediately going back.
From this new cell, again consider all possible directions (except the one you just came from) and move to another cell, continuing to remember your path.
Repeat this process, exploring each path as far as you can, until one of two things happens: either you come back to a cell you've already visited (and the new cell has the same value as the starting cell), which means you've found a cycle, or you reach a dead end where you can't move without revisiting a cell or going out of bounds.
If you find a cycle, you're done! If you reach a dead end, backtrack. Go back to the last cell where you had a choice of directions and try a different direction.
If you've tried all directions from the first cell and haven't found a cycle, move on to the next cell in the grid and repeat the entire process from there.
Keep doing this for every cell in the grid until you either find a cycle or you've checked every single cell and exhausted all possible paths.

Code Implementation

def detect_cycles_in_2d_grid(grid):
    rows = len(grid)
    cols = len(grid[0])
    visited = [[False] * cols for _ in range(rows)]

    def explore_paths(row, col, parent_row, parent_col, start_row, start_col):
        if row < 0 or row >= rows or col < 0 or col >= cols:
            return False

        if grid[row][col] != grid[start_row][start_col]:
            return False

        if visited[row][col]:
            return True

        visited[row][col] = True

        # Explore all possible paths
        directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]

        for delta_row, delta_col in directions:
            new_row = row + delta_row
            new_col = col + delta_col

            # Avoid going back to the parent cell
            if new_row == parent_row and new_col == parent_col:
                continue

            if explore_paths(new_row, new_col, row, col, start_row, start_col):
                return True

        return False

    for row in range(rows):
        for col in range(cols):
            # Reset visited for each starting cell
            visited = [[False] * cols for _ in range(rows)]

            # Need to check if this cell is the start of a cycle
            if explore_paths(row, col, -1, -1, row, col):
                return True

    # No cycles were found in the grid
    return False

Big(O) Analysis

Time Complexity

O(m*n*4^(m*n)) – The brute force approach explores all possible paths starting from each cell in the m x n grid. From each cell, there are potentially 4 directions to move (up, down, left, right). The longest possible path without revisiting a cell has a length proportional to m*n. In the worst case, we explore all paths from each of the m*n starting cells, with each path having up to 4 possible directions at each step. This results in a time complexity of O(m*n*4^(m*n)), where m*n is the number of cells and 4^(m*n) represents the exponential growth of possible paths.

Space Complexity

O(N) – The algorithm utilizes a visited matrix to keep track of visited cells during the depth-first search, where N is the total number of cells in the grid (rows * cols). In the worst-case scenario, the algorithm might explore a significant portion of the grid before finding a cycle or exhausting all paths. Additionally, the recursion stack can grow to a depth proportional to the number of cells, N, in a long path. Therefore, the auxiliary space used by the visited matrix and the recursion stack is proportional to N, leading to a space complexity of O(N).

Optimal Solution

Approach

The problem asks us to find a cycle in a grid where movements are only allowed to adjacent cells with the same value. The optimal approach involves exploring the grid systematically, marking visited locations and checking for revisits that form a cycle.

Here's how the algorithm would work step-by-step:

Start at any cell in the grid.
Explore adjacent cells that have the same value as the current cell.
Keep track of where you've been; mark each visited cell as 'seen'.
When moving to a new adjacent cell, remember where you came from.
If you reach a cell that has already been 'seen', but it's NOT the cell you came from in the previous step, then you've found a cycle.
If you explore all possible paths from a starting cell without finding a cycle, move on to the next unvisited cell and repeat the process.
If you've checked every cell and found no cycles, then the grid does not contain any cycles.

Code Implementation

def detect_cycles_in_grid(grid):
    rows = len(grid)
    cols = len(grid[0])
    visited = [[False] * cols for _ in range(rows)]

    def depth_first_search(row, col, parent_row, parent_col, cell_value):
        visited[row][col] = True

        # Explore all 4 adjacent cells
        for delta_row, delta_col in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
            new_row = row + delta_row
            new_col = col + delta_col

            #Bounds check for new coordinates
            if 0 <= new_row < rows and 0 <= new_col < cols and grid[new_row][new_col] == cell_value:

                # Cycle detected!
                if visited[new_row][new_col] and (new_row != parent_row or new_col != parent_col):
                    return True

                # Recursively explore the adjacent cell
                if not visited[new_row][new_col]:
                    if depth_first_search(new_row, new_col, row, col, cell_value):
                        return True

        return False

    # Iterate through each cell in the grid
    for row_index in range(rows):
        for col_index in range(cols):
            # Only explore unvisited cells
            if not visited[row_index][col_index]:

                #Begin searching for cycle from current cell.
                if depth_first_search(row_index, col_index, -1, -1, grid[row_index][col_index]):
                    return True

    #No cycles were found in the grid
    return False

Big(O) Analysis

Time Complexity

O(m * n) – We perform a Depth-First Search (DFS) traversal of the grid. In the worst case, we might need to visit each cell in the grid. Each cell can be visited only once during a single DFS call because we mark visited cells. The grid has dimensions m x n, where m is the number of rows and n is the number of columns. Therefore, the worst-case time complexity is proportional to the number of cells in the grid, leading to O(m * n).

Space Complexity

O(N) – The algorithm utilizes a 'seen' matrix to keep track of visited cells during the exploration of the grid, where N is the total number of cells in the grid (rows * cols). The size of this matrix scales linearly with the number of cells, directly impacting the auxiliary space. Additionally, the depth of the recursion stack during the Depth-First Search (DFS) can, in the worst-case, reach all cells in the grid. Therefore, the algorithm uses O(N) auxiliary space.

Edge Cases

Case	How to Handle
Null or empty grid	Return false immediately, as there can be no cycles.
1x1 grid	Return false, as a cycle requires at least two cells.
2x2 grid with all same values	Detect the simple cycle consisting of all four cells.
Grid with a single long cycle	The DFS or BFS should traverse the entire cycle and identify it.
Grid with multiple disjoint cycles	The algorithm must iterate through all unvisited cells to find all cycles.
Large grid causing stack overflow with DFS	Consider using BFS or iterative DFS to avoid stack overflow.
Grid with values at integer boundaries (min/max int)	Ensure no integer overflow occurs during comparisons or calculations of distances, using appropriate data types.
Cycle of length 1 (a cell connected to itself), should be treated as not a valid cycle as the problem doesn't allow it.	Ensure the DFS/BFS only considers cycles with a length of at least 4.