Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree

Hard

Google

5 views

Topics:

GraphsGreedy Algorithms

Given a weighted undirected connected graph with n vertices numbered from 0 to n - 1, and an array edges where edges[i] = [a_i, b_i, weight_i] represents a bidirectional and weighted edge between nodes a_i and b_i. A minimum spanning tree (MST) is a subset of the graph's edges that connects all vertices without cycles and with the minimum possible total edge weight.

Find all the critical and pseudo-critical edges in the given graph's minimum spanning tree (MST). An MST edge whose deletion from the graph would cause the MST weight to increase is called a critical edge. On the other hand, a pseudo-critical edge is that which can appear in some MSTs but not all.

Note that you can return the indices of the edges in any order.

Example 1:

Input: n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
Output: [[0,1],[2,3,4,5]]
Explanation: The figure above describes the graph.
The following figure shows all the possible MSTs:

Notice that the two edges 0 and 1 appear in all MSTs, therefore they are critical edges, so we return them in the first list of the output.
The edges 2, 3, 4, and 5 are only part of some MSTs, therefore they are considered pseudo-critical edges. We add them to the second list of the output.

Example 2:

Input: n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
Output: [[],[0,1,2,3]]
Explanation: We can observe that since all 4 edges have equal weight, choosing any 3 edges from the given 4 will yield an MST. Therefore all 4 edges are pseudo-critical.

Constraints:

2 <= n <= 100
1 <= edges.length <= min(200, n * (n - 1) / 2)
edges[i].length == 3
0 <= a_i < b_i < n
1 <= weight_i <= 1000
All pairs (a_i, b_i) are distinct.

Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree

Hard

Google

5 views

Topics:

GraphsGreedy Algorithms

Given a weighted undirected connected graph with n vertices numbered from 0 to n - 1, and an array edges where edges[i] = [a_i, b_i, weight_i] represents a bidirectional and weighted edge between nodes a_i and b_i. A minimum spanning tree (MST) is a subset of the graph's edges that connects all vertices without cycles and with the minimum possible total edge weight.

Find all the critical and pseudo-critical edges in the given graph's minimum spanning tree (MST). An MST edge whose deletion from the graph would cause the MST weight to increase is called a critical edge. On the other hand, a pseudo-critical edge is that which can appear in some MSTs but not all.

Note that you can return the indices of the edges in any order.

Example 1:

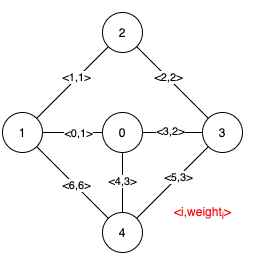
Input: n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
Output: [[0,1],[2,3,4,5]]
Explanation: The figure above describes the graph.
The following figure shows all the possible MSTs:

Notice that the two edges 0 and 1 appear in all MSTs, therefore they are critical edges, so we return them in the first list of the output.
The edges 2, 3, 4, and 5 are only part of some MSTs, therefore they are considered pseudo-critical edges. We add them to the second list of the output.

Example 2:

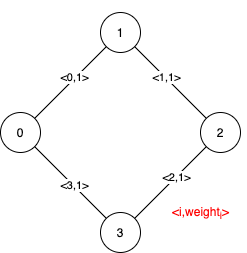
Input: n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
Output: [[],[0,1,2,3]]
Explanation: We can observe that since all 4 edges have equal weight, choosing any 3 edges from the given 4 will yield an MST. Therefore all 4 edges are pseudo-critical.

Constraints:

2 <= n <= 100
1 <= edges.length <= min(200, n * (n - 1) / 2)
edges[i].length == 3
0 <= a_i < b_i < n
1 <= weight_i <= 1000
All pairs (a_i, b_i) are distinct.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the number of nodes `n` and edges in the graph `edges`? Specifically, what are the maximum values for `n` and the length of `edges`?
Can edge weights be negative, zero, or floating-point numbers? What is the range of possible edge weights?
If multiple minimum spanning trees (MSTs) exist, should the critical and pseudo-critical edges be consistent across *all* possible MSTs, or is it sufficient to identify them based on *one* valid MST?
Is the input graph guaranteed to be connected? If not, how should I handle disconnected components?
Can there be duplicate edges (i.e., multiple edges connecting the same two nodes with the same weight)? If so, how should I handle them in determining critical/pseudo-critical edges?

Brute Force Solution

Approach

We're trying to find which connections between cities are absolutely necessary for the cheapest road network, and which are just helpful but not crucial. The brute force approach involves exhaustively testing each connection's importance by trying out every possible scenario for the road network with and without that connection.

Here's how the algorithm would work step-by-step:

First, calculate the cost of the absolute cheapest road network connecting all cities without any restrictions. Think of this as our baseline cost.
Now, for each individual connection, do the following:
Try forcing that specific connection to be part of the road network. Recalculate the cheapest road network, but this time, make sure that particular connection is definitely included. If this new cheapest network costs more than our baseline, then that connection is absolutely necessary. We call those connections 'critical'.
Next, again for that same individual connection, try forbidding it from being part of the road network. Recalculate the cheapest road network, but this time, completely ignore that connection. If the new cheapest network costs more than our baseline, then that connection is potentially 'pseudo-critical'. However, it could actually be 'critical' if there are multiple cheapest MSTs.
After testing every single connection in this way, go through each connection that was marked as 'potentially pseudo-critical'. If forcing that connection to be present results in a network cost equal to our initial baseline cost, then it actually 'pseudo-critical'. Otherwise, if the cost is higher, then it is actually a 'critical' connection.

Code Implementation

def find_critical_and_pseudo_critical_edges(number_of_nodes, edges):    number_of_edges = len(edges)
    minimum_spanning_tree_cost = calculate_mst_cost(number_of_nodes, edges, None, None)

    critical_edges = []
    pseudo_critical_edges = []

    for edge_index in range(number_of_edges):
        # Test each edge to find critical and pseudo-critical edges
        edge = edges[edge_index]
        
        included_edge = edge
        excluded_edge_index = edge_index

        mst_cost_with_edge_forced = calculate_mst_cost(
            number_of_nodes, edges, included_edge, None
        )

        if mst_cost_with_edge_forced > minimum_spanning_tree_cost:
            # If cost increases, the edge is critical
            critical_edges.append(edge_index)

            continue

        mst_cost_with_edge_excluded = calculate_mst_cost(
            number_of_nodes, edges, None, excluded_edge_index
        )

        if mst_cost_with_edge_excluded > minimum_spanning_tree_cost:
            # If cost increases, the edge is potentially pseudo-critical
            pseudo_critical_edges.append(edge_index)

    # Refine pseudo-critical edges
    refined_pseudo_critical_edges = []
    for edge_index in pseudo_critical_edges:
        included_edge = edges[edge_index]
        
        mst_cost_with_edge_forced = calculate_mst_cost(
            number_of_nodes, edges, included_edge, None
        )

        if mst_cost_with_edge_forced == minimum_spanning_tree_cost:
            # It really is pseudo-critical
            refined_pseudo_critical_edges.append(edge_index)

    return [critical_edges, refined_pseudo_critical_edges]

def calculate_mst_cost(number_of_nodes, edges, included_edge, excluded_edge_index):
    parent = list(range(number_of_nodes))
    
    def find(node):
        if parent[node] != node:
            parent[node] = find(parent[node])
        return parent[node]

    def union(node1, node2):
        root1 = find(node1)
        root2 = find(node2)
        parent[root1] = root2

    cost = 0
    edges_used = 0

    # Force inclusion of an edge
    if included_edge:
        node1, node2, weight = included_edge
        if find(node1) != find(node2):
            union(node1, node2)
            cost += weight
            edges_used += 1

    sorted_edges = sorted(enumerate(edges), key=lambda x: x[1][2])

    for index, (node1, node2, weight) in map(lambda x: (x[0],x[1]), sorted_edges):
        # Exclude an edge
        if index == excluded_edge_index:
            continue
        
        if find(node1) != find(node2):
            # Only include edge if it connects different components
            union(node1, node2)
            cost += weight
            edges_used += 1

        if edges_used == number_of_nodes - 1:
            # Early termination condition
            break
    
    if edges_used != number_of_nodes - 1:
        # Not all nodes are connected
        return float('inf')
    
    return cost

Big(O) Analysis

Time Complexity

O(m * (m + n log n)) – The algorithm iterates through each of the 'm' edges in the graph. For each edge, it calculates the Minimum Spanning Tree (MST) twice: once forcing the edge to be included and once excluding it. Calculating the MST using Kruskal's or Prim's algorithm typically takes O(n log n) or O(m log n) time where n is the number of nodes and m is the number of edges. In the worst-case scenario, calculating the MST might take O(m) (if the graph is very dense, we may need to check all possible edges). The critical part is repeating this MST computation m times. Thus, the overall time complexity is O(m * (m + n log n)).

Space Complexity

O(E) – The algorithm calculates the Minimum Spanning Tree (MST) multiple times, each time potentially storing the edges of the MST, where E is the number of edges. The Kruskal's or Prim's algorithm used to compute the MST internally may also utilize data structures like Union-Find, whose space complexity is related to the number of vertices (V), or an adjacency list/matrix. In the worst-case scenario when the graph is dense, E can be close to V^2, but we consider the space used to represent the MST after each computation and auxiliary data structures used, each needing at most O(E) space. The final critical and pseudo-critical lists themselves take O(E) space.

Optimal Solution

Approach

We need to find edges that are either crucial for forming the cheapest connection between points or are almost crucial. We achieve this by finding the minimum cost to connect the points and then re-evaluating each connection's importance individually.

Here's how the algorithm would work step-by-step:

First, find the absolute cheapest way to connect all the points together. Note down the total cost of this connection.
Now, consider each connection individually. Force this connection to be part of the solution and find the cheapest way to connect all the points *including* this forced connection. If this new connection's cost is higher than our initial cheapest cost, then this connection is crucial.
Next, consider each connection individually again, but this time *forbid* the connection from being used at all. Find the cheapest way to connect all the points *without* this forbidden connection. If the cost to connect all the points is now *higher* than our original cheapest cost and if forcing this connection resulted in the same cost, then this connection is almost crucial.

Code Implementation

def find_critical_and_pseudo_critical_edges(
    number_of_nodes: int, edges: list[list[int]]
) -> list[list[int]]:
    number_of_edges = len(edges)
    minimum_spanning_tree_weight = get_mst_weight(number_of_nodes, edges, -1, -1)

    critical_edges = []
    pseudo_critical_edges = []

    for edge_index in range(number_of_edges):
        # Test each edge for critical property.
        forced_mst_weight = get_mst_weight(
            number_of_nodes, edges, edge_index, -1
        )
        if forced_mst_weight > minimum_spanning_tree_weight:
            critical_edges.append(edge_index)
        else:
            # Test each edge for pseudo-critical property.
            forbidden_mst_weight = get_mst_weight(
                number_of_nodes, edges, -1, edge_index
            )
            if (
                forbidden_mst_weight > minimum_spanning_tree_weight
                and forced_mst_weight == minimum_spanning_tree_weight
            ):
                pseudo_critical_edges.append(edge_index)

    return [critical_edges, pseudo_critical_edges]

def get_mst_weight(
    number_of_nodes: int, edges: list[list[int]], force_edge_index: int, skip_edge_index: int
) -> int:
    parent = list(range(number_of_nodes))
    mst_weight = 0
    edge_count = 0

    def find(node_index: int) -> int:
        if parent[node_index] != node_index:
            parent[node_index] = find(parent[node_index])
        return parent[node_index]

    def union(node_index1: int, node_index2: int) -> None:
        root_node_index1 = find(node_index1)
        root_node_index2 = find(node_index2)
        if root_node_index1 != root_node_index2:
            parent[root_node_index1] = root_node_index2

    # Force the edge if specified.
    if force_edge_index != -1:
        node_index1, node_index2, weight = edges[force_edge_index][:3]
        union(node_index1, node_index2)
        mst_weight += weight
        edge_count += 1

    # Sort edges by weight.
    sorted_edges = sorted(
        [(weight, node_index1, node_index2, edge_index)
         for edge_index, (node_index1, node_index2, weight) in enumerate(edges)],
        key=lambda x: x[0],
    )

    # Iterate through sorted edges to build MST.
    for weight, node_index1, node_index2, edge_index in sorted_edges:
        if edge_index == skip_edge_index:
            continue

        if find(node_index1) != find(node_index2):
            # Add edge to MST if it connects disjoint sets.
            union(node_index1, node_index2)
            mst_weight += weight
            edge_count += 1

    # Check if all nodes are connected.
    if edge_count != number_of_nodes - 1:
        return float('inf')

    return mst_weight

Big(O) Analysis

Time Complexity

O(E * (E + V * log(V))) – The algorithm iterates through each edge in the input list of edges E. For each edge, the algorithm performs Kruskal's algorithm twice: once forcing the edge to be included in the MST and once forbidding the edge from being included. Kruskal's algorithm, using a disjoint set union data structure, has a time complexity of O(E + V * log(V)), where V is the number of vertices. Since Kruskal's algorithm is run for each edge in E, the total time complexity is O(E * (E + V * log(V))). This can be further elaborated based on specific disjoint set union optimizations.

Space Complexity

O(E) – The algorithm primarily utilizes Kruskal's algorithm (implicitly) multiple times, both when finding the initial MST and when forcing/excluding edges. Kruskal's algorithm typically employs a Disjoint Set Union (DSU) data structure to track connected components. The DSU's space complexity is proportional to the number of vertices, V, which is related to the number of edges, E. Furthermore, when forcing or forbidding edges, temporary data structures may be created to store the modified edge lists, whose size is dependent on E. Thus, the auxiliary space is largely determined by storing these temporary data structures and the DSU, leading to a space complexity of O(E).

Edge Cases

Case	How to Handle
Empty graph (n=0) or no edges	Return empty lists for both critical and pseudo-critical edges since there is no MST.
Graph with only one node (n=1)	Return empty lists, as a single node cannot form a minimum spanning tree.
Graph is already a tree (no cycles)	All edges are critical since removing any would disconnect the graph.
Edge weights are negative	Kruskal's and Prim's algorithms, which are typically used for MST, work correctly with negative edge weights.
Edge weights are zero	Zero-weight edges might create multiple MSTs; the solution needs to ensure all such edges are correctly categorized as critical or pseudo-critical.
Multiple edges with the same weight exist, potentially leading to different MSTs.	The algorithm should consider all possible MSTs formed by edges of equal weight and identify edges that are critical across all such MSTs and pseudo-critical in at least one.
The graph is not connected (no MST exists)	Return empty lists for both critical and pseudo-critical edges if no MST can be formed.
Integer overflow when calculating the MST weight with large edge weights or large number of edges.	Use long data type to store MST weight to prevent potential integer overflow issues.