Maximum Number of Visible Points

Hard

Google

3 views

Topics:

ArraysTwo PointersGreedy Algorithms

You are given an array points, an integer angle, and your location, where location = [pos_x, pos_y] and points[i] = [x_i, y_i] both denote integral coordinates on the X-Y plane.

Initially, you are facing directly east from your position. You cannot move from your position, but you can rotate. In other words, pos_x and pos_y cannot be changed. Your field of view in degrees is represented by angle, determining how wide you can see from any given view direction. Let d be the amount in degrees that you rotate counterclockwise. Then, your field of view is the inclusive range of angles [d - angle/2, d + angle/2].

You can see some set of points if, for each point, the angle formed by the point, your position, and the immediate east direction from your position is in your field of view.

There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.

Return the maximum number of points you can see.

Example 1:

Input: points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
Output: 3
Explanation: The shaded region represents your field of view. All points can be made visible in your field of view, including [3,3] even though [2,2] is in front and in the same line of sight.

Example 2:

Input: points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
Output: 4
Explanation: All points can be made visible in your field of view, including the one at your location.

Example 3:

Input: points = [[1,0],[2,1]], angle = 13, location = [1,1]
Output: 1
Explanation: You can only see one of the two points, as shown above.

Constraints:

1 <= points.length <= 10⁵
points[i].length == 2
location.length == 2
0 <= angle < 360
0 <= pos_x, pos_y, x_i, y_i <= 100

Maximum Number of Visible Points

Hard

Google

3 views

Topics:

ArraysTwo PointersGreedy Algorithms

You are given an array points, an integer angle, and your location, where location = [pos_x, pos_y] and points[i] = [x_i, y_i] both denote integral coordinates on the X-Y plane.

Initially, you are facing directly east from your position. You cannot move from your position, but you can rotate. In other words, pos_x and pos_y cannot be changed. Your field of view in degrees is represented by angle, determining how wide you can see from any given view direction. Let d be the amount in degrees that you rotate counterclockwise. Then, your field of view is the inclusive range of angles [d - angle/2, d + angle/2].

You can see some set of points if, for each point, the angle formed by the point, your position, and the immediate east direction from your position is in your field of view.

There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.

Return the maximum number of points you can see.

Example 1:

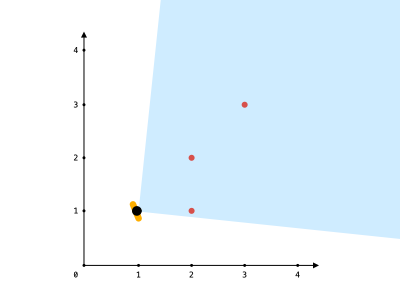
Input: points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
Output: 3
Explanation: The shaded region represents your field of view. All points can be made visible in your field of view, including [3,3] even though [2,2] is in front and in the same line of sight.

Example 2:

Input: points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
Output: 4
Explanation: All points can be made visible in your field of view, including the one at your location.

Example 3:

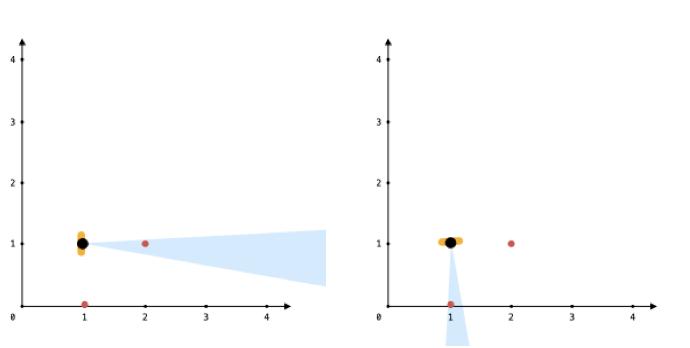
Input: points = [[1,0],[2,1]], angle = 13, location = [1,1]
Output: 1
Explanation: You can only see one of the two points, as shown above.

Constraints:

1 <= points.length <= 10⁵
points[i].length == 2
location.length == 2
0 <= angle < 360
0 <= pos_x, pos_y, x_i, y_i <= 100

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the number of points and the range of their x and y coordinates?
Can the angle between two points be zero? If so, should that be included as visible?
If there are multiple points at the same location as the location of the observer, how should those be handled? Are they always considered visible?
Is the angle of view given in degrees or radians, and what are the possible values for the angle?
If there are no visible points within the field of view, what should be returned?

Brute Force Solution

Approach

The brute force approach to finding the maximum visible points is all about trying out every possible combination of points and checking which one gives us the best view. It’s like manually looking at every possibility to find the best one, even if it takes a long time. We are trying out all the possible angles and see which one contains the most points.

Here's how the algorithm would work step-by-step:

Imagine standing at your location and picking two points that will define the edges of your viewing angle. These points will be the start and end points of your field of vision.
Now, consider every possible pair of points. You'll try using each of these pairs as the boundaries of your viewing angle.
For each chosen pair of points, count how many of the remaining points are within the viewing angle created by those two points.
Remember to also count the points that are exactly at your location, since these are always visible.
Keep track of the maximum number of points that you can see for any of the angles you've tried.
After trying all possible pairs of points as the boundaries of your view, the highest number of points you saw within any of those views is your answer.

Code Implementation

import math

def maximum_number_of_visible_points_brute_force(points, angle_degrees, location):
    maximum_visible_points = 0
    same_location_points_count = 0

    for point in points:
        if point[0] == location[0] and point[1] == location[1]:
            same_location_points_count += 1

    for first_point_index in range(len(points)): 
        for second_point_index in range(first_point_index + 1, len(points)): 
            # Consider every pair of points as the angle boundaries.
            angle1 = math.atan2(points[first_point_index][1] - location[1], points[first_point_index][0] - location[0]) * 180 / math.pi
            angle2 = math.atan2(points[second_point_index][1] - location[1], points[second_point_index][0] - location[0]) * 180 / math.pi
            
            viewing_angle = abs(angle1 - angle2)
            viewing_angle = min(viewing_angle, 360 - viewing_angle)

            if viewing_angle > angle_degrees:
                continue
            
            visible_points_count = 0
            # Count points within the calculated viewing angle
            for third_point_index in range(len(points)): 
                if third_point_index == first_point_index or third_point_index == second_point_index:
                    continue

                angle3 = math.atan2(points[third_point_index][1] - location[1], points[third_point_index][0] - location[0]) * 180 / math.pi

                viewing_angle_with_first = abs(angle1 - angle3)
                viewing_angle_with_first = min(viewing_angle_with_first, 360 - viewing_angle_with_first)

                viewing_angle_with_second = abs(angle2 - angle3)
                viewing_angle_with_second = min(viewing_angle_with_second, 360 - viewing_angle_with_second)

                # Check if the third point is inside the viewing angle
                if viewing_angle_with_first + viewing_angle_with_second <= viewing_angle + 1e-6:
                    visible_points_count += 1

            maximum_visible_points = max(maximum_visible_points, visible_points_count + 2)

    return maximum_visible_points + same_location_points_count

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n³) – The brute force approach iterates through all possible pairs of points to define the viewing angle. This involves a nested loop, resulting in approximately n * (n-1) / 2 pairs. For each pair, we then iterate through the remaining points to check if they fall within the viewing angle defined by the pair, which takes O(n) time. Therefore, the overall time complexity is approximately (n * (n-1) / 2) * n, which simplifies to O(n³).

Space Complexity

O(1) – The brute force approach, as described, iterates through pairs of points without creating any auxiliary data structures that scale with the number of points, N. It only needs a few variables to keep track of the indices of the points that define the viewing angle and to store the maximum count found so far. Therefore, the space complexity is constant.

Optimal Solution

Approach

The key is to sort points by their angle relative to your location. Then, we use a sliding window approach to find the maximum number of points within your field of view, handling cases where points wrap around (like going past 360 degrees).

Here's how the algorithm would work step-by-step:

First, calculate the angle of each point relative to your location.
Sort all the angles in ascending order. This helps in finding points that are close together angularly.
To handle the circular nature of angles (0 degrees is the same as 360 degrees), duplicate the sorted angles, adding 360 degrees to each of the duplicates. This lets us easily find points near the 'end' that should be counted with points near the 'beginning'.
Use a sliding window. Keep track of the points within your field of view.
As you move the window, expand it to include more points until the angle difference between the start and end of the window exceeds your field of view.
When the angle difference is too large, shrink the window from the left until the angle difference is within your field of view again.
Keep track of the maximum number of points found within the window at any time.
Count the number of points that are exactly at your location, because the viewing angle doesn't matter for them.
Add the number of points at your location to the maximum number of visible points found by the sliding window. This is your final answer.

Code Implementation

import math

def maximum_number_of_visible_points(points, angle, location):
    same_location_points = 0
    angles = []
    for point in points:
        x_difference = point[0] - location[0]
        y_difference = point[1] - location[1]
        if x_difference == 0 and y_difference == 0:
            same_location_points += 1
        else:
            angle_degrees = math.atan2(y_difference, x_difference) * 180 / math.pi
            angles.append(angle_degrees if angle_degrees >= 0 else angle_degrees + 360)

    angles.sort()

    # Handle circular nature by duplicating angles
    extended_angles = angles + [ang + 360 for ang in angles]

    max_points = 0
    window_start = 0
    window_end = 0
    while window_end < len(extended_angles):
        # Expand window until angle exceeds field of view
        while window_end < len(extended_angles) and \
                extended_angles[window_end] - extended_angles[window_start] <= angle:
            window_end += 1

        # Update the maximum number of points
        max_points = max(max_points, window_end - window_start)

        # Shrink window from the left
        window_start += 1

    # Points at the same location are always visible
    return max_points + same_location_points

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n log n) – Calculating the angle for each of the n points relative to the location takes O(n) time. Sorting the angles takes O(n log n) time. Duplicating the sorted angles also takes O(n) time. The sliding window approach iterates through the 2n angles in the extended array, performing constant time operations for each angle to expand and shrink the window, resulting in O(n) time. Therefore, the dominant factor is the sorting step, giving a total time complexity of O(n log n).

Space Complexity

O(N) – The space complexity is primarily determined by the creation of the 'angles' list which stores the calculated angle for each of the N points. Additionally, the 'angles' list is duplicated, adding 360 degrees to each angle, effectively doubling its size to 2N. Therefore, the auxiliary space used grows linearly with the number of input points, N, resulting in a space complexity of O(N).

Edge Cases

Case	How to Handle
Empty points array	Return 0, as no points can be visible.
All points are at the same location as the location	Count these points separately as they are always visible.
Extremely large input (number of points close to the maximum allowed)	Ensure the solution scales efficiently, potentially using optimized sorting or data structures.
Extremely small angular difference between points	Floating-point precision issues may arise; use an epsilon value for comparisons.
View angle is 0 or 360 degrees	Handle cases where the view angle doesn't allow for any points to be seen, and return appropriate value, likely 0.
Points that form angles that are 0, 90, 180 or 270 degrees relative to location (axis aligned points)	Test all quadrants and boundaries accurately for corner test cases.
Location is extremely far from the points	Calculations might result in zero angles, and we need to handle them correctly and compare them with epsilon value.
Points with identical angles relative to location	Count all points with identical angles within view angle.