Minimum Height Trees

Medium

Google

1 view

Topics:

GraphsTrees

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [a_i, b_i] indicates that there is an undirected edge between the two nodes a_i and b_i in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Constraints:

1 <= n <= 2 * 10⁴
edges.length == n - 1
0 <= a_i, b_i < n
a_i != b_i
All the pairs (a_i, b_i) are distinct.
The given input is guaranteed to be a tree and there will be no repeated edges.

Minimum Height Trees

Medium

Google

1 view

Topics:

GraphsTrees

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [a_i, b_i] indicates that there is an undirected edge between the two nodes a_i and b_i in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

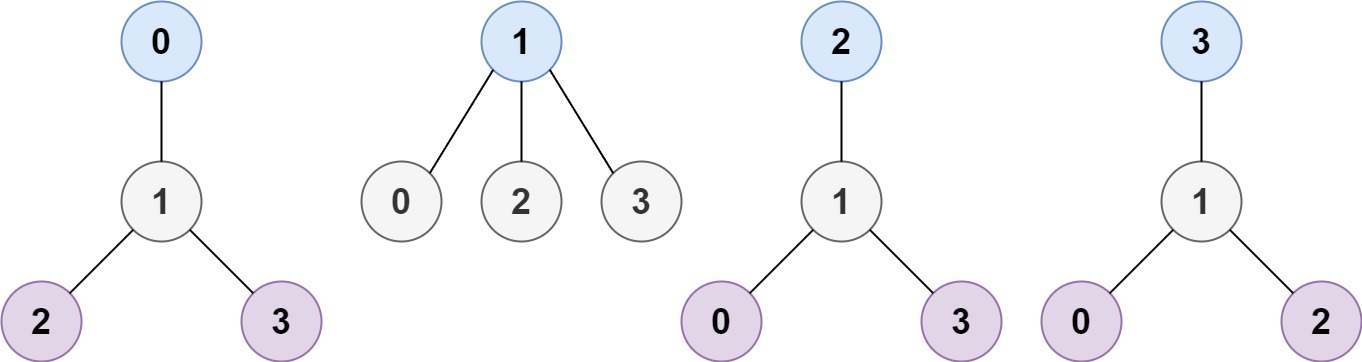
Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

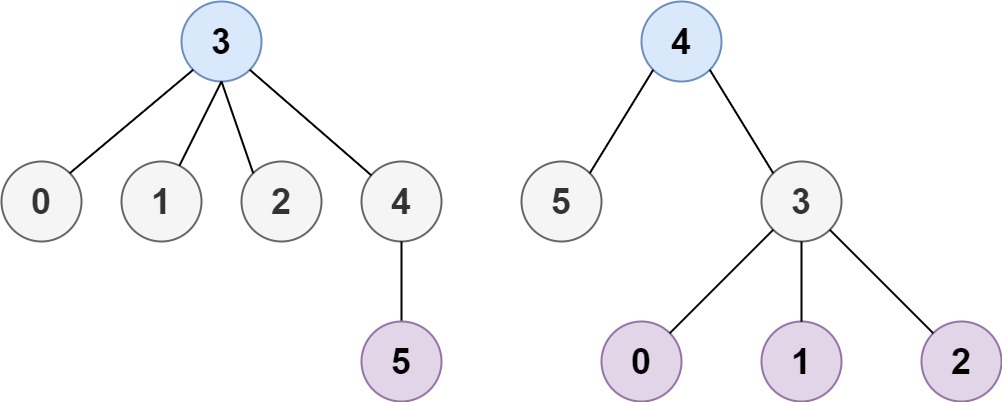
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Constraints:

1 <= n <= 2 * 10⁴
edges.length == n - 1
0 <= a_i, b_i < n
a_i != b_i
All the pairs (a_i, b_i) are distinct.
The given input is guaranteed to be a tree and there will be no repeated edges.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the range of values for 'n', the number of nodes, and what is the maximum number of edges I should expect?
Can the input 'edges' contain duplicate edges, and are the edges directed or undirected?
Is it possible for the input graph to be disconnected, and if so, how should I handle that case?
If there are multiple possible minimum height trees, is the order of the nodes in the returned list important?
If the input graph consists of a single node (n=1 and edges is empty), what should the expected output be?

Brute Force Solution

Approach

The goal is to find the 'center' of a network by trying every possible node as the root. For each potential root, we determine the height of the resulting tree. The brute force approach involves checking every node to see if it produces the smallest possible height.

Here's how the algorithm would work step-by-step:

Pick a node from the network and imagine it as the very top of a tree.
From this 'top' node, figure out how tall the tree would be.
Write down how tall the tree is that you just made.
Now, pick a *different* node and imagine *it* as the very top of the tree.
Again, figure out how tall the tree would be with this new top.
Compare this new height to the height you wrote down earlier. If it's shorter, replace the old height with the new one.
Keep doing this, picking a new node as the top each time, calculating the height, and comparing it to the shortest height you've found so far.
After you've tried every single node as the top, the shortest height you wrote down is the height you're looking for.
Any node that created a tree with that shortest height is one of the 'center' nodes.

Code Implementation

def find_minimum_height_trees_brute_force(number_of_nodes, edges):
    if number_of_nodes <= 0:
        return []
    if number_of_nodes == 1:
        return [0]

    graph = [[] for _ in range(number_of_nodes)]
    for start_node, end_node in edges:
        graph[start_node].append(end_node)
        graph[end_node].append(start_node)

    minimum_height = float('inf')
    minimum_height_trees = []

    for root_node in range(number_of_nodes):
        # Perform a Breadth-First Search to calculate the height of the tree
        queue = [(root_node, 0)]
        visited = {root_node}
        current_height = 0

        while queue:
            node, height = queue.pop(0)
            current_height = max(current_height, height)

            for neighbor in graph[node]:
                if neighbor not in visited:
                    visited.add(neighbor)
                    queue.append((neighbor, height + 1))

        # Check if the current height is the minimum height seen so far.
        if current_height < minimum_height:
            minimum_height = current_height
            minimum_height_trees = [root_node]
        elif current_height == minimum_height:
            minimum_height_trees.append(root_node)

    return minimum_height_trees

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n²) – The algorithm iterates through each of the n nodes in the graph, considering each as a potential root for the tree. For each of these n nodes, it calculates the height of the resulting tree, which involves traversing the graph from that root. In the worst-case scenario (e.g., a skewed tree or a graph approaching a complete graph), calculating the height from a given root might require visiting all other nodes, taking O(n) time. Consequently, the algorithm performs an O(n) height calculation for each of the n nodes, resulting in a total time complexity of O(n * n). Therefore, the overall time complexity is O(n²).

Space Complexity

O(N^2) – The described brute force approach calculates the height of a tree for each node considered as the root. The space complexity primarily arises from the tree height calculation for each node. In the worst-case scenario, where the graph resembles a star graph, calculating the height for each of the N nodes may require storing paths of up to length N, which is effectively traversing a large portion of the graph multiple times. Consequently, across all the N nodes, auxiliary storage to represent these paths or visited nodes can accumulate up to O(N^2) in the worst case if intermediate results are stored during the height calculations for each root.

Optimal Solution

Approach

The most efficient strategy resembles peeling layers from an onion. We iteratively remove the leaves (nodes with only one connection) of the tree until we're left with either one or two center nodes, which will be the roots of our minimum height trees.

Here's how the algorithm would work step-by-step:

First, find all the nodes that are essentially leaves of the tree – those with only one connection.
Then, start removing these leaves. As you remove each leaf, update the connections of the remaining nodes.
Keep removing leaves layer by layer. Each removal brings you closer to the center(s) of the tree.
Continue this process until you are left with only one or two nodes. These remaining nodes are the roots of the minimum height trees.
The key idea is that the center(s) of a tree will always be the last node(s) remaining after repeatedly removing the outer layers.

Code Implementation

def find_minimum_height_trees(number_of_nodes, edges):
    if number_of_nodes <= 0:
        return []
    
    if number_of_nodes == 1:
        return [0]

    adjacency_list = [set() for _ in range(number_of_nodes)]
    for start_node, end_node in edges:
        adjacency_list[start_node].add(end_node)
        adjacency_list[end_node].add(start_node)

    # Identify initial leaves, which have only one connection.
    leaves = [node for node in range(number_of_nodes) if len(adjacency_list[node]) == 1]

    remaining_nodes = number_of_nodes

    # Iteratively remove leaves until we have at most 2 nodes.
    while remaining_nodes > 2:
        remaining_nodes -= len(leaves)
        new_leaves = []

        # Process each leaf and update the adjacency list.
        for leaf in leaves:
            neighbor = adjacency_list[leaf].pop()
            adjacency_list[neighbor].remove(leaf)

            # If a neighbor becomes a leaf, add it to the next layer of leaves.
            if len(adjacency_list[neighbor]) == 1:
                new_leaves.append(neighbor)

        leaves = new_leaves

    # The remaining nodes are the roots of the MHTs.
    return leaves

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n) – The algorithm iterates through all n nodes to find the initial leaves, which takes O(n) time. The while loop runs until only one or two nodes remain. Inside the loop, each node is visited and potentially removed only once. The adjacency list is updated as leaves are removed. The removal operation and updates within the while loop collectively touch each edge a constant number of times. Since the number of edges in a tree is at most n-1, the operations inside the while loop are bounded by O(n). Therefore, the overall time complexity is O(n).

Space Complexity

O(N) – The algorithm utilizes an adjacency list to represent the graph, which stores neighbors for each node, requiring O(N) space where N is the number of nodes (and potentially edges). A queue or list to store the initial leaves also takes O(N) space in the worst-case scenario (e.g., a star graph). The algorithm also implicitly maintains the degree (number of connections) of each node, contributing O(N) space. Thus, the overall auxiliary space complexity is dominated by these O(N) components.

Edge Cases

Case	How to Handle
Empty graph (n=0)	Return an empty list as there are no nodes or trees to compute.
Single node graph (n=1)	Return a list containing only node 0, as it's the only possible root.
Two node graph (n=2)	Return a list containing both node 0 and 1, as either can be the root with minimum height 0.
Disconnected graph	The algorithm will only process the connected component containing node 0, which is incorrect; a check is needed to ensure the entire graph is connected and an error or empty list should be returned if disconnected.
Graph with cycles	The algorithm works correctly with cycles, as the degree-based removal process eventually reduces the graph to its 'center'.
Large graph (n approaching memory limits)	The space complexity of the adjacency list might become an issue; consider alternative representations for extremely large graphs, and ensure appropriate data types are used to prevent integer overflow when calculating degrees.
Star graph (one node connected to all others)	The algorithm correctly identifies the central node as the root of the minimum height tree.
Complete graph (every node connected to every other node)	Any node can serve as the root, and the algorithm should correctly return a list of all nodes.