Uncrossed Lines

Medium

Google

1 view

Topics:

ArraysDynamic Programming

You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.

We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:

nums1[i] == nums2[j], and
the line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).

Return the maximum number of connecting lines we can draw in this way.

Example 1:

Input: nums1 = [1,4,2], nums2 = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from nums1[1] = 4 to nums2[2] = 4 will intersect the line from nums1[2]=2 to nums2[1]=2.

Example 2:

Input: nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
Output: 3

Example 3:

Input: nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
Output: 2

Constraints:

1 <= nums1.length, nums2.length <= 500
1 <= nums1[i], nums2[j] <= 2000

Uncrossed Lines

Medium

Google

1 view

Topics:

ArraysDynamic Programming

You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.

We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:

nums1[i] == nums2[j], and
the line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).

Return the maximum number of connecting lines we can draw in this way.

Example 1:

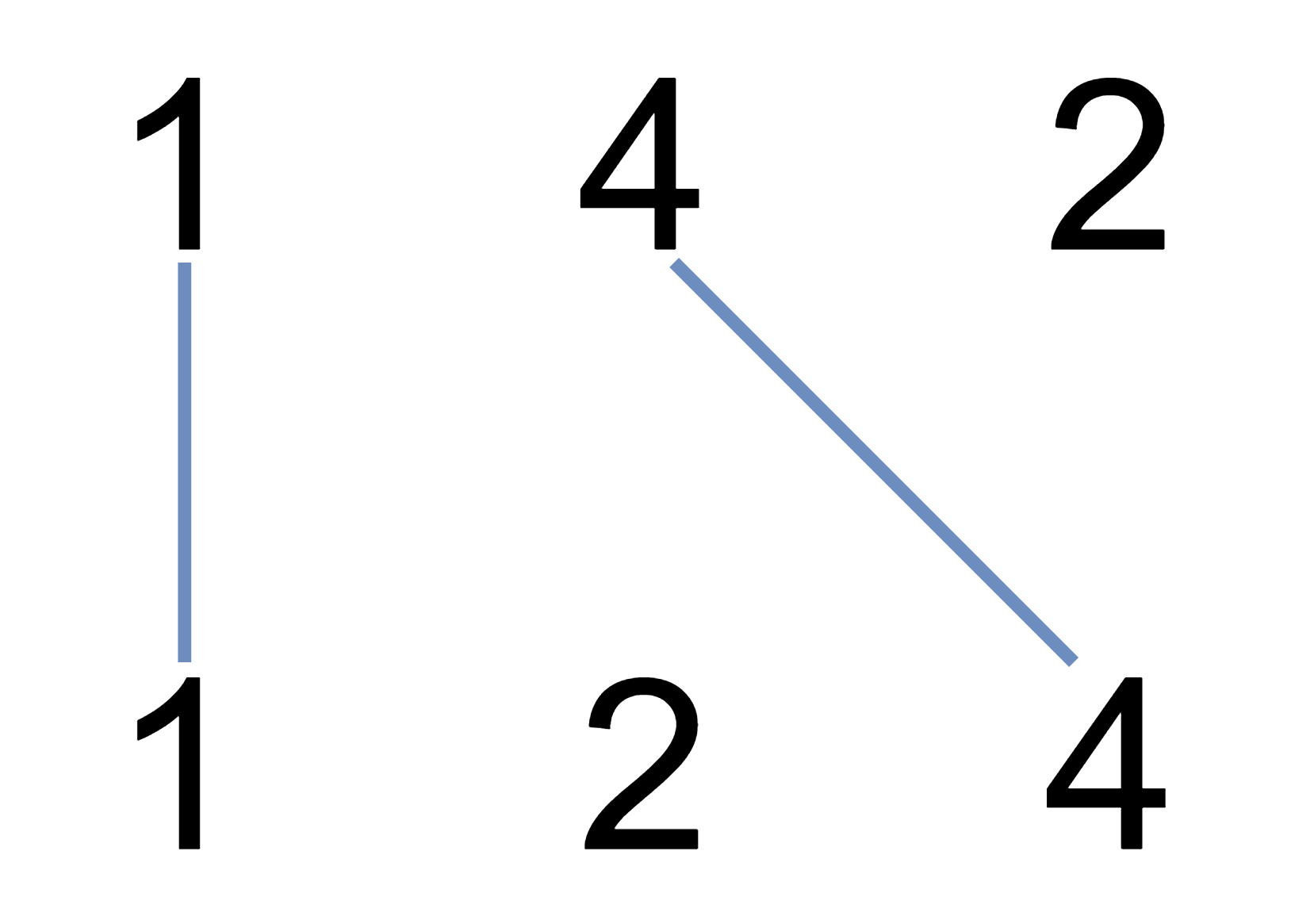
Input: nums1 = [1,4,2], nums2 = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from nums1[1] = 4 to nums2[2] = 4 will intersect the line from nums1[2]=2 to nums2[1]=2.

Example 2:

Input: nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
Output: 3

Example 3:

Input: nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
Output: 2

Constraints:

1 <= nums1.length, nums2.length <= 500
1 <= nums1[i], nums2[j] <= 2000

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the possible ranges for the integer values within the input arrays?
Are duplicates allowed within either of the input arrays, and if so, how should they be handled when determining uncrossed lines?
If no uncrossed lines can be formed, what value should I return?
What are the maximum possible lengths of the input arrays?
Does the relative ordering of the chosen numbers from A and B matter when defining an uncrossed line, or only that the indices are the same?

Brute Force Solution

Approach

The uncrossed lines problem asks us to find the maximum number of lines we can draw between two lists of numbers without any lines crossing. The brute force method involves trying every possible combination of connecting numbers between the two lists and seeing which combination results in the most lines without any crossings.

Here's how the algorithm would work step-by-step:

Consider all possible ways to connect the first number in the first list to a number in the second list.
For each of these connections, explore all possible ways to connect the second number in the first list to a number in the second list, making sure the new line doesn't cross any previously drawn lines.
Continue this process for each number in the first list, always ensuring no lines cross.
Keep track of the number of lines you've drawn for each valid combination of connections (no crossings).
Once you've exhausted all possible combinations of connections, select the combination that resulted in the highest number of lines drawn. That's the answer.

Code Implementation

def uncrossed_lines_brute_force(list_one, list_two):
    def is_crossing(line_one, line_two):
        return line_one[0] < line_two[0] and line_one[1] > line_two[1] or \
               line_one[0] > line_two[0] and line_one[1] < line_two[1]

    def find_max_lines(index_one, current_lines):
        # If we've reached the end of list_one, return the number of lines.
        if index_one == len(list_one):
            return len(current_lines)

        max_lines = len(current_lines)

        for index_two in range(len(list_two)):
            if list_one[index_one] == list_two[index_two]:
                new_line = (index_one, index_two)
                crossing = False
                for existing_line in current_lines:
                    if is_crossing(new_line, existing_line):
                        crossing = True
                        break

                # Only recurse if the new line does not cross existing lines
                if not crossing:

                    # Explore adding the new line and proceeding to the next index.
                    max_lines = max(max_lines, find_max_lines(index_one + 1, current_lines + [new_line]))

        # Also explore the possibility of not drawing a line for the current index.
        max_lines = max(max_lines, find_max_lines(index_one + 1, current_lines))
        return max_lines

    # Start the recursion with the first index and an empty list of lines.
    return find_max_lines(0, [])

Big(O) Analysis

Time Complexity

O(2^(m+n)) – The brute force approach described explores all possible combinations of connections between the two lists, where 'm' is the length of the first list and 'n' is the length of the second list. In the worst case, each element in the first list can potentially connect to any element in the second list, leading to an exponential number of possible combinations. Specifically, each element in the first list has 2^n possibilities (either connect to an element in the second list or not), and this is repeated for all 'm' elements in the first list. Considering also the need to check for crossings which adds to the computational burden, the total number of operations grows exponentially with both m and n. This behavior approximates O(2^(m+n)).

Space Complexity

O(2^N) – The brute force approach explores all possible combinations of connecting numbers between the two lists. Each number in the first list can potentially connect to any number in the second list or not connect at all, leading to an exponential number of possibilities. The number of lines drawn for each valid combination is tracked, which is implicitly stored on the call stack as each recursive call explores a new connection possibility. In the worst case, where N represents the length of the first list, the number of recursive calls, and thus stack frames, grows exponentially, resulting in O(2^N) space complexity due to the implicit storage of call stacks and intermediate line counts for all possible combinations.

Optimal Solution

Approach

The best way to solve this problem is by thinking about matching numbers in the two lists. The goal is to find the longest sequence of matching numbers where the matches appear in the same order in both lists, avoiding crisscrossing lines.

Here's how the algorithm would work step-by-step:

Imagine you're building your sequence of matches gradually. Start by looking at the beginning of both number lists.
For each pair of numbers you look at, you have two choices: either include the pair in your matching sequence, or don't.
You should only include a pair if the numbers are the same. If they're different, you skip it and move on.
When you have multiple options to match, pick the pair that gives you the longest possible matching sequence overall. This means considering all the numbers further down the lists, not just the ones you see right now.
Continue working your way through the lists, always making the choice that leads to the longest matching sequence. This means you might skip some potential matches early on to get to better matches later.
In the end, the number of matches in your longest sequence is the answer.

Code Implementation

def max_uncrossed_lines(number_list_one, number_list_two):
    list_one_length = len(number_list_one)
    list_two_length = len(number_list_two)

    # Initialize a table to store results of subproblems.
    dp_table = [[0] * (list_two_length + 1) for _ in range(list_one_length + 1)]

    for i in range(1, list_one_length + 1):
        for j in range(1, list_two_length + 1):

            # If the numbers match, increment the length of sequence.
            if number_list_one[i - 1] == number_list_two[j - 1]:

                # We found a match, extend previous best subsequence.
                dp_table[i][j] = dp_table[i - 1][j - 1] + 1

            else:

                # No match, take the best of the two adjacent subproblems.
                dp_table[i][j] = max(dp_table[i - 1][j], dp_table[i][j - 1])

    # The bottom-right cell contains the length of longest sequence.
    return dp_table[list_one_length][list_two_length]

Big(O) Analysis

Time Complexity

O(m*n) – The described approach is essentially a dynamic programming solution to find the Longest Common Subsequence (LCS) length between the two input arrays, nums1 and nums2, of sizes m and n, respectively. The algorithm implicitly involves building a table (though not explicitly mentioned in the provided explanation) where each cell dp[i][j] represents the length of the LCS between the first i elements of nums1 and the first j elements of nums2. Computing each cell requires a constant time operation (comparison and potentially taking the maximum of two adjacent cells), and we need to compute m*n such cells. Therefore, the overall time complexity is O(m*n).

Space Complexity

O(N*M) – The described approach implicitly suggests using dynamic programming, where we store intermediate results for subproblems to avoid recomputation. This likely involves creating a table (e.g., a 2D array or matrix) to store the lengths of the longest common subsequences for different prefixes of the input lists. If the input lists have lengths N and M respectively, this table would require N*M space to store the intermediate lengths, leading to O(N*M) auxiliary space, where N and M are the lengths of the two input lists.

Edge Cases

Case	How to Handle
Either input array A or B is null or empty.	Return 0, as no lines can be drawn if one or both arrays are empty.
One array is significantly larger than the other (extreme size difference).	The DP table should be sized according to the input arrays to avoid unnecessary memory usage, ensuring efficient memory utilization.
Arrays A and B have no common elements.	The longest common subsequence will be 0, so the result should be 0.
Arrays A and B are identical.	The result will be the length of either array since every element forms an uncrossed line.
Arrays contain very large numbers that could potentially cause integer overflow during intermediate calculations (although less applicable here).	Use `int` data type, as the problem constraints specify array element values between 1 and 2000, not leading to overflow.
Maximum array lengths (500) are reached, potentially causing time limit exceeded if the algorithm isn't efficient.	The O(m*n) dynamic programming solution should be efficient enough, but verify time complexity to prevent timeouts.
Arrays contain duplicate values with multiple possible uncrossed lines.	The dynamic programming approach implicitly handles this by finding the longest common subsequence, maximizing uncrossed lines.
A and B are the same length but have entirely different elements	Return 0 since there are no common elements and no lines can be drawn.