Decode the Slanted Ciphertext
MediumA string originalText is encoded using a slanted transposition cipher to a string encodedText with the help of a matrix having a fixed number of rows rows.
originalText is placed first in a top-left to bottom-right manner.

The blue cells are filled first, followed by the red cells, then the yellow cells, and so on, until we reach the end of originalText. The arrow indicates the order in which the cells are filled. All empty cells are filled with ' '. The number of columns is chosen such that the rightmost column will not be empty after filling in originalText.
encodedText is then formed by appending all characters of the matrix in a row-wise fashion.
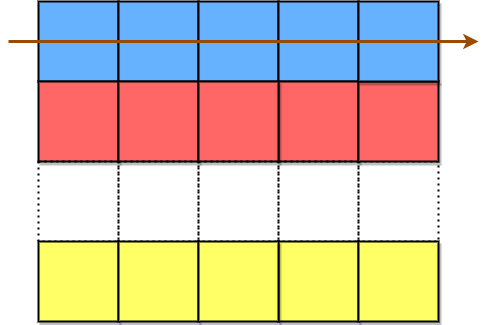
The characters in the blue cells are appended first to encodedText, then the red cells, and so on, and finally the yellow cells. The arrow indicates the order in which the cells are accessed.
For example, if originalText = "cipher" and rows = 3, then we encode it in the following manner:
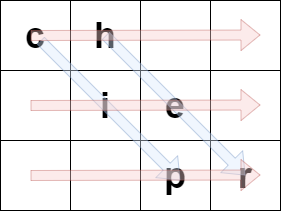
The blue arrows depict how originalText is placed in the matrix, and the red arrows denote the order in which encodedText is formed. In the above example, encodedText = "ch ie pr".
Given the encoded string encodedText and number of rows rows, return the original string originalText.
Note: originalText does not have any trailing spaces ' '. The test cases are generated such that there is only one possible originalText.
Example 1:
Input: encodedText = "ch ie pr", rows = 3 Output: "cipher" Explanation: This is the same example described in the problem description.
Example 2:
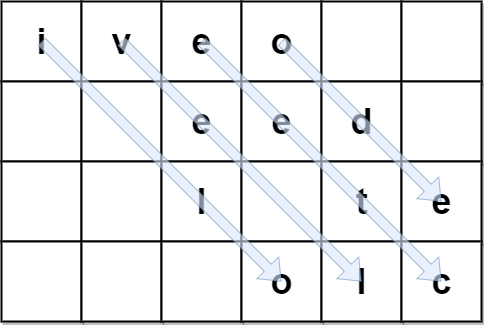
Input: encodedText = "iveo eed l te olc", rows = 4 Output: "i love leetcode" Explanation: The figure above denotes the matrix that was used to encode originalText. The blue arrows show how we can find originalText from encodedText.
Example 3:

Input: encodedText = "coding", rows = 1 Output: "coding" Explanation: Since there is only 1 row, both originalText and encodedText are the same.
Constraints:
0 <= encodedText.length <= 106encodedTextconsists of lowercase English letters and' 'only.encodedTextis a valid encoding of someoriginalTextthat does not have trailing spaces.1 <= rows <= 1000- The testcases are generated such that there is only one possible
originalText.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What characters will the encoded text contain? Will it only be alphanumeric, or could it include special characters or whitespace?
- What is the relationship between the encoded text's length and the number of rows and columns used in the encoding grid? Is there always a valid grid size?
- If the number of rows or columns is not explicitly provided, should I assume a square grid or is there a specific priority (e.g., minimize rows)?
- If the encoded text's length does not perfectly fit a rectangular grid, how should the grid be padded? Should it be padded with a specific character or left partially unfilled?
- What should the function return if the input encoded text is null or empty?
Brute Force Solution
Approach
The brute force method for decoding the slanted ciphertext involves trying every possible configuration for the grid that was used to encrypt the message. This means testing many different dimensions for the grid until the correct one is found, which reveals the original message when read row by row.
Here's how the algorithm would work step-by-step:
- Assume different numbers of columns in the grid, starting from a small number and going larger.
- With each number of columns, calculate how many rows the grid would need to hold the entire coded message.
- Imagine filling the grid diagonally with the coded message based on that column/row combination.
- Read the grid row by row to see if the result makes sense as a possible message. A good message would have meaningful words.
- If the resulting row-by-row read is gibberish, try a different number of columns.
- Continue doing this until you find a column/row combination that gives a legible message when read row by row.
Code Implementation
def decode_the_slanted_ciphertext(encoded_string, grid_columns_max):
string_length = len(encoded_string)
# Iterate through possible number of columns
for grid_columns in range(1, grid_columns_max + 1):
grid_rows = (string_length + grid_columns - 1) // grid_columns
grid = [['' for _ in range(grid_columns)] for _ in range(grid_rows)]
string_index = 0
# Fill the grid diagonally
for column_index in range(grid_columns):
current_row = 0
current_column = column_index
while current_row < grid_rows and current_column < grid_columns and string_index < string_length:
grid[current_row][current_column] = encoded_string[string_index]
string_index += 1
current_row += 1
current_column += 1
# Read the grid row by row to form the decoded text
decoded_text = ''
for row_index in range(grid_rows):
for column_index in range(grid_columns):
decoded_text += grid[row_index][column_index]
#Remove padding from decoded text.
decoded_text = decoded_text.rstrip()
if len(decoded_text) > 0:
return decoded_text
return ""Big(O) Analysis
Optimal Solution
Approach
The key to decoding this special ciphertext is understanding its slanted pattern and how the original text was arranged in a grid. We need to reverse this process by carefully extracting characters from the ciphertext in the correct diagonal order to rebuild the original message.
Here's how the algorithm would work step-by-step:
- Figure out the dimensions (rows and columns) of the grid that the original message was written into. This can be determined from the ciphertext length and the given number of rows.
- Imagine the grid and visualize how the ciphertext was created by reading diagonally. Each diagonal starts from the top row and moves down and to the right (or wraps around).
- Extract the characters by following these diagonals. Start with the first character, then find the next character along the appropriate diagonal path.
- Continue extracting characters along each diagonal until you've covered the entire ciphertext.
- Combine all the extracted characters in the order they were read from the diagonals to form the original, decoded message.
Code Implementation
def decode_ciphertext(encoded_string, number_of_rows):
string_length = len(encoded_string)
number_of_columns = string_length // number_of_rows
decoded_string = ""
# Iterate through each diagonal.
for diagonal_start in range(number_of_columns):
row_index = 0
column_index = diagonal_start
while row_index < number_of_rows and column_index < number_of_columns:
decoded_string += encoded_string[row_index * number_of_columns + column_index]
row_index += 1
column_index += 1
# Process diagonals starting from the second row
for row_start in range(1, number_of_rows):
row_index = row_start
column_index = 0
#Extract characters diagonally
while row_index < number_of_rows and column_index < number_of_columns:
decoded_string += encoded_string[row_index * number_of_columns + column_index]
row_index += 1
column_index += 1
# Reconstruct the original message.
return decoded_stringBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty string ciphertext or rows/cols are zero | Return an empty string immediately as there is nothing to decode. |
| Number of rows is larger than the length of the ciphertext | Return the original ciphertext as no slanted pattern is possible. |
| Ciphertext length is not perfectly divisible by the rows*cols | Pad the ciphertext with a designated character (e.g., space) to make it divisible. |
| Ciphertext contains only spaces | Return the same string of spaces after decoding, maintaining the original length. |
| Rows or columns are equal to 1 | Handle this as a special case where either the string is read directly or transposed depending on which is 1. |
| The given encoded string results in impossible rectangle, row*col != len(encodedText) | Return an empty string or an error if the row * col configuration given is incompatible with the length of the ciphertext. |
| Very large ciphertext, large number of rows and cols (potential memory issues) | Ensure that the memory allocation for the intermediate grid does not exceed available resources. |
| The decoding process is cyclic/repeats itself due to incorrect row/col setup | Detect such cycles during the decoding step and return an error to avoid infinite loops. |