Count Islands With Total Value Divisible by K
MediumYou are given an m x n matrix grid and a positive integer k. An island is a group of positive integers (representing land) that are 4-directionally connected (horizontally or vertically).
The total value of an island is the sum of the values of all cells in the island.
Return the number of islands with a total value divisible by k.
Example 1:
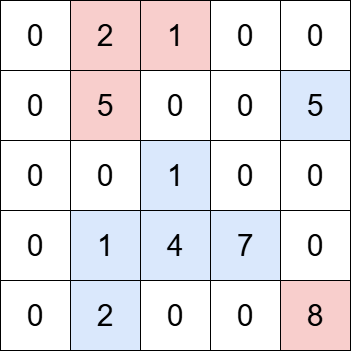
Input: grid = [[0,2,1,0,0],[0,5,0,0,5],[0,0,1,0,0],[0,1,4,7,0],[0,2,0,0,8]], k = 5
Output: 2
Explanation:
The grid contains four islands. The islands highlighted in blue have a total value that is divisible by 5, while the islands highlighted in red do not.
Example 2:
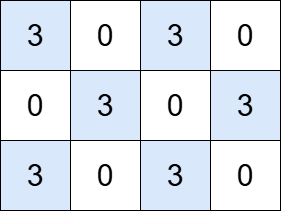
Input: grid = [[3,0,3,0], [0,3,0,3], [3,0,3,0]], k = 3
Output: 6
Explanation:
The grid contains six islands, each with a total value that is divisible by 3.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 1050 <= grid[i][j] <= 1061 <= k <= 106
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the grid (max rows and cols), and what is the maximum possible value for a cell in the grid, and the value of 'k'?
- Can the grid be empty (0 rows or 0 columns)? If so, what should I return?
- Is a cell with a value of 0 considered part of any island, or does it always act as a separator between islands?
- What defines 'connected'? Are we only considering horizontally and vertically adjacent cells, or also diagonally adjacent cells?
- If multiple islands have a sum divisible by k, should I count each of them, or is there a case where certain islands should be treated as duplicates?
Brute Force Solution
Approach
The brute force approach systematically explores all possible island combinations within the given grid. For each combination, we calculate the total value and check if it's divisible by K. By trying every single possibility, we guarantee that we will find and count all valid islands.
Here's how the algorithm would work step-by-step:
- Consider every single cell in the grid as the potential starting point of an island.
- For each starting cell, explore all connected cells (up, down, left, right) to form different island shapes and sizes.
- Calculate the sum of the values of all the cells in the current island.
- Check if the total value of the island is evenly divisible by K (meaning there's no remainder when dividing by K).
- If the total value is divisible by K, increment a counter to keep track of the number of valid islands.
- Repeat this process for every possible island combination that can be formed from each starting cell.
- Finally, after exploring all possibilities, return the total count of islands whose sum is divisible by K.
Code Implementation
def count_islands_divisible_by_k_brute_force(grid, k):
rows = len(grid)
cols = len(grid[0])
visited = set()
island_count = 0
def explore_island(row, col, current_island_nodes, current_island_sum):
if (row < 0 or row >= rows or col < 0 or col >= cols or\
(row, col) in visited or grid[row][col] == 0):
return current_island_sum
visited.add((row, col))
current_island_sum += grid[row][col]
current_island_nodes.append((row, col))
# Explore neighbors
current_island_sum = explore_island(row + 1, col, current_island_nodes, current_island_sum)
current_island_sum = explore_island(row - 1, col, current_island_nodes, current_island_sum)
current_island_sum = explore_island(row, col + 1, current_island_nodes, current_island_sum)
current_island_sum = explore_island(row, col - 1, current_island_nodes, current_island_sum)
return current_island_sum
for row_index in range(rows):
for col_index in range(cols):
if grid[row_index][col_index] != 0 and (row_index, col_index) not in visited:
#Start exploring from each unvisited land cell.
current_island_nodes = []
island_sum = explore_island(row_index, col_index, current_island_nodes, 0)
# Check if island sum is divisible by k.
if island_sum % k == 0:
island_count += 1
return island_countBig(O) Analysis
Optimal Solution
Approach
The problem involves finding separate land masses on a map and checking if the total value of each land mass is divisible by a given number. The best way to do this is to explore each land mass piece by piece, adding up their values and marking them as visited to avoid counting them again.
Here's how the algorithm would work step-by-step:
- Go through each square on the map, one by one.
- If a square is land and hasn't been visited yet, start exploring it.
- As you explore a land mass, keep a running total of the value of each square you find and mark each explored square as visited.
- To explore a land mass, look at the squares next to the current one (up, down, left, and right). If they are land and haven't been visited, add them to the land mass and continue exploring from there.
- Once you've explored the entire land mass, check if the total value you calculated is divisible by the given number.
- If the total value is divisible by the number, increase the counter.
- Continue scanning the map, exploring new land masses and checking their total values until you've checked every square.
- The final count represents the number of land masses with a total value divisible by the number.
Code Implementation
def count_islands_divisible_by_k(grid, k):
rows = len(grid)
cols = len(grid[0])
visited = [[False] * cols for _ in range(rows)]
island_count = 0
def depth_first_search(row, col):
if row < 0 or row >= rows or col < 0 or col >= cols or visited[row][col] or grid[row][col] == 0:
return 0
visited[row][col] = True
island_value = grid[row][col]
# Recursively explore neighboring land cells.
island_value += depth_first_search(row + 1, col)
island_value += depth_first_search(row - 1, col)
island_value += depth_first_search(row, col + 1)
island_value += depth_first_search(row, col - 1)
return island_value
for row in range(rows):
for col in range(cols):
# Start DFS if it's land and not visited.
if grid[row][col] != 0 and not visited[row][col]:
total_island_value = depth_first_search(row, col)
# Check if the sum is divisible by k.
if total_island_value % k == 0:
island_count += 1
return island_countBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty grid | Return 0 immediately as there are no islands. |
| Grid with all zero values | Return 0 as no cells have values greater than 0 and hence no islands exist. |
| Grid with only one cell having a value divisible by K | The single cell forms an island, and if its value is divisible by K, the result is 1. |
| Grid with a single island whose sum is not divisible by K | The algorithm should correctly identify and return 0. |
| Large grid where recursion depth might exceed the stack limit | Use an iterative approach (e.g., BFS or DFS with a stack) to avoid stack overflow. |
| Integer overflow when calculating island sum | Use a larger data type (e.g., long) to store the island sum, or use modular arithmetic during sum calculation. |
| K is zero | Handle division by zero by returning 0 if K is 0. |
| Grid contains only one large island that spans nearly the entire grid | Algorithm should efficiently traverse the entire island without errors or performance degradation. |