Max Area of Island
MediumYou are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The area of an island is the number of cells with a value 1 in the island.
Return the maximum area of an island in grid. If there is no island, return 0.
Example 1:
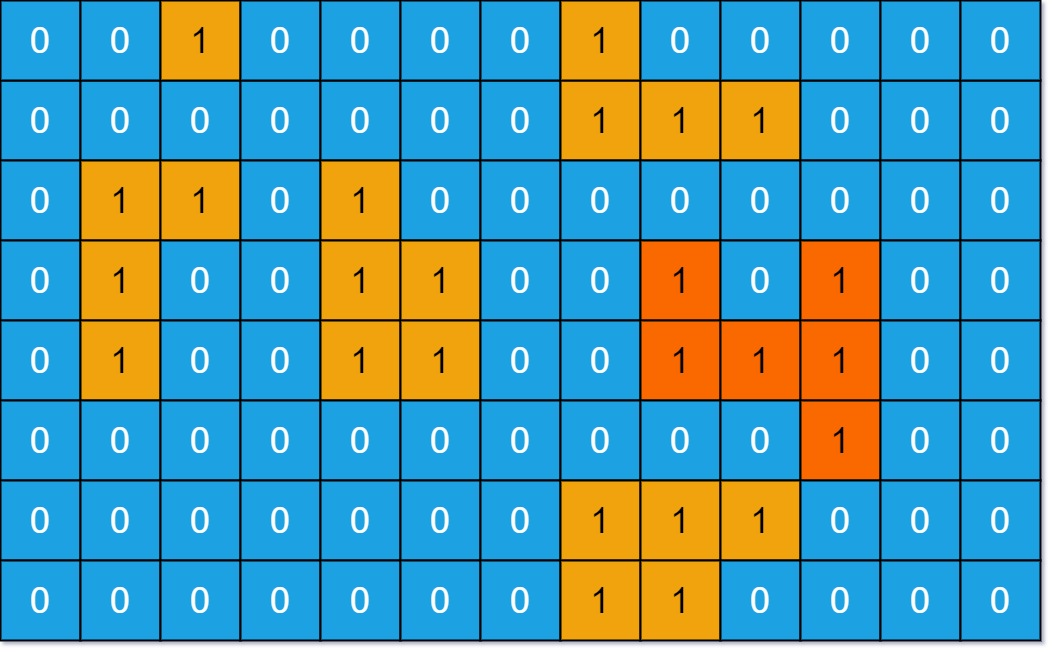
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] Output: 6 Explanation: The answer is not 11, because the island must be connected 4-directionally.
Example 2:
Input: grid = [[0,0,0,0,0,0,0,0]] Output: 0
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 50grid[i][j]is either0or1.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the grid, and what is the maximum size I should expect for each dimension?
- Is the grid guaranteed to be rectangular, or can it be irregularly shaped?
- What should I return if the grid is empty or if there are no islands (all values are 0)?
- Are the grid values guaranteed to be only 0 or 1, or could there be other integer values?
- By 'connected', do you mean 4-directionally (up, down, left, right) or 8-directionally connected?
Brute Force Solution
Approach
Imagine you are looking at a map with islands represented as land and water. The brute force approach involves meticulously exploring every piece of land to determine the size of each island. We will visit each landmass and count how big it is to determine which island is the largest.
Here's how the algorithm would work step-by-step:
- Start by looking at the first square on the map.
- If it's land, explore the entire connected island starting from that square by checking all adjacent land squares.
- Count the number of land squares connected to that original square.
- Once you have found the size of the first island, mark all of its squares as visited so that you don't count it again.
- Move on to the next unvisited square on the map.
- If it's land and hasn't been visited, repeat the island exploring process as done earlier, counting the squares and marking them as visited.
- Keep track of the size of each island you find.
- Once you have explored the entire map, compare the sizes of all the islands you found.
- The largest size that you find is the answer.
Code Implementation
def max_area_of_island_brute_force(grid):
if not grid:
return 0
number_of_rows = len(grid)
number_of_columns = len(grid[0])
visited = [[False] * number_of_columns for _ in range(number_of_rows)]
max_island_area = 0
def explore_island(row, column):
if row < 0 or row >= number_of_rows or column < 0 or column >= number_of_columns or \
visited[row][column] or grid[row][column] == 0:
return 0
# Mark the current cell as visited to avoid re-counting
visited[row][column] = True
area = 1
area += explore_island(row + 1, column)
area += explore_island(row - 1, column)
area += explore_island(row, column + 1)
area += explore_island(row, column - 1)
return area
for row in range(number_of_rows):
for column in range(number_of_columns):
# Only explore if it's land and unvisited
if grid[row][column] == 1 and not visited[row][column]:
island_area = explore_island(row, column)
# Update the maximum island size seen so far
max_island_area = max(max_island_area, island_area)
return max_island_areaBig(O) Analysis
Optimal Solution
Approach
Imagine the land is a map of islands in the sea. We want to find the biggest island. The best way to do this is to explore each island completely as we find it and keep track of which one was the largest.
Here's how the algorithm would work step-by-step:
- Start by scanning the entire map to find a piece of land (part of an island).
- When you find a piece of land, start exploring the entire island it belongs to. To do this, explore all the neighboring land pieces that are connected to the current piece.
- As you explore an island, mark each piece of land as visited so you don't count it again later. This is important to avoid endlessly going back and forth.
- While exploring, keep a running count of how many pieces of land are in the current island. This gives you the size of the island.
- Once you have fully explored an island (meaning you've visited all connected land pieces), compare its size to the size of the biggest island you've seen so far, and update the 'biggest island' size if the current island is larger.
- Continue scanning the map for unexplored pieces of land, repeating the process of exploring and counting islands until the entire map has been scanned.
- The final 'biggest island' size is the answer.
Code Implementation
def max_area_of_island(grid):
if not grid:
return 0
number_of_rows = len(grid)
number_of_columns = len(grid[0])
max_island_area = 0
def explore_island(row, column):
if row < 0 or row >= number_of_rows or \
column < 0 or column >= number_of_columns or \
grid[row][column] == 0:
return 0
# Mark the current cell as visited
grid[row][column] = 0
island_area = 1
# Recursively explore adjacent land
island_area += explore_island(row + 1, column)
island_area += explore_island(row - 1, column)
island_area += explore_island(row, column + 1)
island_area += explore_island(row, column - 1)
return island_area
for row in range(number_of_rows):
for column in range(number_of_columns):
if grid[row][column] == 1:
# Found land, explore the island
current_island_area = explore_island(row, column)
# Update the maximum island area
max_island_area = max(max_island_area, current_island_area)
return max_island_area
def maxAreaOfIsland(grid):
rows = len(grid)
cols = len(grid[0])
max_area = 0
def dfs(row, col):
if row < 0 or row >= rows or col < 0 or col >= cols or grid[row][col] == 0:
return 0
# Mark cell as visited
grid[row][col] = 0
area = 1
# Explore neighbors
area += dfs(row + 1, col)
area += dfs(row - 1, col)
area += dfs(row, col + 1)
area += dfs(row, col - 1)
return area
for row in range(rows):
for col in range(cols):
if grid[row][col] == 1:
# Found an island, explore it
area = dfs(row, col)
# Update max area if needed
max_area = max(max_area, area)
return max_area
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty grid input | Return 0 immediately as there can be no island if the grid is invalid. |
| Grid with 0 rows or 0 columns | Return 0 immediately because an island cannot exist in a grid of size zero. |
| Grid with only one cell that is 0 | Return 0 as the single cell is water, not land. |
| Grid with only one cell that is 1 | Return 1 as the single cell is land representing an island of size 1. |
| Grid filled entirely with 0s | Return 0 as there is no land present. |
| Grid filled entirely with 1s | Return the total number of cells in the grid as the entire grid is one large island. |
| Large grid to test stack overflow with recursive DFS | Implement iterative DFS with a stack to avoid stack overflow errors for large grids, or ensure the chosen language and environment can handle potentially deep recursion if recursive DFS is employed. |
| Grid with multiple disconnected islands of varying sizes | The algorithm should correctly identify and calculate the size of each island, then return the maximum size. |