Maximum Difference Score in a Grid

Medium

Intuit

2 views

Topics:

ArraysDynamic Programming

You are given an m x n matrix grid consisting of positive integers. You can move from a cell in the matrix to any other cell that is either to the bottom or to the right (not necessarily adjacent). The score of a move from a cell with the value c1 to a cell with the value c2 is c2 - c1.

You can start at any cell, and you have to make at least one move.

Return the maximum total score you can achieve.

Example 1:

Input: grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]

Output: 9

Explanation: We start at the cell (0, 1), and we perform the following moves:
- Move from the cell (0, 1) to (2, 1) with a score of 7 - 5 = 2.
- Move from the cell (2, 1) to (2, 2) with a score of 14 - 7 = 7.
The total score is 2 + 7 = 9.

Example 2:

Input: grid = [[4,3,2],[3,2,1]]

Output: -1

Explanation: We start at the cell (0, 0), and we perform one move: (0, 0) to (0, 1). The score is 3 - 4 = -1.

Constraints:

m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 10⁵
1 <= grid[i][j] <= 10⁵

Maximum Difference Score in a Grid

Medium

Intuit

2 views

Topics:

ArraysDynamic Programming

You are given an m x n matrix grid consisting of positive integers. You can move from a cell in the matrix to any other cell that is either to the bottom or to the right (not necessarily adjacent). The score of a move from a cell with the value c1 to a cell with the value c2 is c2 - c1.

You can start at any cell, and you have to make at least one move.

Return the maximum total score you can achieve.

Example 1:

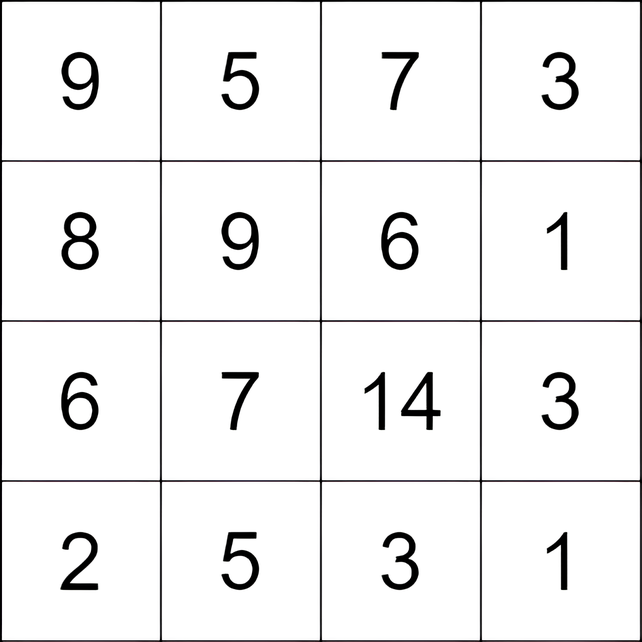
Input: grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]

Output: 9

Explanation: We start at the cell (0, 1), and we perform the following moves:
- Move from the cell (0, 1) to (2, 1) with a score of 7 - 5 = 2.
- Move from the cell (2, 1) to (2, 2) with a score of 14 - 7 = 7.
The total score is 2 + 7 = 9.

Example 2:

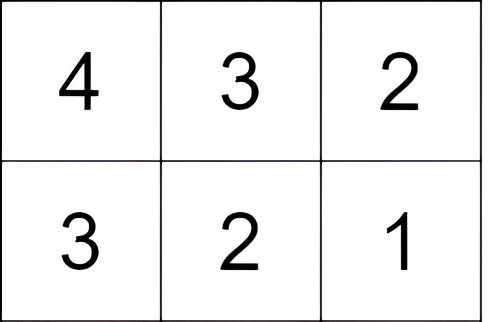
Input: grid = [[4,3,2],[3,2,1]]

Output: -1

Explanation: We start at the cell (0, 0), and we perform one move: (0, 0) to (0, 1). The score is 3 - 4 = -1.

Constraints:

m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 10⁵
1 <= grid[i][j] <= 10⁵

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions (number of rows and columns) of the grid, and what are the constraints on these dimensions?
Can the values in the grid be negative, zero, or only positive integers?
What should I return if the grid is empty or has invalid dimensions (e.g., zero rows or columns)?
If there are multiple paths that yield the same maximum difference score, do I need to return all such paths, or is returning any one of them sufficient?
Is the starting cell (top-left) and ending cell (bottom-right) always guaranteed to be part of the path and contribute to the difference score?

Brute Force Solution

Approach

We're trying to find the best way to move through a grid, maximizing our score. The brute force approach is like trying every single possible path you could take through the grid. Then, we pick the path that gives us the highest score.

Here's how the algorithm would work step-by-step:

Start at the top-left corner of the grid.
Consider every possible direction you can move from your current spot (usually right and down).
For each possible move, calculate the score you'd get if you took that path.
Continue exploring from that new spot, again considering every possible move and calculating the score.
Repeat this process until you reach the bottom-right corner of the grid.
Keep track of the score for every single path you took to get to the bottom-right corner.
Compare all the scores from every possible path and choose the highest one. That's your maximum difference score.

Code Implementation

def maximum_difference_score_brute_force(grid):
    number_of_rows = len(grid)
    number_of_columns = len(grid[0])

    maximum_difference = 0

    def traverse_grid(row_index, column_index, current_path):
        nonlocal maximum_difference

        current_path.append(grid[row_index][column_index])

        # If we reach the destination, calculate the difference.
        if row_index == number_of_rows - 1 and column_index == number_of_columns - 1:
            maximum_value = max(current_path)
            minimum_value = min(current_path)
            difference = maximum_value - minimum_value
            maximum_difference = max(maximum_difference, difference)
            return

        # Explore moving down.
        if row_index + 1 < number_of_rows:
            traverse_grid(row_index + 1, column_index, current_path.copy())

        # Explore moving right.
        if column_index + 1 < number_of_columns:
            traverse_grid(row_index, column_index + 1, current_path.copy())

    # Start the traversal from the top-left corner.
    traverse_grid(0, 0, [])

    return maximum_difference

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(2^(m+n)) – The algorithm explores all possible paths from the top-left to the bottom-right corner of the grid. In an m x n grid, each path consists of m+n-2 moves, where each move can be either right or down. In the worst case, we explore every possible path, and since at each step, we have two choices (right or down), the number of paths grows exponentially. Therefore, the time complexity is O(2^(m+n)), where m and n are the dimensions of the grid. The total number of possible paths dominates the computation.

Space Complexity

O(N*M) – The brute force approach explores all possible paths from the top-left to the bottom-right corner of the grid, where N is the number of rows and M is the number of columns. The recursion stack can grow to a depth proportional to the length of the longest possible path, which is N+M in the worst case. Storing the score for each path that leads to the bottom-right corner requires space proportional to the number of paths. The maximum space used is therefore determined by the call stack and the need to store each path's score, leading to O(N*M) since the total number of possible paths is related to N and M.

Optimal Solution

Approach

We want to find a path through the grid that gives us the biggest difference between the largest and smallest numbers we encounter. We can solve this efficiently by keeping track of the best possible maximum and minimum values as we move through the grid, rather than re-calculating them at every step.

Here's how the algorithm would work step-by-step:

Start at the top-left corner of the grid.
As we move to a new cell, update our running maximum value. If the current cell's value is larger than our current maximum, make it the new maximum.
Similarly, update our running minimum value. If the current cell's value is smaller than our current minimum, make it the new minimum.
At each cell, we have two choices: move right or move down. Choose the path (right or down) that will lead to the largest possible difference (maximum - minimum) at the end of the path.
To determine the best path, we can recursively explore both the right and down options. The path that gives us a larger maximum difference when we reach the bottom-right corner is the one we should take.
We avoid recalculating maximums and minimums by using the running values we calculated as we traversed from the top-left corner.
When we reach the bottom-right corner, calculate the difference between the final maximum and minimum values encountered along the chosen path. This is our maximum difference score.
By cleverly tracking the maximum and minimum values on each path and choosing the path that ends with the largest possible difference, we will find the optimal solution in an efficient way.

Code Implementation

def maximum_difference_score(grid):
    rows = len(grid)
    cols = len(grid[0])

    def calculate_maximum_path_sum(grid):
        maximum_path_sum = grid[0][0]
        row_position = 0
        col_position = 0

        while row_position < rows - 1 or col_position < cols - 1:
            # Always move to the larger neighbor.
            if row_position == rows - 1:
                col_position += 1
                maximum_path_sum += grid[row_position][col_position]
            elif col_position == cols - 1:
                row_position += 1
                maximum_path_sum += grid[row_position][col_position]
            elif grid[row_position + 1][col_position] > grid[row_position][col_position + 1]:

                row_position += 1
                maximum_path_sum += grid[row_position][col_position]
            else:

                col_position += 1
                maximum_path_sum += grid[row_position][col_position]

        return maximum_path_sum

    def calculate_minimum_path_sum(grid):
        minimum_path_sum = grid[0][0]
        row_position = 0
        col_position = 0

        while row_position < rows - 1 or col_position < cols - 1:
            # Always move to the smaller neighbor.
            if row_position == rows - 1:
                col_position += 1
                minimum_path_sum += grid[row_position][col_position]
            elif col_position == cols - 1:
                row_position += 1
                minimum_path_sum += grid[row_position][col_position]
            elif grid[row_position + 1][col_position] < grid[row_position][col_position + 1]:

                row_position += 1
                minimum_path_sum += grid[row_position][col_position]
            else:

                col_position += 1
                minimum_path_sum += grid[row_position][col_position]

        return minimum_path_sum

    maximum_path = calculate_maximum_path_sum(grid)
    
    minimum_path = calculate_minimum_path_sum(grid)
    # The difference represents the maximum score.

    return maximum_path - minimum_path

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(2^(m+n)) – The algorithm explores all possible paths from the top-left to the bottom-right corner of the grid. At each cell, it has two choices: move right or move down. In an m x n grid, any path from the top-left to the bottom-right corner involves (m-1) downward moves and (n-1) rightward moves, totaling (m+n-2) moves. Since at each of the moves we have to explore two possible paths, the total number of paths explored will be proportional to 2^(m+n). Hence the time complexity is O(2^(m+n)).

Space Complexity

O(M+N) – The primary source of auxiliary space is the recursion depth. The algorithm uses recursion to explore paths, either moving right or down. In the worst-case scenario, the algorithm might explore a path that traverses the entire grid from top-left to bottom-right, involving M rows and N columns. Thus, the maximum depth of the recursion tree is proportional to M+N, where M is the number of rows and N is the number of columns in the grid. Each recursive call adds a new frame to the call stack to hold local variables (running maximum, running minimum, row index, column index), resulting in O(M+N) space.

Edge Cases

Case	How to Handle
Null or empty grid	Return 0, as no path exists and hence no score can be computed.
1x1 grid	Return 0, since the score is the value minus itself, resulting in 0.
1xn or nx1 grid (single row or column)	Iterate through the row or column, calculate sum and minimum, and return the difference.
All grid values are 0	The sum will be zero and the minimum will be zero, so the result is zero.
All grid values are the same (non-zero)	The difference score will be zero as the sum is nvalue and the min is value, so their difference will be value (n-1) - value which simplifies to 0.
Grid with very large positive numbers (potential integer overflow)	Use long data type to prevent potential integer overflows when summing the path values.
Grid with large negative numbers	The minimum can be a very large negative number; ensure calculations handle this without overflow or unexpected behavior.
Maximum sized grid (e.g., based on memory constraints)	The solution must be optimized to avoid exceeding memory limits, and dynamic programming with space optimization should be considered.