Most Profitable Path in a Tree

Medium

Intuit

2 views

Topics:

TreesGraphsRecursion

There is an undirected tree with n nodes labeled from 0 to n - 1, rooted at node 0. You are given a 2D integer array edges of length n - 1 where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.

At every node i, there is a gate. You are also given an array of even integers amount, where amount[i] represents:

the price needed to open the gate at node i, if amount[i] is negative, or,
the cash reward obtained on opening the gate at node i, otherwise.

The game goes on as follows:

Initially, Alice is at node 0 and Bob is at node bob.
At every second, Alice and Bob each move to an adjacent node. Alice moves towards some leaf node, while Bob moves towards node 0.
For every node along their path, Alice and Bob either spend money to open the gate at that node, or accept the reward. Note that:
- If the gate is already open, no price will be required, nor will there be any cash reward.
- If Alice and Bob reach the node simultaneously, they share the price/reward for opening the gate there. In other words, if the price to open the gate is c, then both Alice and Bob pay c / 2 each. Similarly, if the reward at the gate is c, both of them receive c / 2 each.
If Alice reaches a leaf node, she stops moving. Similarly, if Bob reaches node 0, he stops moving. Note that these events are independent of each other.

Return the maximum net income Alice can have if she travels towards the optimal leaf node.

Example 1:

Input: edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
Output: 6
Explanation: 
The above diagram represents the given tree. The game goes as follows:
- Alice is initially on node 0, Bob on node 3. They open the gates of their respective nodes.
  Alice's net income is now -2.
- Both Alice and Bob move to node 1. 
  Since they reach here simultaneously, they open the gate together and share the reward.
  Alice's net income becomes -2 + (4 / 2) = 0.
- Alice moves on to node 3. Since Bob already opened its gate, Alice's income remains unchanged.
  Bob moves on to node 0, and stops moving.
- Alice moves on to node 4 and opens the gate there. Her net income becomes 0 + 6 = 6.
Now, neither Alice nor Bob can make any further moves, and the game ends.
It is not possible for Alice to get a higher net income.

Example 2:

Input: edges = [[0,1]], bob = 1, amount = [-7280,2350]
Output: -7280
Explanation: 
Alice follows the path 0->1 whereas Bob follows the path 1->0.
Thus, Alice opens the gate at node 0 only. Hence, her net income is -7280.

Constraints:

2 <= n <= 10⁵
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
edges represents a valid tree.
1 <= bob < n
amount.length == n
amount[i] is an even integer in the range [-10⁴, 10⁴].

Most Profitable Path in a Tree

Medium

Intuit

2 views

Topics:

TreesGraphsRecursion

There is an undirected tree with n nodes labeled from 0 to n - 1, rooted at node 0. You are given a 2D integer array edges of length n - 1 where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.

At every node i, there is a gate. You are also given an array of even integers amount, where amount[i] represents:

the price needed to open the gate at node i, if amount[i] is negative, or,
the cash reward obtained on opening the gate at node i, otherwise.

The game goes on as follows:

Initially, Alice is at node 0 and Bob is at node bob.
At every second, Alice and Bob each move to an adjacent node. Alice moves towards some leaf node, while Bob moves towards node 0.
For every node along their path, Alice and Bob either spend money to open the gate at that node, or accept the reward. Note that:
- If the gate is already open, no price will be required, nor will there be any cash reward.
- If Alice and Bob reach the node simultaneously, they share the price/reward for opening the gate there. In other words, if the price to open the gate is c, then both Alice and Bob pay c / 2 each. Similarly, if the reward at the gate is c, both of them receive c / 2 each.
If Alice reaches a leaf node, she stops moving. Similarly, if Bob reaches node 0, he stops moving. Note that these events are independent of each other.

Return the maximum net income Alice can have if she travels towards the optimal leaf node.

Example 1:

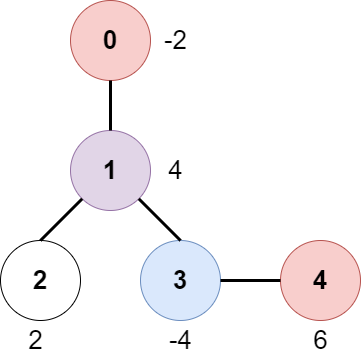
Input: edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
Output: 6
Explanation: 
The above diagram represents the given tree. The game goes as follows:
- Alice is initially on node 0, Bob on node 3. They open the gates of their respective nodes.
  Alice's net income is now -2.
- Both Alice and Bob move to node 1. 
  Since they reach here simultaneously, they open the gate together and share the reward.
  Alice's net income becomes -2 + (4 / 2) = 0.
- Alice moves on to node 3. Since Bob already opened its gate, Alice's income remains unchanged.
  Bob moves on to node 0, and stops moving.
- Alice moves on to node 4 and opens the gate there. Her net income becomes 0 + 6 = 6.
Now, neither Alice nor Bob can make any further moves, and the game ends.
It is not possible for Alice to get a higher net income.

Example 2:

Input: edges = [[0,1]], bob = 1, amount = [-7280,2350]
Output: -7280
Explanation: 
Alice follows the path 0->1 whereas Bob follows the path 1->0.
Thus, Alice opens the gate at node 0 only. Hence, her net income is -7280.

Constraints:

2 <= n <= 10⁵
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
edges represents a valid tree.
1 <= bob < n
amount.length == n
amount[i] is an even integer in the range [-10⁴, 10⁴].

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the possible values for the number of nodes (n) in the tree? Are there any constraints on the range?
Can the `amount` array contain negative values, zero, or only positive values?
The problem states a path from node 0 to a leaf node. Is the tree guaranteed to be connected and have at least one leaf node reachable from node 0?
If there are multiple equally profitable paths, should I return the profit from any one of them, or is there a specific path I should prioritize (e.g., the shortest path)?
The edges are given as a list. Can I assume the input represents a valid tree (connected, no cycles, no self-loops), or do I need to validate the tree structure?

Brute Force Solution

Approach

The brute force approach to finding the most profitable path in a tree involves checking every single possible path from the start to the end. We explore all avenues, calculating the profit for each one. Then, we simply choose the path that yields the highest profit.

Here's how the algorithm would work step-by-step:

Start at the beginning node of the tree.
Consider all possible paths that branch out from this node.
For each of these paths, continue to explore all further possible branches.
Keep going until you reach a leaf node (the end of a path).
Calculate the total profit for that particular path by adding up the values of all the nodes along it.
Repeat steps 2 through 5 for every single possible path from the start to a leaf node.
Compare the total profit of all the paths you've explored.
Select the path with the highest total profit as the most profitable path.

Code Implementation

def most_profitable_path_brute_force(parent_list, profit_list):
    number_of_nodes = len(profit_list)
    graph = [[] for _ in range(number_of_nodes)]

    # Build the tree structure based on parent-child relationships
    for node_index, parent_index in enumerate(parent_list):
        if node_index != 0:
            graph[node_index].append(parent_index)
            graph[parent_index].append(node_index)

    maximum_profit = float('-inf')

    def depth_first_search(current_node, current_path, current_profit):
        nonlocal maximum_profit

        current_path.append(current_node)
        current_profit += profit_list[current_node]

        # Check if it's a leaf node (end of the path)
        if len(graph[current_node]) == 1 and current_node != 0:
            # Calculate the profit of the path
            maximum_profit = max(maximum_profit, current_profit)
            return

        # Explore neighbors, excluding the parent to avoid cycles
        for neighbor in graph[current_node]:
            if neighbor not in current_path:
                # Recursively call DFS for the neighbor
                depth_first_search(neighbor, current_path.copy(), current_profit)

    # Initiate DFS starting from node 0
    depth_first_search(0, [], 0)

    return maximum_profit

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n!) – The brute force approach explores all possible paths in the tree. In the worst-case scenario, the tree could resemble a complete graph. Traversing all possible paths from the root to every leaf involves considering every possible combination of nodes. This leads to exploring all permutations of nodes which gives us a factorial relationship with the number of nodes, n. Therefore, the time complexity is O(n!).

Space Complexity

O(N) – The brute force approach explores all possible paths in the tree using recursion. In the worst-case scenario, the recursion depth can be equal to the height of the tree, which can be N (the number of nodes) in a skewed tree. Each recursive call adds a new frame to the call stack to store the current node and path information, leading to a maximum auxiliary space usage proportional to the tree's height (N). Therefore, the space complexity is O(N) due to the recursion stack.

Optimal Solution

Approach

The problem asks us to find the path in a tree that gives the highest profit. We will find the shortest distances for two people, Alice and Bob, from specific locations to all nodes and then find the most profitable path that takes into account these distances.

Here's how the algorithm would work step-by-step:

First, find the shortest path from Alice's starting location to every other place in the tree. Think of it like drawing the shortest routes from Alice's home to every city.
Next, do the same thing for Bob, finding the shortest route from his starting location to every other place in the tree.
Now, look at each place in the tree and consider how far Alice and Bob have to travel to get there.
If Alice arrives before Bob, she gets all the money from that place. If Bob arrives first, he gets nothing.
If they arrive at the same time, the money is split in half (rounded down to the nearest whole number).
Find the path from the very beginning of the tree that collects the most money following the tree branches.
Keep track of the best possible path and the total profit along the way.
Return the maximum possible profit found along any path in the tree.

Code Implementation

from collections import deque

def most_profitable_path(edges, bounty_amounts, alice_start_node, bob_start_node):
    number_of_nodes = len(bounty_amounts)
    adjacency_list = [[] for _ in range(number_of_nodes)]
    for start_node, end_node in edges:
        adjacency_list[start_node].append(end_node)
        adjacency_list[end_node].append(start_node)

    alice_distances = shortest_distances(number_of_nodes, adjacency_list, alice_start_node)
    bob_distances = shortest_distances(number_of_nodes, adjacency_list, bob_start_node)

    profit_amounts = [0] * number_of_nodes
    for node_index in range(number_of_nodes):
        if alice_distances[node_index] < bob_distances[node_index]:
            profit_amounts[node_index] = bounty_amounts[node_index]
        elif alice_distances[node_index] > bob_distances[node_index]:
            profit_amounts[node_index] = 0
        else:
            profit_amounts[node_index] = bounty_amounts[node_index] // 2

    # We begin at node 0
    max_profit = find_max_profit_path(adjacency_list, profit_amounts, 0, -1)
    return max_profit

def shortest_distances(number_of_nodes, adjacency_list, start_node):
    distances = [-1] * number_of_nodes
    distances[start_node] = 0
    queue = deque([start_node])

    while queue:
        current_node = queue.popleft()
        for neighbor_node in adjacency_list[current_node]:
            if distances[neighbor_node] == -1:
                distances[neighbor_node] = distances[current_node] + 1
                queue.append(neighbor_node)

    return distances

def find_max_profit_path(adjacency_list, profit_amounts, current_node, parent_node):
    max_path_profit = -float('inf')
    is_leaf = True
    # Explore neighbors, excluding the path we came from.
    for neighbor_node in adjacency_list[current_node]:
        if neighbor_node != parent_node:
            is_leaf = False

            # Accumulate profit recursively.
            path_profit = find_max_profit_path(adjacency_list, profit_amounts, neighbor_node, current_node)
            max_path_profit = max(max_path_profit, path_profit)

    # Handle leaf nodes to determine the end of this path.
    if is_leaf:
        return profit_amounts[current_node]
    else:
        # Select max of path or subtree and accumulate profit.
        return profit_amounts[current_node] + max_path_profit

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n) – Finding the shortest paths for Alice and Bob to all nodes using Breadth-First Search (BFS) takes O(n) time each, where n is the number of nodes in the tree. Traversing the tree to calculate profits also takes O(n) time since we visit each node at most once. The dominant operation is thus the traversal, making the overall time complexity O(n).

Space Complexity

O(N) – The algorithm uses extra space to store shortest distances from Alice and Bob to all N nodes in the tree, requiring two arrays of size N. The path from the root is explored using recursion, which can, in the worst-case (a skewed tree), lead to a recursion depth of N. Therefore, the space complexity is dominated by the distance arrays and the potential call stack, resulting in O(N) space.

Edge Cases

Case	How to Handle
Null or empty tree (no nodes)	Return 0 immediately, as there's no path to traverse.
Single node tree (only root node)	Return the value of the root node as the only possible profit.
Tree with all edge values as zero	The algorithm should still function correctly, returning the sum of node values along the most profitable path.
Tree with only negative edge values	The algorithm should correctly identify the path with the least negative sum (closest to zero).
Tree with very large number of nodes (maximum size constraints)	Ensure the solution uses a space and time-efficient approach (e.g., avoid unnecessary data duplication or exponential time complexity).
Deeply skewed tree (highly unbalanced)	Iterative DFS or BFS should be used to prevent stack overflow issues from excessive recursion depth.
Root has no children	The algorithm should handle this case gracefully, typically ending the path at the root and calculating profit based on root's value.
Integer overflow when calculating the path profit	Use long data type or consider modular arithmetic, depending on constraints, to prevent integer overflow during summation.