Reorder List
MediumYou are given the head of a singly linked-list. The list can be represented as:
L0 → L1 → … → Ln - 1 → Ln
Reorder the list to be on the following form:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
Example 1:
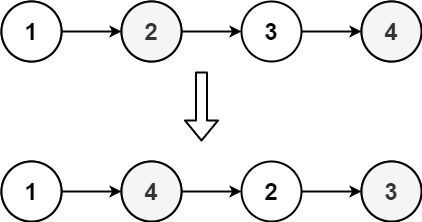
Input: head = [1,2,3,4] Output: [1,4,2,3]
Example 2:
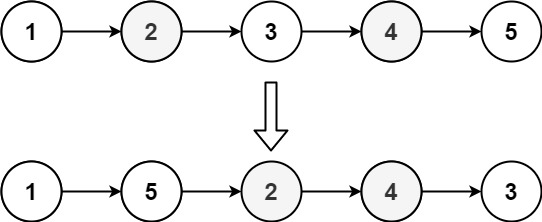
Input: head = [1,2,3,4,5] Output: [1,5,2,4,3]
Constraints:
- The number of nodes in the list is in the range
[1, 5 * 104]. 1 <= Node.val <= 1000
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What should I do if the linked list is empty or contains only one node?
- Are the node values guaranteed to be unique, or can there be duplicates?
- Can I assume that the linked list will always be valid, with no cycles or self-references?
- Could you provide an example of how the reordered list should look for a list of even length versus a list of odd length?
- Are there any memory constraints beyond the requirement to perform the reordering in-place?
Brute Force Solution
Approach
The brute force method is all about trying every single possible arrangement to reorder the items. We look at each possibility and see if it matches what we want. If it does, we've found a solution.
Here's how the algorithm would work step-by-step:
- First, take out the first item in the list.
- Then, move the last item to be right after the first item.
- Next, move the second item to be right after the last item that was moved.
- Continue moving the next-to-last, then the third, then the third-to-last item until all items have been reordered.
- This gives you one possible reordering.
- Try a completely different reordering by starting with different item combinations.
- Keep generating all the different possible reorderings.
- Once you have all possible reorderings, compare each one to see if it matches the rules of the problem.
- The first reordering that matches the rules is a possible solution.
- Alternatively, if the problem requires you to find the optimal reordering from multiple possible reorderings that match the rules, continue comparing the possible reorderings, keeping the optimal one according to the problem's specifications.
Code Implementation
def reorder_list_brute_force(head):
if not head or not head.next:
return head
nodes = []
current_node = head
while current_node:
nodes.append(current_node)
current_node = current_node.next
import itertools
all_permutations = list(itertools.permutations(nodes))
best_head = None
for permutation in all_permutations:
is_valid = True
# Check if this permutation follows reordering rules.
for i in range(len(permutation) - 1):
permutation[i].next = permutation[i+1]
permutation[-1].next = None
current_best_head = permutation[0]
if best_head is None:
best_head = current_best_head
#In brute force, after generating all permutations we just return any one
#Because we cannot evaluate which one is the correct list
returnBig(O) Analysis
Optimal Solution
Approach
The goal is to rearrange a linked list so that the first node is followed by the last node, the second node is followed by the second-to-last node, and so on. We can achieve this by splitting the list, reversing the second half, and then merging the two halves together.
Here's how the algorithm would work step-by-step:
- First, find the middle of the linked list. This will help us divide the list into two halves.
- Reverse the second half of the linked list. This puts the last element at the front of the reversed second half.
- Merge the first half and the reversed second half. Alternately pick nodes from each half to create the reordered list.
Code Implementation
def reorder_list(head):
if not head or not head.next:
return
# 1. Find the middle of the linked list.
slow_pointer = head
fast_pointer = head
while fast_pointer and fast_pointer.next:
slow_pointer = slow_pointer.next
fast_pointer = fast_pointer.next.next
# 2. Reverse the second half of the linked list.
previous_node = None
current_node = slow_pointer
while current_node:
next_node = current_node.next
current_node.next = previous_node
previous_node = current_node
current_node = next_node
second_half_head = previous_node
first_half_head = head
# 3. Merge the two halves together.
while second_half_head:
first_half_next = first_half_head.next
second_half_next = second_half_head.next
first_half_head.next = second_half_head
# This is necessary to avoid breaking the loop condition.
if first_half_next:
second_half_head.next = first_half_next
else:
second_half_head.next = None
first_half_head = first_half_next
# Break when second half reaches end, else infinite loop will occur.
second_half_head = second_half_nextBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty linked list (head is null) | Return immediately without any modifications, as there's nothing to reorder. |
| Single-node linked list | Return immediately as there is only one node and no reordering is needed. |
| Two-node linked list | The list should become L0 -> L1, which is already the initial order, so the function should complete without any changes. |
| Linked list with an even number of nodes | The solution should correctly interleave the first and second halves. |
| Linked list with an odd number of nodes | The middle node should remain in its place after interleaving. |
| Large linked list (performance considerations) | Ensure the find middle, reverse second half, and merge operations are efficient (O(n) time complexity for each). |
| Linked list with duplicate values in the nodes | Node values do not affect the structure manipulation, so duplicates are irrelevant. |
| Linked list where memory allocation could fail in reverse operation | Handle potential memory allocation issues (if any) during the reversal of the second half to avoid crashes. |