All Nodes Distance K in Binary Tree
MediumGiven the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.
You can return the answer in any order.
Example 1:
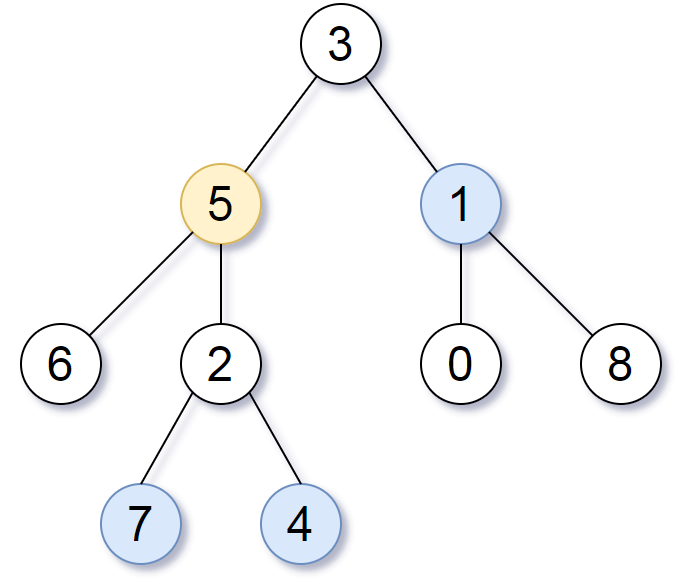
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2 Output: [7,4,1] Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
Example 2:
Input: root = [1], target = 1, k = 3 Output: []
Constraints:
- The number of nodes in the tree is in the range
[1, 500]. 0 <= Node.val <= 500- All the values
Node.valare unique. targetis the value of one of the nodes in the tree.0 <= k <= 1000
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the node data within the binary tree?
- Can the target node be null, or guaranteed to exist in the tree?
- What should I return if no nodes are exactly distance K from the target node?
- Are node values unique within the binary tree, or can duplicates exist?
- Is the input a valid binary tree, or do I need to handle cases where it might be malformed?
Brute Force Solution
Approach
The goal is to find all tree nodes that are a specific distance away from a target node. The brute force method explores the entire tree multiple times to achieve this. It involves figuring out the distance from every single node to both the target node and then checking if the distance matches the target distance.
Here's how the algorithm would work step-by-step:
- First, find the location of the target node within the tree.
- Then, starting from the root of the tree, determine the distance between every other node in the tree and the target node.
- To find these distances, explore every possible path from each node to the target node.
- For each node, if the distance to the target node matches the specified distance, add that node to our list of results.
- Repeat this process for every single node in the tree to make sure we haven't missed anything.
- Finally, after exploring all nodes and paths, return the list of nodes that are exactly the target distance away from the initial target node.
Code Implementation
def all_nodes_distance_k_brute_force(root, target, k_distance):
target_node = find_target_node(root, target.val)
result = []
all_nodes = get_all_nodes(root)
for node in all_nodes:
distance = distance_between_nodes(node, target_node)
# Only add to result if the distance equals to target distance
if distance == k_distance:
result.append(node)
return result
def find_target_node(root, target_value):
if not root:
return None
if root.val == target_value:
return root
left_result = find_target_node(root.left, target_value)
if left_result:
return left_result
return find_target_node(root.right, target_value)
def get_all_nodes(root):
if not root:
return []
return [root] + get_all_nodes(root.left) + get_all_nodes(root.right)
def distance_between_nodes(node1, node2):
if node1 == node2:
return 0
# Explore all possible paths to find the shortest distance
queue = [(node1, 0)]
visited = {node1}
while queue:
current_node, current_distance = queue.pop(0)
if current_node == node2:
return current_distance
neighbors = get_neighbors(current_node)
for neighbor in neighbors:
if neighbor and neighbor not in visited:
queue.append((neighbor, current_distance + 1))
visited.add(neighbor)
return float('inf')
def get_neighbors(node):
neighbors = []
if node.left:
neighbors.append(node.left)
if node.right:
neighbors.append(node.right)
# Assuming each node does not have a parent
return neighborsBig(O) Analysis
Optimal Solution
Approach
The problem asks us to find all nodes at a certain distance from a given target node in a binary tree. The key insight is to treat the tree as a graph and perform a breadth-first search (BFS) starting from the target, but we need to know the parent of each node.
Here's how the algorithm would work step-by-step:
- First, transform the binary tree into a graph where each node also knows its parent. This will let us move both up and down the tree during our search.
- Use a standard breadth-first search algorithm, starting at the target node.
- Keep track of the distance from the target node as you explore outwards.
- At each node, check its left child, right child, and parent (if it exists and hasn't been visited yet).
- Continue the breadth-first search until you reach the desired distance from the target.
- Collect all the nodes at that distance. These are the nodes that meet the criteria of the question.
- The conversion to a graph allows the flexibility to go up and down the tree, and BFS guarantees you find nodes at distance K while visiting the fewest nodes possible.
Code Implementation
import collections
def all_nodes_distance_k(root, target, k):
parent_map = {}
def dfs(node, parent):
if node:
parent_map[node] = parent
dfs(node.left, node)
dfs(node.right, node)
dfs(root, None)
# BFS to find nodes at distance K from the target.
queue = collections.deque([(target, 0)])
seen = {target}
result = []
while queue:
node, distance = queue.popleft()
if distance == k:
result.append(node.val)
continue
# Check neighbors: left, right, and parent.
for neighbor in [node.left, node.right, parent_map[node]]:
# Only process unvisited neighbors.
if neighbor and neighbor not in seen:
seen.add(neighbor)
queue.append((neighbor, distance + 1))
return resultBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node | Return an empty list immediately as there are no nodes in the tree. |
| Target node is the root node and K is 0 | Return a list containing only the root node's value. |
| Target node is the root node and K is greater than 0 | Perform BFS/DFS from root to find nodes at distance K. |
| K is 0 and target node is not the root | Return a list containing only the target node's value. |
| K is larger than the maximum possible distance from target to any node in the tree | Return an empty list if no nodes are at distance K. |
| Tree is a skewed tree (all nodes on one side) | The graph construction and BFS/DFS should handle skewed trees correctly, potentially affecting performance. |
| Target node does not exist in the tree | Return an empty list if the target node is not found during the initial search. |
| Tree contains duplicate values, and there are multiple nodes that equal the target value | The algorithm should be modified to handle multiple target nodes, which may require finding the distances from each occurrence and then deduplicating the result. |