Check if a Parentheses String Can Be Valid
MediumA parentheses string is a non-empty string consisting only of '(' and ')'. It is valid if any of the following conditions is true:
- It is
(). - It can be written as
AB(Aconcatenated withB), whereAandBare valid parentheses strings. - It can be written as
(A), whereAis a valid parentheses string.
You are given a parentheses string s and a string locked, both of length n. locked is a binary string consisting only of '0's and '1's. For each index i of locked,
- If
locked[i]is'1', you cannot changes[i]. - But if
locked[i]is'0', you can changes[i]to either'('or')'.
Return true if you can make s a valid parentheses string. Otherwise, return false.
Example 1:
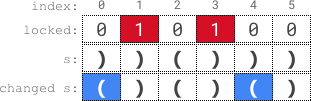
Input: s = "))()))", locked = "010100"
Output: true
Explanation: locked[1] == '1' and locked[3] == '1', so we cannot change s[1] or s[3].
We change s[0] and s[4] to '(' while leaving s[2] and s[5] unchanged to make s valid.
Example 2:
Input: s = "()()", locked = "0000" Output: true Explanation: We do not need to make any changes because s is already valid.
Example 3:
Input: s = ")", locked = "0"
Output: false
Explanation: locked permits us to change s[0].
Changing s[0] to either '(' or ')' will not make s valid.
Example 4:
Input: s = "(((())(((())", locked = "111111010111" Output: true Explanation: locked permits us to change s[6] and s[8]. We change s[6] and s[8] to ')' to make s valid.
Constraints:
n == s.length == locked.length1 <= n <= 105s[i]is either'('or')'.locked[i]is either'0'or'1'.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What characters besides '(' and ')' might be present in the input string, and how should I handle them?
- How long can the input string `s` and the locked string `locked` be? Is there a reasonable upper bound?
- If the string `s` is empty, what should I return?
- If it's impossible to make `s` valid, should I return false or is there another error condition I should signal?
- Does the `locked` string always have the same length as the input string `s`?
Brute Force Solution
Approach
The brute force method for this parenthesis problem means we'll try every single combination of opening and closing parentheses to see if it's valid. We essentially generate all possible strings using the given allowed modifications and then check if each one works. This guarantees we find the solution, but it will likely take a long time.
Here's how the algorithm would work step-by-step:
- Consider all possible arrangements where we can change the asterisk characters into either opening parentheses, closing parentheses, or leave them blank.
- For each of these arrangements, check if the parentheses are balanced. A balanced arrangement means that for every closing parenthesis, there is a corresponding opening parenthesis before it, and the total number of opening parentheses equals the total number of closing parentheses.
- If an arrangement is balanced according to these rules, then it is a valid parentheses string.
- After checking all the arrangements, if we find at least one valid string, then the original string can be made valid. Otherwise, it cannot.
Code Implementation
def check_if_string_can_be_valid_brute_force(parentheses_string):
asterisk_indices = [index for index, char in enumerate(parentheses_string) if char == '*']
number_of_asterisks = len(asterisk_indices)
# Iterate through all possible combinations of replacing asterisks
for i in range(3 ** number_of_asterisks):
temp_index = i
modified_string_list = list(parentheses_string)
# Convert the base-3 representation to parentheses choices
for asterisk_index in asterisk_indices:
remainder = temp_index % 3
temp_index //= 3
if remainder == 0:
modified_string_list[asterisk_index] = '('
elif remainder == 1:
modified_string_list[asterisk_index] = ')'
else:
modified_string_list[asterisk_index] = ''
modified_string = "".join(modified_string_list)
# Check if the modified string is valid
if is_valid_parentheses_string(modified_string):
return True
return False
def is_valid_parentheses_string(modified_string):
balance = 0
# Check if parenthesis string is balanced
for char in modified_string:
if char == '(':
balance += 1
elif char == ')':
balance -= 1
# Early exit if unbalanced
if balance < 0:
return False
# String is valid if balance is 0
return balance == 0Big(O) Analysis
Optimal Solution
Approach
The goal is to determine if a string of parentheses can be made valid with certain positions allowed to be flipped. The optimal strategy uses two counters to track the balance of open and close parentheses from both left to right, and right to left, making sure you have enough 'free flips' to correct any imbalances.
Here's how the algorithm would work step-by-step:
- Start by counting parentheses from left to right, keeping track of the 'balance' (open minus close).
- Also, keep track of how many positions you are allowed to flip to change an open parenthesis to closed, or vice versa.
- If you encounter a situation where you have more close parentheses than open parentheses, use one of your 'allowed flips' to fix it, but only if you have any available.
- If you run out of 'allowed flips' before you can fix the imbalance, the string cannot be made valid.
- Repeat the process, but now going from right to left.
- This time, count the balance as 'close minus open', and again use the 'allowed flips' to correct imbalances.
- If both passes (left to right, and right to left) are successful in reaching the end of the string without running out of 'allowed flips', then the string can be made valid.
Code Implementation
def can_be_valid(parentheses_string, locked_string):
string_length = len(parentheses_string)
if string_length % 2 != 0:
return False
modifiable_count = 0
balance = 0
for i in range(string_length):
if locked_string[i] == '0':
modifiable_count += 1
elif parentheses_string[i] == '(':
balance += 1
else:
balance -= 1
# Correct imbalance with flips
if balance < 0:
if modifiable_count > 0:
modifiable_count -= 1
balance += 1
else:
return False
modifiable_count = 0
balance = 0
for i in range(string_length - 1, -1, -1):
if locked_string[i] == '0':
modifiable_count += 1
elif parentheses_string[i] == ')':
balance += 1
else:
balance -= 1
# Correct imbalance with flips
if balance < 0:
if modifiable_count > 0:
modifiable_count -= 1
balance += 1
else:
return False
# After both passes, string is valid
return TrueBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty input string | Return true if the string is null or empty as an empty string is considered valid |
| String with only opening parentheses or only closing parentheses | The balancing logic should identify and return false, as these cannot form valid pairs. |
| String with an odd number of characters | Immediately return false, since a valid parentheses string must have an even number of characters. |
| String with mismatched parentheses and a locked string with only 1's | Even if all characters are 'locked', if parentheses aren't balanced, return false. |
| String with many '0's in the locked string which allows a flexible solution, but is impossible | The algorithm should account for the flexibility and ensure that a valid solution can still not be obtained. |
| String with nested parentheses of varying depths | The balancing logic should handle arbitrary nesting correctly, so deep nesting is not a problem |
| Very large input string | Ensure the solution has linear time complexity and does not consume excessive memory to prevent timeouts or out-of-memory errors. |
| Locked string with more open parentheses than allowed by unlocked characters | Track locked counts separately and if it becomes impossible to balance, return false. |