Smallest Subtree with all the Deepest Nodes
MediumGiven the root of a binary tree, the depth of each node is the shortest distance to the root.
Return the smallest subtree such that it contains all the deepest nodes in the original tree.
A node is called the deepest if it has the largest depth possible among any node in the entire tree.
The subtree of a node is a tree consisting of that node, plus the set of all descendants of that node.
Example 1:
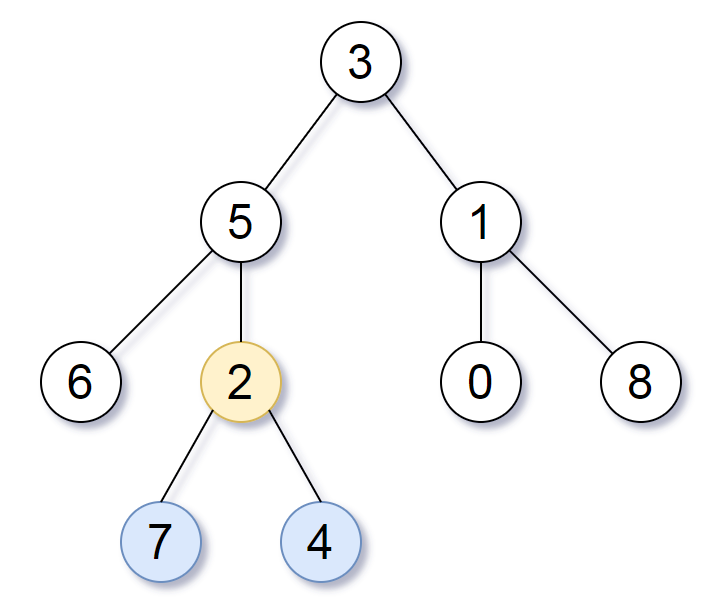
Input: root = [3,5,1,6,2,0,8,null,null,7,4] Output: [2,7,4] Explanation: We return the node with value 2, colored in yellow in the diagram. The nodes coloured in blue are the deepest nodes of the tree. Notice that nodes 5, 3 and 2 contain the deepest nodes in the tree but node 2 is the smallest subtree among them, so we return it.
Example 2:
Input: root = [1] Output: [1] Explanation: The root is the deepest node in the tree.
Example 3:
Input: root = [0,1,3,null,2] Output: [2] Explanation: The deepest node in the tree is 2, the valid subtrees are the subtrees of nodes 2, 1 and 0 but the subtree of node 2 is the smallest.
Constraints:
- The number of nodes in the tree will be in the range
[1, 500]. 0 <= Node.val <= 500- The values of the nodes in the tree are unique.
Note: This question is the same as 1123: https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the tree be empty, or contain only a single node?
- What is the structure of the `TreeNode`? Specifically, what are the names and types of its attributes (e.g., `val`, `left`, `right`)?
- If there are multiple subtrees that qualify as the smallest subtree containing all the deepest nodes, which one should I return? Is there a specific tie-breaking condition?
- What is the range of values for the node values in the tree? Are they integers?
- What should I return if all nodes are at the same depth?
Brute Force Solution
Approach
To find the smallest part of the tree containing all the deepest points, we'll explore every possible section of the tree. We'll methodically check each section to see if it holds all the deepest points, and if it's smaller than any section we've checked so far.
Here's how the algorithm would work step-by-step:
- First, figure out what the deepest level in the whole tree is.
- Then, identify all the points (nodes) that are at that deepest level.
- Now, consider every single point in the tree as a potential starting point for our section.
- For each starting point, check if the section of the tree starting from that point includes all the deepest points we found earlier.
- If a section does contain all the deepest points, remember it. Also remember how big that section is.
- Keep doing this for every point in the tree. Each time you find a section that has all the deepest points and is smaller than the smallest one you've found so far, replace the one you remember with the new, smaller one.
- After checking every single point in the tree, the section you remembered at the end will be the smallest section that contains all the deepest points.
Code Implementation
def subtree_with_all_deepest(root):
def find_deepest_level(node, level, deepest_level):
if not node:
return deepest_level
deepest_level[0] = max(deepest_level[0], level)
deepest_level = find_deepest_level(node.left, level + 1, deepest_level)
deepest_level = find_deepest_level(node.right, level + 1, deepest_level)
return deepest_level
def find_deepest_nodes(node, level, deepest_level, deepest_nodes):
if not node:
return
if level == deepest_level[0]:
deepest_nodes.append(node)
return
find_deepest_nodes(node.left, level + 1, deepest_level, deepest_nodes)
find_deepest_nodes(node.right, level + 1, deepest_level, deepest_nodes)
def contains_all_deepest(subtree_root, deepest_nodes):
found_nodes = []
def traverse(node):
if not node:
return
if node in deepest_nodes:
found_nodes.append(node)
traverse(node.left)
traverse(node.right)
traverse(subtree_root)
# Make sure we found all the deepest nodes
return len(found_nodes) == len(deepest_nodes)
deepest_level = [0]
find_deepest_level(root, 0, deepest_level)
deepest_nodes = []
find_deepest_nodes(root, 0, deepest_level, deepest_nodes)
smallest_subtree = None
smallest_subtree_size = float('inf')
def get_subtree_size(node):
if not node:
return 0
return 1 + get_subtree_size(node.left) + get_subtree_size(node.right)
def check_all_nodes(node):
nonlocal smallest_subtree, smallest_subtree_size
if not node:
return
# Check if this node's subtree contains all deepest nodes
if contains_all_deepest(node, deepest_nodes):
subtree_size = get_subtree_size(node)
# If so, see if it's smaller than the current smallest
if subtree_size < smallest_subtree_size:
smallest_subtree = node
smallest_subtree_size = subtree_size
check_all_nodes(node.left)
check_all_nodes(node.right)
# Iterate through all the nodes and check
check_all_nodes(root)
return smallest_subtreeBig(O) Analysis
Optimal Solution
Approach
The goal is to find the smallest part of the tree that contains all the deepest parts. We figure this out by working our way up from the bottom, understanding the depth of each part of the tree.
Here's how the algorithm would work step-by-step:
- First, find out how deep the tree goes. We need to know what the 'deepest' level actually is.
- Next, look at each part of the tree, starting from the bottom. For each part, figure out if it contains any of the deepest parts. Also, find out how deep those deepest parts are inside that part of the tree.
- If a part of the tree has some of the deepest parts, we'll keep track of it and its depth. If it doesn't have any of the deepest parts, we'll ignore it.
- As we move up the tree, we'll notice that some parts contain all of the deepest parts. The smallest of these parts is our answer. If a part contains the deepest parts, but its own smaller parts also contain them, we pick the smaller parts instead.
- Eventually, we'll reach the very top of the tree. By then, we'll have found the smallest part that includes all the deepest parts. That's the answer we're looking for.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
def subtree_with_all_deepest(root):
def depth(node):
if not node:
return 0
return 1 + max(depth(node.left), depth(node.right))
deepest_level = depth(root)
def deepest_subtree_helper(node, current_depth):
if not node:
return None, 0
left_subtree, left_depth = deepest_subtree_helper(node.left, current_depth + 1)
right_subtree, right_depth = deepest_subtree_helper(node.right, current_depth + 1)
# Found deepest level node
if current_depth == deepest_level:
return node, current_depth
if left_depth == right_depth:
# If both subtrees have deepest nodes, current node has all deepest nodes
if left_depth > 0:
return node, left_depth
else:
return None, 0
# Propagate the subtree with deepest nodes.
if left_depth > right_depth:
return left_subtree, left_depth
else:
return right_subtree, right_depth
result_subtree, result_depth = deepest_subtree_helper(root, 1)
return result_subtreeBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree root | Return null immediately since an empty tree has no smallest subtree. |
| Tree with only one node (root) | Return the root node itself, as it's the deepest and only node. |
| All nodes are at the same depth (perfect tree) | The root is the smallest subtree containing all deepest nodes, so return the root. |
| Skewed tree (all nodes on one branch) | The deepest node is at the end of the branch, and the smallest subtree is the deepest node itself. |
| Very large tree causing stack overflow if using recursion naively | Use an iterative approach like BFS or DFS with explicit stack management to avoid exceeding the stack limit. |
| Tree with multiple nodes at the deepest level spanning across subtrees | The algorithm should correctly identify the common ancestor containing all deepest nodes regardless of distribution. |
| Tree with duplicate values that might affect depth calculation | The depth calculation should be based on the path from the root, not the value of the nodes. |
| Integer overflow in calculating depths if the tree is extremely deep | Use a larger data type like long or consider that depths usually don't require to be very high with respect to memory limits. |