Average of Levels in Binary Tree
Easyroot of a binary tree, return the average value of the nodes on each level in the form of an array. Answers within 10-5 of the actual answer will be accepted.
Example 1:
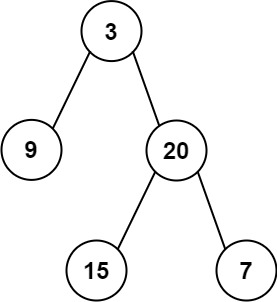
Input: root = [3,9,20,null,null,15,7] Output: [3.00000,14.50000,11.00000] Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11. Hence return [3, 14.5, 11].
Example 2:
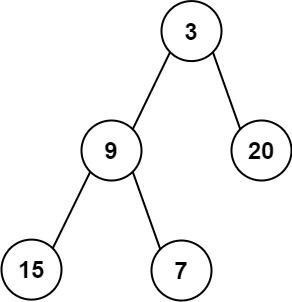
Input: root = [3,9,20,15,7] Output: [3.00000,14.50000,11.00000]
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. -231 <= Node.val <= 231 - 1
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the nodes in the binary tree, and can they be negative or floating-point numbers?
- What should I return if the input `root` is null or represents an empty tree? Should I return an empty list, or is there a specific value expected?
- Is the binary tree guaranteed to be a complete binary tree, or can it be unbalanced?
- Are there any memory constraints I should consider, given that I might need to store the nodes at each level during the traversal?
- For floating-point averages, what level of precision is required in the output list? Are there specific rounding rules to adhere to?
Brute Force Solution
Approach
The brute force approach to finding the average value at each level of a binary tree involves visiting every single level in the tree. We calculate the sum of all values present at each level. After the sum is calculated, we divide it by the count of nodes at that level to find the average.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, which is level zero.
- Go through the tree level by level. At each level, add up the values of all the 'nodes' you find there.
- Count how many 'nodes' there are at each level.
- For each level, divide the sum of the values by the number of 'nodes' you counted. This gives you the average value for that level.
- Do this for every level of the tree, from top to bottom.
- Record the average value for each level.
Code Implementation
def average_of_levels(root):
if not root:
return []
level_averages = []
nodes_queue = [root]
while nodes_queue:
level_length = len(nodes_queue)
level_sum = 0
# Iterate over all nodes in current level
for _ in range(level_length):
node = nodes_queue.pop(0)
level_sum += node.val
# Add children to queue for next level
if node.left:
nodes_queue.append(node.left)
if node.right:
nodes_queue.append(node.right)
# Calculate average and record it for level
average = float(level_sum) / level_length
level_averages.append(average)
return level_averagesBig(O) Analysis
Optimal Solution
Approach
To find the average value at each level of a binary tree efficiently, we'll visit each level one by one. We'll keep a running sum of the node values and count how many nodes are at that level so we can find the average.
Here's how the algorithm would work step-by-step:
- Begin with the very top level of the tree, which only includes the single root node.
- Create a 'to do' list that initially contains only the root node.
- While there are levels left 'to do' (meaning our 'to do' list isn't empty):
- Calculate the sum of all the node values on the current level.
- Count how many nodes are on this level.
- Compute the average for the level by dividing the sum by the count.
- Prepare the 'to do' list for the next level by gathering all the children of the nodes from the current level.
- Record the average and repeat the process for the next level.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def averageOfLevels(root):
levels_averages = []
nodes_to_do = [root]
# Process each level of the tree
while nodes_to_do:
level_sum = 0
level_size = 0
next_level_nodes = []
# Iterate through the nodes at the current level
for node in nodes_to_do:
level_sum += node.val
level_size += 1
# Add children to the queue for the next level
if node.left:
next_level_nodes.append(node.left)
if node.right:
next_level_nodes.append(node.right)
# Store average value for the current level
average = float(level_sum) / level_size
levels_averages.append(average)
# Update the queue for the next level traversal.
nodes_to_do = next_level_nodes
return levels_averagesBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree (root is null) | Return an empty list immediately since there are no levels to average. |
| Tree with only one node (root only) | Return a list containing only the root's value as the average of level 0. |
| Tree with all nodes having the same value. | The average at each level will be the same as the node value, handled correctly by level order traversal. |
| Tree with very large or very small node values, leading to potential integer overflow during sum calculation at a level. | Use long or double to store the sum of node values at each level to prevent overflow. |
| Highly skewed tree (e.g., all nodes on one branch) | The level order traversal still works correctly, averaging only the node at each level. |
| Tree with a very large number of levels, potentially exceeding stack space if using recursion. | Use iterative level order traversal (BFS) to avoid stack overflow errors. |
| Floating-point precision issues when calculating the average. | Use double to store the average and be aware of potential minor inaccuracies. |
| Negative node values. | The average calculation will handle negative values correctly as part of the sum. |