Leaf-Similar Trees
EasyConsider all the leaves of a binary tree, from left to right order, the values of those leaves form a leaf value sequence.
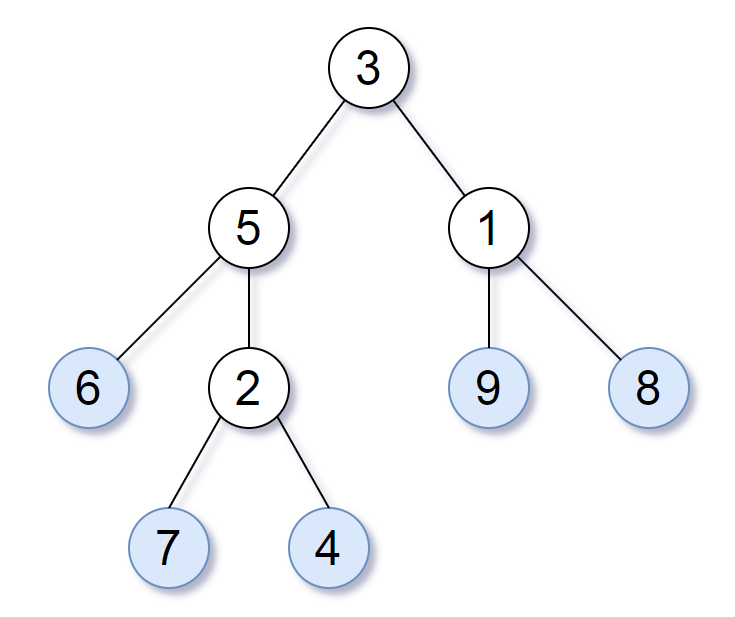
For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8).
Two binary trees are considered leaf-similar if their leaf value sequence is the same.
Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.
Example 1:
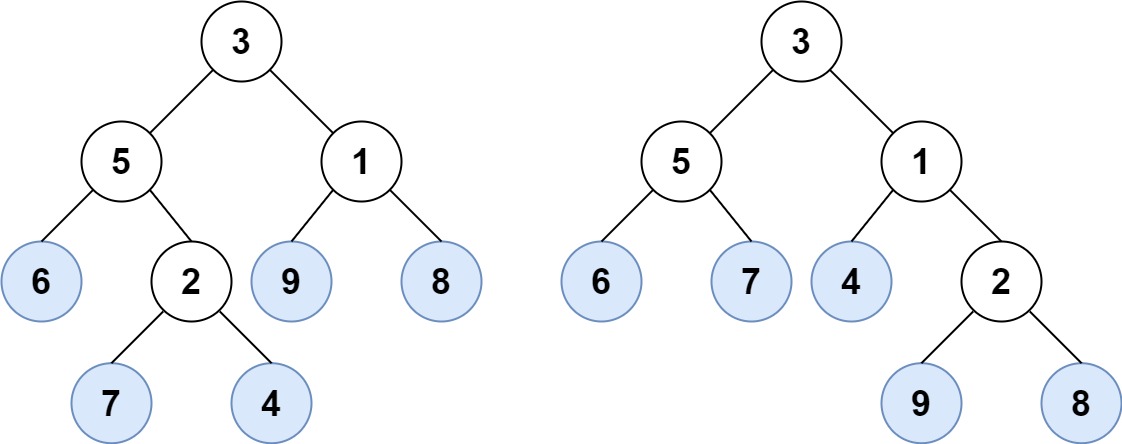
Input: root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8] Output: true
Example 2:
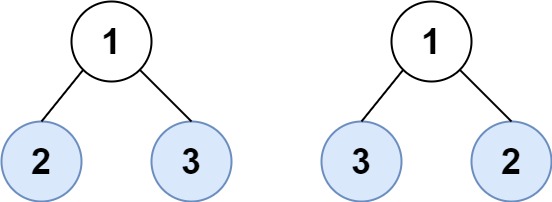
Input: root1 = [1,2,3], root2 = [1,3,2] Output: false
Constraints:
- The number of nodes in each tree will be in the range
[1, 200]. - Both of the given trees will have values in the range
[0, 200].
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the nodes in the trees? Can node values be negative, zero, or floating-point numbers?
- Could either of the input trees be empty or null? If so, how should I handle that case?
- Are the trees guaranteed to be valid binary trees, or do I need to handle cases with cycles or other invalid tree structures?
- Does the order of the leaf values within each tree's leaf sequence matter, or only the presence of specific values?
- Are we aiming for a specific time or space complexity, or should I optimize for both if possible?
Brute Force Solution
Approach
To determine if two trees are leaf-similar using brute force, we essentially extract the sequence of leaves from each tree separately. Then, we directly compare these two sequences to see if they are identical.
Here's how the algorithm would work step-by-step:
- First, for the first tree, we need to find all its leaves and record them in the order we encounter them from left to right.
- We do this by systematically visiting every part of the tree and keeping track of the leaves.
- Next, we do the same thing for the second tree. Find all of its leaves and record them in the same order.
- Now that we have two sequences, one for each tree, we just compare them to see if they are the same.
- If the sequences are exactly the same, then the trees are leaf-similar. If not, they are not.
Code Implementation
def leaf_similar(root_one, root_two):
def get_leaf_sequence(root):
leaf_nodes = []
def dfs(node):
if not node:
return
if not node.left and not node.right:
# Node is a leaf, add its value to the sequence.
leaf_nodes.append(node.val)
return
dfs(node.left)
dfs(node.right)
dfs(root)
return leaf_nodes
# Extract leaf sequence from the first tree.
leaf_sequence_one = get_leaf_sequence(root_one)
# Extract leaf sequence from the second tree.
leaf_sequence_two = get_leaf_sequence(root_two)
# Compare the two leaf sequences to check for similarity.
return leaf_sequence_one == leaf_sequence_twoBig(O) Analysis
Optimal Solution
Approach
The most efficient way to check if two trees are leaf-similar is to find all the leaves of each tree and then compare the order in which they appear. We achieve this by walking through each tree and extracting just the leaf values in the order we encounter them.
Here's how the algorithm would work step-by-step:
- Define what a 'leaf' is: a node with no children.
- For the first tree, go all the way down the left side as far as possible. When you get to a dead end, go back one step and check its right side, and so on. Extract the leaf values in the order you find them.
- Repeat this process for the second tree and extract its leaf values, again preserving the order in which you find them.
- Compare the two lists of leaf values. If the lists are identical (same values in the same order), then the trees are leaf-similar.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def leaf_similar(root1, root2):
def get_leaf_sequence(root):
leaf_nodes = []
def dfs(node):
if not node:
return
# Check if node is leaf.
if not node.left and not node.right:
leaf_nodes.append(node.val)
return
dfs(node.left)
dfs(node.right)
dfs(root)
return leaf_nodes
# Extract leaf sequences for both trees.
leaf_sequence_root1 = get_leaf_sequence(root1)
leaf_sequence_root2 = get_leaf_sequence(root2)
# Compare the two leaf sequences.
return leaf_sequence_root1 == leaf_sequence_root2Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Both trees are null | Return true, as they are considered leaf-similar. |
| One tree is null, the other is not | Return false, as they cannot be leaf-similar. |
| Both trees have only one node (root) | Check if their values are the same, return true if they are, false otherwise. |
| One tree has only one leaf node, the other has multiple leaf nodes. | The leaf sequences will have different lengths, resulting in a false return. |
| Trees are very large and deep, potentially causing stack overflow with recursive solutions. | Consider iterative solutions (e.g., using a stack) to avoid exceeding recursion depth limits. |
| Trees have identical leaf value sequences. | The algorithm should correctly identify them as leaf-similar and return true. |
| Trees have leaf nodes with negative values or zero. | The solution must handle these values correctly without errors. |
| One or both trees are highly unbalanced or skewed. | Ensure algorithm correctly traverses and extracts the leaf sequence regardless of tree structure. |