Number of Operations to Make Network Connected

Medium

Nvidia

0 views

Topics:

GraphsDynamic Programming

There are n computers numbered from 0 to n - 1 connected by ethernet cables connections forming a network where connections[i] = [a_i, b_i] represents a connection between computers a_i and b_i. Any computer can reach any other computer directly or indirectly through the network.

You are given an initial computer network connections. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.

Return the minimum number of times you need to do this in order to make all the computers connected. If it is not possible, return -1.

Example 1:

Input: n = 4, connections = [[0,1],[0,2],[1,2]]
Output: 1
Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.

Example 2:

Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
Output: 2

Example 3:

Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
Output: -1
Explanation: There are not enough cables.

Constraints:

1 <= n <= 10⁵
1 <= connections.length <= min(n * (n - 1) / 2, 10⁵)
connections[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
There are no repeated connections.
No two computers are connected by more than one cable.

Number of Operations to Make Network Connected

Medium

Nvidia

0 views

Topics:

GraphsDynamic Programming

There are n computers numbered from 0 to n - 1 connected by ethernet cables connections forming a network where connections[i] = [a_i, b_i] represents a connection between computers a_i and b_i. Any computer can reach any other computer directly or indirectly through the network.

You are given an initial computer network connections. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.

Return the minimum number of times you need to do this in order to make all the computers connected. If it is not possible, return -1.

Example 1:

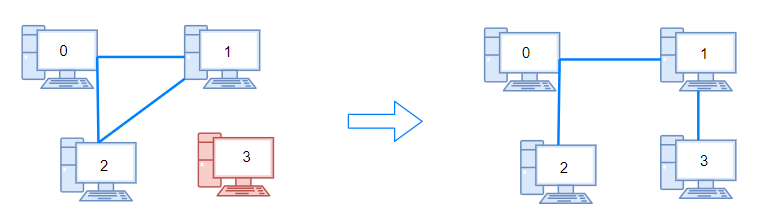
Input: n = 4, connections = [[0,1],[0,2],[1,2]]
Output: 1
Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.

Example 2:

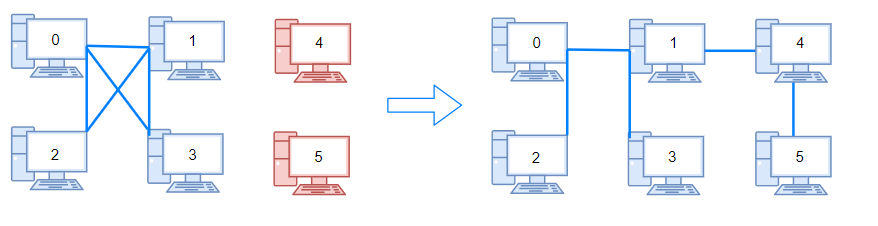
Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
Output: 2

Example 3:

Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
Output: -1
Explanation: There are not enough cables.

Constraints:

1 <= n <= 10⁵
1 <= connections.length <= min(n * (n - 1) / 2, 10⁵)
connections[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
There are no repeated connections.
No two computers are connected by more than one cable.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the maximum number of computers, n, that I should expect as input?
Are the computer labels (u and v in the connections list) zero-indexed or one-indexed?
If it is impossible to connect all computers, is -1 the *only* value I should return, or are there other conditions that would also result in a -1?
Can I assume that the connections provided in the input list are undirected (i.e., [u, v] is the same as [v, u])?
Is it possible for the connections list to contain duplicate connections (e.g., [[1, 2], [1, 2]])?

Brute Force Solution

Approach

The problem is to connect all computers in a network using cables. A brute-force approach involves trying all possible combinations of cables to see if they connect the entire network, then determining how many extra cables are needed.

Here's how the algorithm would work step-by-step:

First, try every possible way to pick a single cable and see if that connects the entire network.
If that doesn't work, then try every possible pair of cables and see if that connects the network.
Then try every possible group of three cables, then four, and so on, checking each group to see if it successfully connects the network.
For each group of cables that connects the network, count how many cables weren't used.
The smallest number of unused cables from all successful connection attempts is our answer.

Code Implementation

def number_of_operations_to_make_network_connected_brute_force(number_of_nodes, connections):
    all_cables = connections
    number_of_cables = len(all_cables)

    # Generate all possible combinations of cables
    for cable_group_size in range(1, number_of_cables + 1):
        import itertools
        for cable_group in itertools.combinations(all_cables, cable_group_size):

            # Check if the cable group connects the network
            if is_network_connected(number_of_nodes, list(cable_group)):

                # Calculate the number of unused cables
                unused_cables = number_of_cables - cable_group_size
                return unused_cables

    return -1

def is_network_connected(number_of_nodes, connections):

    # Initialize the visited array to keep track of the visited nodes
    visited_nodes = [False] * number_of_nodes
    
    # Start DFS from node 0
    depth_first_search(0, connections, visited_nodes)

    # Check if all nodes are visited
    for visited in visited_nodes:
        if not visited:
            return False
    return True

def depth_first_search(node, connections, visited_nodes):

    # Mark the current node as visited
    visited_nodes[node] = True

    # Iterate through the connections to find the neighbors
    for first_node, second_node in connections:
        if first_node == node and not visited_nodes[second_node]:
            depth_first_search(second_node, connections, visited_nodes)
        elif second_node == node and not visited_nodes[first_node]:
            depth_first_search(first_node, connections, visited_nodes)

Big(O) Analysis

Time Complexity

O((V choose 1) + (V choose 2) + ... + (V choose K) * ConnectivityCheck(V, E)) – The provided solution explores all possible combinations of cables. We are picking groups of size 1 to K from the available cables where K is less than or equal to the number of available cables V, and V is at most the number of possible connections between all nodes, which is O(N^2) where N is the number of nodes. For each such group, the algorithm must also perform a connectivity check using an algorithm with complexity ConnectivityCheck(V, E) which could be as low as O(V+E) with disjoint sets, where E is the number of edges in our picked group. The dominant factor of the time complexity is therefore the sum of all choose functions from 1 to K multiplied by ConnectivityCheck(V, E).

Space Complexity

O(n + e choose k) – The algorithm explores combinations of cables. In the worst case, it may need to store each combination of 'k' cables chosen from 'e' total cables, where 'k' can range up to 'e' leading to a combinations calculation. The algorithm also needs to determine if each tested combination connects the network. This would likely require tracking visited nodes, potentially using a data structure with a size proportional to 'n', where n is the number of computers. The space needed to track visited computers for graph traversal and cable combinations results in O(n + e choose k) space complexity, assuming the largest possible combination of edges need to be stored.

Optimal Solution

Approach

The problem asks us to connect computers in a network with the minimum number of operations. The key idea is to first check if we even have enough cables to connect all the computers and then use a technique to efficiently identify separate groups of computers.

Here's how the algorithm would work step-by-step:

First, count the total number of available cables. If we don't have enough cables to connect all computers into one network, it's impossible to connect them all, and we can stop.
Next, imagine each computer as a member of a group. Initially, each computer is in its own separate group.
We then go through the existing cables. Each cable connects two computers, so if those two computers are in different groups, we merge those groups into one. This represents connecting the computers.
After processing all the cables, we count how many separate groups are left. Each separate group represents a disconnected part of the network.
The number of operations we need is one less than the number of disconnected groups. This is because we need that many extra cables to link all the groups together into a single, connected network.

Code Implementation

def number_of_operations_to_make_network_connected(number_of_nodes, connections):
    number_of_cables = len(connections)

    if number_of_cables < number_of_nodes - 1:
        return -1

    parent = list(range(number_of_nodes))

    def find(node_id):
        if parent[node_id] != node_id:
            parent[node_id] = find(parent[node_id])
        return parent[node_id]

    def union(node_id_one, node_id_two):
        root_one = find(node_id_one)
        root_two = find(node_id_two)
        if root_one != root_two:
            parent[root_one] = root_two
            return True
        return False

    # Iterate through each connection to attempt union operations.
    for node_id_one, node_id_two in connections:
        union(node_id_one, node_id_two)

    number_of_connected_components = 0
    # Count the number of distinct connected components
    for node_id in range(number_of_nodes):
        if parent[node_id] == node_id:

            number_of_connected_components += 1

    # Need one less cable than the number of components to connect
    return number_of_connected_components - 1

Big(O) Analysis

Time Complexity

O(n + m) – The algorithm iterates through all n computers, initially assigning each to its own group which takes O(n) time. It then iterates through m cables. For each cable, it performs a find operation to determine the group of each connected computer and potentially a union operation to merge the groups if they are different. Assuming the find and union operations are nearly constant time using techniques like path compression and union by rank in a disjoint set data structure, the overall time complexity is dominated by iterating through the cables. Therefore, the algorithm runs in O(n + m) time.

Space Complexity

O(N) – The primary auxiliary space is used by the group representation, which effectively keeps track of which computer belongs to which connected component. In the worst case, this requires storing a group identifier for each of the N computers. Therefore, the auxiliary space is proportional to the number of computers, resulting in O(N) space complexity.

Edge Cases

Case	How to Handle
Null or empty connections array	If the connections array is null or empty, check if n > 1; if so return -1, otherwise 0.
n is 1 (single computer)	If n is 1, no connections are needed, so return 0 regardless of the connections array.
Insufficient number of connections to connect all computers.	If the number of connections is less than n - 1, return -1 indicating it's impossible to connect all computers.
Excessive number of redundant connections (cycles present).	The solution should correctly identify connected components and calculate redundant edges based on connected components.
Large n (number of computers) causing potential stack overflow with recursive DFS.	Use iterative DFS or Union Find to avoid potential stack overflow for large input sizes.
Input contains duplicate connections between same computers ([u, v] and [v, u] considered same).	Union Find handles duplicate connections correctly by only considering the connection once.
Inputs with all computers already connected in one component.	The algorithm should detect this and return 0 indicating no operations are needed.
Integer overflow possibility when calculating connections count or redundant cables	Use 64 bit integer types or guard against potential overflows in calculations.