Odd Even Linked List
MediumGiven the head of a singly linked list, group all the nodes with odd indices together followed by the nodes with even indices, and return the reordered list.
The first node is considered odd, and the second node is even, and so on.
Note that the relative order inside both the even and odd groups should remain as it was in the input.
You must solve the problem in O(1) extra space complexity and O(n) time complexity.
Example 1:

Input: head = [1,2,3,4,5] Output: [1,3,5,2,4]
Example 2:
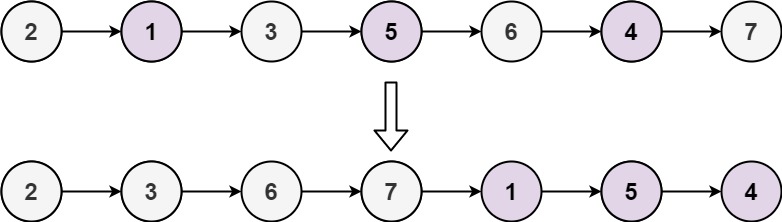
Input: head = [2,1,3,5,6,4,7] Output: [2,3,6,7,1,5,4]
Constraints:
- The number of nodes in the linked list is in the range
[0, 104]. -106 <= Node.val <= 106
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the linked list be empty, or contain only one node?
- What is the range of values for the nodes in the linked list?
- Should the relative order of nodes within the odd and even groups be exactly as they were in the original list?
- If the linked list has an odd number of nodes, will the last odd node point to the first even node?
- Is it acceptable to modify the `next` pointers of the existing nodes, or should I create new nodes?
Brute Force Solution
Approach
The brute force strategy to rearrange a linked list such that odd-numbered positions appear before even-numbered positions involves considering all possible orderings. We explore every possible rearrangement of the list's elements. We will then rearrange the actual list based on what we have found.
Here's how the algorithm would work step-by-step:
- First, create a copy of the linked list as a separate data structure that allows easy rearranging.
- Now, think of all the possible ways you could arrange the nodes within this copy.
- For each arrangement, go through the copied list and check if all the odd-positioned nodes come before all the even-positioned nodes.
- If you find an arrangement where all odd-positioned nodes are indeed before all even-positioned nodes, stop. This is the correct ordering.
- Then, rearrange the original linked list to match the ordering you found in the copied list.
Code Implementation
import itertools
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
def odd_even_linked_list_brute_force(head):
if not head:
return head
# Step 1: Copy the linked list to a list
node_list = []
current_node = head
while current_node:
node_list.append(current_node)
current_node = current_node.next
# Step 2: Generate all possible permutations of the list
for permutation in itertools.permutations(node_list):
# Step 3: Check if the current permutation satisfies the condition
is_valid = True
odd_indices = []
even_indices = []
for index, node in enumerate(permutation):
if (index + 1) % 2 != 0:
odd_indices.append(node)
else:
even_indices.append(node)
#Check if odds appear before evens
if len(even_indices) > 0 and len(odd_indices) > 0:
if node_list.index(odd_indices[-1]) > node_list.index(even_indices[0]):
is_valid = False
if is_valid:
#This satisfies the required condition
dummy_head = ListNode(0)
current = dummy_head
for node in permutation:
current.next = node
current = current.next
current.next = None #Terminate the list
#Step 5: Rearrange the original linked list
new_head = dummy_head.next
current_node = head
permutation_index = 0
while current_node:
current_node.val = permutation[permutation_index].val
current_node = current_node.next
permutation_index += 1
return head
return headBig(O) Analysis
Optimal Solution
Approach
The key is to separate the list into two smaller lists: one containing nodes in odd positions and one containing nodes in even positions. After constructing these two lists, link the end of the odd list to the beginning of the even list.
Here's how the algorithm would work step-by-step:
- Create two separate lists: one for the odd-positioned nodes and one for the even-positioned nodes.
- Traverse the original list, moving nodes from the original list to either the odd or even list based on their position.
- Keep track of the last node in the odd list.
- Once you've reached the end of the original list, connect the end of the odd list to the beginning of the even list.
- The head of the original list is now the head of the reordered list. Return this head.
Code Implementation
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
def oddEvenList(head):
if not head:
return head
odd_head = head
even_head = head.next
odd_pointer = odd_head
even_pointer = even_head
# Need to track end of odd list to connect later
last_odd_node = odd_head
while even_pointer and even_pointer.next:
odd_pointer.next = even_pointer.next
odd_pointer = odd_pointer.next
last_odd_node = odd_pointer
even_pointer.next = odd_pointer.next
even_pointer = even_pointer.next
# Connect odd list to the head of even list
last_odd_node.next = even_head
return odd_headBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty linked list (head is null) | Return null immediately as there are no nodes to reorder. |
| Single node linked list (head.next is null) | Return head directly, as there's only one (odd) node and nothing to reorder. |
| Two-node linked list (head.next.next is null) | Return head directly, as the first is odd, the second is even, and the structure is already correct. |
| Linked list with an even number of nodes | The loop condition must account for the fact that the last even node will point to null. |
| Linked list with an odd number of nodes | The loop condition must account for the fact that the last odd node will point to the next odd node after an even amount of nodes. |
| Very long linked list (potential memory issues) | The solution uses constant extra space, so it scales linearly with the input size and is unlikely to cause memory issues under reasonable size limits. |
| Linked list with cycles | The algorithm assumes a non-cyclic list; a cycle would lead to an infinite loop, so cycle detection should occur pre-processing, or use Floyd's cycle finding algorithm in tandem. |
| Integer overflow if node values are very large (not directly related to algorithm) | The algorithm does not directly manipulate the node values themselves, so integer overflow is not a relevant concern, but it may be needed to be considered in pre- or post- processing. |