Selling Pieces of Wood

Hard

Palantir

0 views

Topics:

Dynamic Programming

You are given two integers m and n that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array prices, where prices[i] = [h_i, w_i, price_i] indicates you can sell a rectangular piece of wood of height h_i and width w_i for price_i dollars.

To cut a piece of wood, you must make a vertical or horizontal cut across the entire height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to prices. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you cannot rotate a piece to swap its height and width.

Return the maximum money you can earn after cutting an m x n piece of wood.

Note that you can cut the piece of wood as many times as you want.

Example 1:

Input: m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]]
Output: 19
Explanation: The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 * 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 * 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 * 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.

Example 2:

Input: m = 4, n = 6, prices = [[3,2,10],[1,4,2],[4,1,3]]
Output: 32
Explanation: The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 * 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 * 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.

Constraints:

1 <= m, n <= 200
1 <= prices.length <= 2 * 10⁴
prices[i].length == 3
1 <= h_i <= m
1 <= w_i <= n
1 <= price_i <= 10⁶
All the shapes of wood (h_i, w_i) are pairwise distinct.

Selling Pieces of Wood

Hard

Palantir

0 views

Topics:

Dynamic Programming

You are given two integers m and n that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array prices, where prices[i] = [h_i, w_i, price_i] indicates you can sell a rectangular piece of wood of height h_i and width w_i for price_i dollars.

To cut a piece of wood, you must make a vertical or horizontal cut across the entire height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to prices. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you cannot rotate a piece to swap its height and width.

Return the maximum money you can earn after cutting an m x n piece of wood.

Note that you can cut the piece of wood as many times as you want.

Example 1:

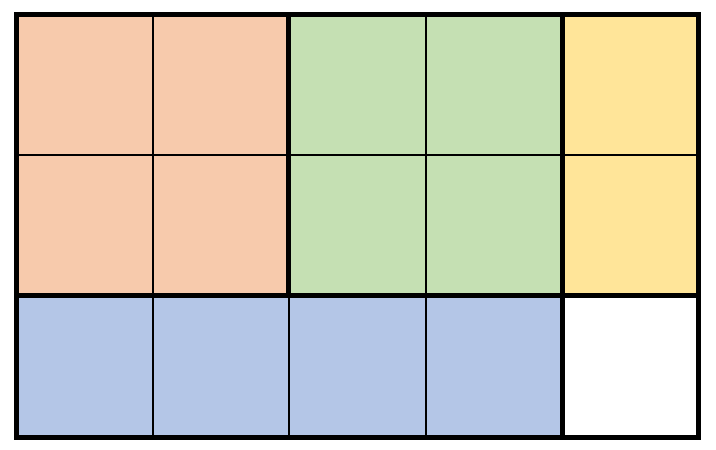
Input: m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]]
Output: 19
Explanation: The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 * 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 * 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 * 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.

Example 2:

Input: m = 4, n = 6, prices = [[3,2,10],[1,4,2],[4,1,3]]
Output: 32
Explanation: The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 * 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 * 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.

Constraints:

1 <= m, n <= 200
1 <= prices.length <= 2 * 10⁴
prices[i].length == 3
1 <= h_i <= m
1 <= w_i <= n
1 <= price_i <= 10⁶
All the shapes of wood (h_i, w_i) are pairwise distinct.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the dimensions `m` and `n` of the original wood piece, and on the height, width, and price values in the `prices` array?
If no combination of cuts and sales can generate any revenue, what should the function return (e.g., 0, -1, or null)?
Can the same piece of wood (same height and width) be sold multiple times if the `prices` array contains multiple entries with those dimensions?
Are `height_i` and `width_i` always smaller than or equal to `m` and `n`, respectively, or do I need to consider cases where the offered price is for a wood piece larger than the original?
Is the `prices` array guaranteed to be non-empty, or should I handle the case of an empty `prices` array?

Brute Force Solution

Approach

The brute force approach to selling wood involves trying every possible combination of cuts. We explore selling each possible piece that can be cut from the original wood and choose the combination that gives us the most money.

Here's how the algorithm would work step-by-step:

Consider all the different pieces of wood you can cut from the original piece.
For each piece, figure out how much money you would make if you sold it.
Try selling just one piece and calculate your total earnings.
Then, try selling two pieces, making sure they fit within the original piece of wood, and calculate your total earnings.
Continue trying all possible combinations of selling pieces, making sure each combination doesn't use more wood than you started with.
For each possible combination, calculate the total amount of money you would make.
Finally, compare the total earnings from all the different combinations and pick the one that gives you the most money.

Code Implementation

def selling_pieces_of_wood_brute_force(wood_length, prices):    max_profit = 0
    # Iterate through all possible combinations of cuts
    for i in range(1 << (wood_length - 1)):        current_length = 0
        current_profit = 0
        start_index = 0
        # Determine the cuts based on the binary representation
        for j in range(wood_length - 1):            if (i >> j) & 1:                piece_length = j - start_index + 1
                # Ensure that we don't exceed the wood length
                if piece_length <= wood_length:
                    if piece_length in prices:
                        current_profit += prices[piece_length]
                        current_length += piece_length
                        start_index = j + 1
                    else:
                        current_profit = -1
                        break
        # Handle the last piece of wood
        last_piece_length = wood_length - start_index
        if last_piece_length > 0:
            if last_piece_length in prices:
                current_profit += prices[last_piece_length]
                current_length += last_piece_length
            else:
                current_profit = -1

        #We only want to maximize profit if
        # the cuts are possible.
        if current_length <= wood_length and current_profit > max_profit:
            max_profit = current_profit
                return max_profit

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(2^n) – The algorithm considers all possible combinations of selling wood pieces. In the worst-case scenario, we have n possible wood pieces that can be cut. The total number of subsets (combinations) of these n pieces is 2^n, as each piece can either be included or excluded in a given combination. For each combination, we need to calculate the total earnings, taking O(n) time in the worst case because it might involve iterating through n different pieces to sum the amount of earning. Therefore, the time complexity will be proportional to 2^n * n. However, 2^n dominates n. Thus, the overall time complexity is O(2^n).

Space Complexity

O(2^N) – The brute force approach explores all possible combinations of cuts. The most significant space usage comes from storing these combinations. In the worst case, we might have to consider selling each piece individually, pairs of pieces, triplets, and so on, up to all possible pieces. If we consider 'N' as the potential number of pieces that could be cut and sold, then we are essentially considering all possible subsets of these 'N' pieces, resulting in the need to store up to 2^N combinations in the worst case. This leads to an auxiliary space proportional to the number of subsets, hence O(2^N).

Optimal Solution

Approach

The best way to solve this problem is to use a technique that breaks down the problem into smaller, solvable pieces. We can use a 'top-down' approach which makes use of precomputed answers and stores them for reuse. This avoids recalculating the same answers multiple times, resulting in a much faster solution.

Here's how the algorithm would work step-by-step:

Imagine you're starting with a large piece of wood and want to figure out the maximum profit you can make by cutting and selling smaller pieces.
Start by considering the simplest cases. For instance, what's the best profit you can get if you only have a tiny piece of wood? Store that answer.
Now, think about slightly larger pieces of wood. To figure out the best profit for a particular size, consider all the ways you could cut it. For each cut, figure out the profit you'd get from the piece you cut off, and add it to the best possible profit you could get from the remaining piece (which you've already calculated and stored!).
Choose the cutting strategy that gives you the highest total profit for that particular size of wood, and store that profit amount.
Keep doing this for increasingly larger pieces of wood. Each time, you're using the previously stored answers for smaller pieces to help you quickly figure out the best cutting strategy and profit for the current size.
Finally, when you reach the original size of the wood you started with, you'll have calculated and stored the absolute best profit you can possibly make, along with the cutting strategy to achieve it.

Code Implementation

def max_profit_wood_cutting(wood_length, wood_width, prices):
    # Initialize a table to store the maximum profit for each size.
    max_profit = [[0] * (wood_width + 1) for _ in range(wood_length + 1)]

    for current_length in range(1, wood_length + 1):
        for current_width in range(1, wood_width + 1):

            #Consider the price if we sell the current piece directly.
            max_profit[current_length][current_width] = prices.get((current_length, current_width), 0)

            # Iterate through all possible horizontal cuts.
            for horizontal_cut in range(1, current_length // 2 + 1):
                max_profit[current_length][current_width] = max(max_profit[current_length][current_width],
                                                max_profit[horizontal_cut][current_width] + max_profit[current_length - horizontal_cut][current_width])

            # Iterate through all possible vertical cuts.
            for vertical_cut in range(1, current_width // 2 + 1):
                max_profit[current_length][current_width] = max(max_profit[current_length][current_width],
                                                max_profit[current_length][vertical_cut] + max_profit[current_length][current_width - vertical_cut])

    # The bottom-right cell contains the max profit for the original size.
    return max_profit[wood_length][wood_width]

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n²) – The algorithm iterates through each possible wood size from 1 to n, where n is the initial size of the wood. For each size i, it considers all possible cut locations from 1 to i. This means that for each wood size, it performs a computation that is proportional to that size. Therefore, the total number of operations is roughly 1 + 2 + 3 + ... + n, which is the sum of an arithmetic series. This sum can be approximated as n * (n+1) / 2, which simplifies to O(n²).

Space Complexity

O(N) – The solution uses a top-down dynamic programming approach to store the maximum profit for each possible size of wood, from the smallest to the original size. This is done by storing the precomputed answers in a data structure. Specifically, an array (or similar data structure like a map or table) of size N is utilized, where N represents the original size of the wood. Therefore, the auxiliary space used is directly proportional to the size of the input, resulting in a space complexity of O(N).

Edge Cases

Case	How to Handle
m or n is zero	Return 0, as no wood exists to sell in this case.
prices is null or empty	Return 0, as no prices are provided to calculate the maximum value.
m and n are both 1, but no 1x1 piece is in prices	Return 0, as the available wood cannot be sold given the specified prices.
prices contain dimensions larger than m or n	Ignore price entries where height > m or width > n, as those cuts are not possible.
prices contain prices equal to zero.	The algorithm should still function correctly but these entries will have no impact on the maximum possible value.
Integer overflow possibility with very large m, n, or price values.	Use 64-bit integers (long) for intermediate calculations and final results to prevent overflow.
All prices are 0	The algorithm should correctly return 0 as the maximum profit in this scenario.
m and n are very large (e.g., 500), requiring significant DP table memory.	Ensure the solution's memory usage is optimized to avoid exceeding memory limits (consider bottom up DP if using recursion exceeds the stack limit).