Number of Valid Move Combinations On Chessboard

Hard

PayPal

0 views

Topics:

ArraysStringsRecursion

There is an 8 x 8 chessboard containing n pieces (rooks, queens, or bishops). You are given a string array pieces of length n, where pieces[i] describes the type (rook, queen, or bishop) of the i^th piece. In addition, you are given a 2D integer array positions also of length n, where positions[i] = [r_i, c_i] indicates that the i^th piece is currently at the 1-based coordinate (r_i, c_i) on the chessboard.

When making a move for a piece, you choose a destination square that the piece will travel toward and stop on.

A rook can only travel horizontally or vertically from (r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), or (r, c-1).
A queen can only travel horizontally, vertically, or diagonally from (r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), (r, c-1), (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).
A bishop can only travel diagonally from (r, c) to the direction of (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).

You must make a move for every piece on the board simultaneously. A move combination consists of all the moves performed on all the given pieces. Every second, each piece will instantaneously travel one square towards their destination if they are not already at it. All pieces start traveling at the 0^th second. A move combination is invalid if, at a given time, two or more pieces occupy the same square.

Return the number of valid move combinations.

Notes:

No two pieces will start in the same square.
You may choose the square a piece is already on as its destination.
If two pieces are directly adjacent to each other, it is valid for them to move past each other and swap positions in one second.

Example 1:

Input: pieces = ["rook"], positions = [[1,1]]
Output: 15
Explanation: The image above shows the possible squares the piece can move to.

Example 2:

Input: pieces = ["queen"], positions = [[1,1]]
Output: 22
Explanation: The image above shows the possible squares the piece can move to.

Example 3:

Input: pieces = ["bishop"], positions = [[4,3]]
Output: 12
Explanation: The image above shows the possible squares the piece can move to.

Constraints:

n == pieces.length
n == positions.length
1 <= n <= 4
pieces only contains the strings "rook", "queen", and "bishop".
There will be at most one queen on the chessboard.
1 <= r_i, c_i <= 8
Each positions[i] is distinct.

Number of Valid Move Combinations On Chessboard

Hard

PayPal

0 views

Topics:

ArraysStringsRecursion

There is an 8 x 8 chessboard containing n pieces (rooks, queens, or bishops). You are given a string array pieces of length n, where pieces[i] describes the type (rook, queen, or bishop) of the i^th piece. In addition, you are given a 2D integer array positions also of length n, where positions[i] = [r_i, c_i] indicates that the i^th piece is currently at the 1-based coordinate (r_i, c_i) on the chessboard.

When making a move for a piece, you choose a destination square that the piece will travel toward and stop on.

A rook can only travel horizontally or vertically from (r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), or (r, c-1).
A queen can only travel horizontally, vertically, or diagonally from (r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), (r, c-1), (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).
A bishop can only travel diagonally from (r, c) to the direction of (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).

You must make a move for every piece on the board simultaneously. A move combination consists of all the moves performed on all the given pieces. Every second, each piece will instantaneously travel one square towards their destination if they are not already at it. All pieces start traveling at the 0^th second. A move combination is invalid if, at a given time, two or more pieces occupy the same square.

Return the number of valid move combinations.

Notes:

No two pieces will start in the same square.
You may choose the square a piece is already on as its destination.
If two pieces are directly adjacent to each other, it is valid for them to move past each other and swap positions in one second.

Example 1:

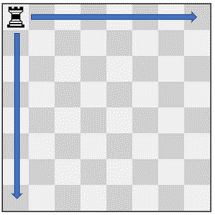
Input: pieces = ["rook"], positions = [[1,1]]
Output: 15
Explanation: The image above shows the possible squares the piece can move to.

Example 2:

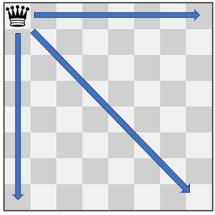
Input: pieces = ["queen"], positions = [[1,1]]
Output: 22
Explanation: The image above shows the possible squares the piece can move to.

Example 3:

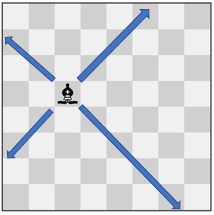
Input: pieces = ["bishop"], positions = [[4,3]]
Output: 12
Explanation: The image above shows the possible squares the piece can move to.

Constraints:

n == pieces.length
n == positions.length
1 <= n <= 4
pieces only contains the strings "rook", "queen", and "bishop".
There will be at most one queen on the chessboard.
1 <= r_i, c_i <= 8
Each positions[i] is distinct.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the maximum values for 'n' (chessboard size), the number of pieces, and the length of each move sequence?
Can a piece stay in the same cell for multiple moves in its sequence, and if so, is that still considered a valid move?
If no valid combinations exist, what should the function return (e.g., 0, -1, null)?
Are the initial positions of the pieces guaranteed to be unique, or can multiple pieces start in the same cell?
Are the moves in a move sequence relative (e.g., 'up', 'down', 'left', 'right') or absolute coordinates on the board?

Brute Force Solution

Approach

The core idea is to explore every possible sequence of moves for each piece. We will simulate all combinations of moves until a solution is found or all possibilities are exhausted. It's like trying every combination lock until you find the correct one.

Here's how the algorithm would work step-by-step:

Consider each piece on the chessboard one by one.
For each piece, determine all possible single moves it can make based on the chessboard rules.
Combine these single moves to form sequences of moves for each piece.
Try out all possible combinations of move sequences for all the pieces.
For each complete combination of move sequences, check if the combination is valid by ensuring pieces do not collide or end up in the same spot at the same time.
If a combination is valid, increment the count of valid combinations.
Repeat this process until all possible combinations of move sequences have been explored.
The total count of valid combinations found is the answer.

Code Implementation

def find_valid_move_combinations_brute_force(pieces, board_size):
    number_of_pieces = len(pieces)
    valid_combinations_count = 0

    def is_valid_move(move):
        # Placeholder: Replace with actual move validation logic
        # For simplicity, always return True
        return True

    def is_valid_combination(moves):
        # Placeholder: Replace with actual combination validation logic
        # For simplicity, always return True
        return True

    def generate_moves(current_piece_index, current_moves):
        nonlocal valid_combinations_count

        # If all pieces have moved, check if the combination is valid.
        if current_piece_index == number_of_pieces:
            if is_valid_combination(current_moves):
                valid_combinations_count += 1
            return

        piece = pieces[current_piece_index]

        # Iterate through possible moves for the current piece.
        for row in range(board_size):
            for col in range(board_size):
                move = (piece, (row, col))

                # Check if the current move is valid.
                if is_valid_move(move):
                    generate_moves(current_piece_index + 1, current_moves + [move])

    # Start the recursive move generation from the first piece.
    generate_moves(0, [])

    return valid_combinations_count

Big(O) Analysis

Time Complexity

O(M^P) – Let M be the maximum number of possible moves a single piece can make. Let P be the number of pieces on the board. The algorithm explores all possible move sequences for each piece. In the worst case, each piece could have M possible moves. The algorithm needs to check every combination of these move sequences for all P pieces, resulting in roughly M multiplied by itself P times, which is M^P. Therefore, the time complexity is O(M^P).

Space Complexity

O(M * L) – The space complexity is dominated by storing the possible move sequences for each piece. Let M be the maximum number of moves a single piece can make, and L be the number of pieces. For each piece, we may need to store a list of possible move sequences, each of length up to M. The algorithm also explores combinations of these move sequences, implicitly storing intermediate states in the form of lists of moves for each piece, which at worst can be of size proportional to M per piece for all L pieces. Therefore, auxiliary space to store the possible move combinations is O(M * L). Temporary variables for checking collisions contribute O(1) space.

Optimal Solution

Approach

The problem involves figuring out how chess pieces can move without blocking each other. The optimal approach is to view the chessboard and pieces as a graph and uses graph traversal to systematically explore possible move combinations. This avoids redundant calculations, significantly speeding up the process.

Here's how the algorithm would work step-by-step:

Represent the chessboard as a graph where each square is a point and possible moves between squares are connections.
Consider each chess piece and how it can move based on the type of piece.
Try all possible paths for the first piece, marking which squares are occupied as the piece moves.
For each path of the first piece, try all possible paths for the second piece, keeping in mind squares now blocked by the first piece.
Continue this process for each chess piece. If a piece can't move without collision on the board or another piece, that branch of possibilities is abandoned.
Keep track of successful combinations that don't have any collisions.
Finally, count all of these valid combinations to get the answer.

Code Implementation

def number_of_valid_move_combinations_on_chessboard(piece_positions, piece_moves):
    number_of_pieces = len(piece_positions)
    adjacency_list = [[] for _ in range(number_of_pieces)]

    for first_piece_index in range(number_of_pieces):
        for second_piece_index in range(first_piece_index + 1, number_of_pieces):
            adjacency_list[first_piece_index].append(second_piece_index)
            adjacency_list[second_piece_index].append(first_piece_index)

    number_of_moves = [len(moves) for moves in piece_moves]
    total_move_combinations = 1
    for move_count in number_of_moves:
        total_move_combinations *= move_count

    move_combinations_count = 0

    #Use a cache to avoid duplicate work
    cache = {}

    def depth_first_search(piece_index, current_moves):
        nonlocal move_combinations_count

        if piece_index == number_of_pieces:
            move_combinations_count += 1
            return

        cache_key = tuple(current_moves)
        if cache_key in cache:
            move_combinations_count += cache[cache_key]
            return

        valid_combinations_from_here = 0

        for move_index in range(number_of_moves[piece_index]):
            is_valid_move = True
            for previous_piece_index in range(piece_index):
                #Check for collision with previous moves
                if (current_moves[previous_piece_index] == move_index and
                        adjacency_list[piece_index] and previous_piece_index in adjacency_list[piece_index]):
                    is_valid_move = False
                    break

            if is_valid_move:
                current_moves[piece_index] = move_index
                depth_first_search(piece_index + 1, current_moves)

        cache[cache_key] = valid_combinations_from_here

    # Start the depth first search exploration
    depth_first_search(0, [0] * number_of_pieces)

    # Return the number of valid combinations found
    return move_combinations_count

Big(O) Analysis

Time Complexity

O(P^N) – The algorithm explores all possible move combinations for N chess pieces on a chessboard where each piece potentially has P possible paths. For each piece, the algorithm considers all its possible moves, leading to an exponential branching factor. Since each piece can potentially have multiple valid paths and these paths are explored in combination with paths of all other pieces, the total number of combinations grows exponentially with the number of pieces. Therefore, the time complexity is approximately O(P^N), where P is the maximum number of paths a single piece can take and N is the number of pieces.

Space Complexity

O(K * M) – The space complexity is primarily determined by the graph traversal and path exploration for each piece. The algorithm stores occupied squares during the path exploration, which could involve storing the paths for all K pieces. For each piece, the longest possible path is limited by the maximum moves a piece can make which in a chessboard can be bound to some constant M. Therefore, we need to store information for K pieces, where for each piece, at worst, a path of M squares is stored. The auxiliary space approximates to K * M, and in Big O notation, this is O(K * M), where K is the number of pieces and M is the maximum number of moves a piece can make.

Edge Cases

Case	How to Handle
Null or empty positions array	Return 1, indicating one valid combination (doing nothing).
Null or empty move sequences array	Return 1, indicating one valid combination (doing nothing for that piece).
Chessboard size of 1x1	Check for immediate collisions if any moves are made.
Single piece on the board	Return the number of valid move sequences for that piece.
Maximum board size and maximum number of pieces to test scalability.	Optimize the collision detection to avoid excessive time complexity with a large board.
Pieces starting in the same location	The algorithm must account for immediate collisions if pieces start on the same square.
Move sequences that result in the pieces leaving the board.	Treat out-of-bounds moves as invalid and reject that particular move sequence.
Very long move sequences for some or all pieces.	Consider memory limits during recursive or iterative processing of move sequences to prevent stack overflow or OOM errors.