Maximum Profit in Job Scheduling

Hard

2 views

Topics:

Dynamic ProgrammingBinary Search

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

1 <= startTime.length == endTime.length == profit.length <= 5 * 10⁴
1 <= startTime[i] < endTime[i] <= 10⁹
1 <= profit[i] <= 10⁴

Maximum Profit in Job Scheduling

Hard

2 views

Topics:

Dynamic ProgrammingBinary Search

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

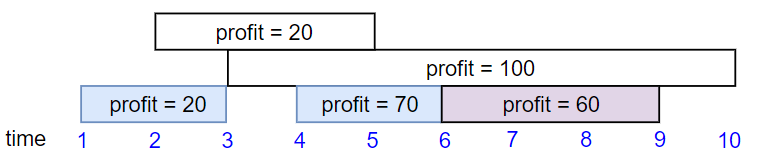
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

1 <= startTime.length == endTime.length == profit.length <= 5 * 10⁴
1 <= startTime[i] < endTime[i] <= 10⁹
1 <= profit[i] <= 10⁴

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the size of the `startTime`, `endTime`, and `profit` arrays, and what is the range of values for the start times, end times and profits?
Can jobs have the same start and end times (i.e., zero duration)? If so, are they still valid jobs that can contribute to the profit?
If no jobs can be scheduled without overlap, what value should I return?
Are the `startTime`, `endTime`, and `profit` arrays guaranteed to have the same length? What should I do if they don't?
Can the start and end times overlap *exactly* (e.g., job A ends at 5 and job B starts at 5)? If so, are these considered overlapping and not allowed to be scheduled together?

Brute Force Solution

Approach

The brute force method to maximize profit from job scheduling is like trying out every possible combination of jobs. We explore all potential schedules, calculating the profit for each, and then pick the schedule that gives us the biggest reward. It's an exhaustive search through all options.

Here's how the algorithm would work step-by-step:

Consider each job one at a time. For each job, you have two choices: either include it in your schedule or don't include it.
If you choose to include a job, you have to make sure it doesn't overlap with any other jobs already in your schedule. If it does, you can't include it.
Keep track of the profit you get for each possible combination of jobs.
After you've explored all possible combinations of including and excluding jobs, compare the profits of all the valid schedules you found.
The schedule with the highest profit is the solution.

Code Implementation

def max_profit_job_scheduling_brute_force(start_times, end_times, profits):
    number_of_jobs = len(start_times)

    def calculate_max_profit(current_index, current_schedule_end_time):
        # If we've reached the end of the jobs, return 0
        if current_index == number_of_jobs:
            return 0

        # Option 1: Exclude the current job
        profit_excluding_current_job = calculate_max_profit(
            current_index + 1,
            current_schedule_end_time
        )

        # Option 2: Include the current job if it doesn't overlap
        profit_including_current_job = 0
        if start_times[current_index] >= current_schedule_end_time:
            # Only include if no overlap, check constraint
            profit_including_current_job = profits[current_index] + \
                calculate_max_profit(
                    current_index + 1,
                    end_times[current_index]
                )

        # Return the maximum of the two options
        return max(
            profit_excluding_current_job,
            profit_including_current_job
        )

    # Start the recursion with the first job and no jobs scheduled
    return calculate_max_profit(0, 0)

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(2^n) – The brute force approach considers each job and makes a binary choice: either include it in the schedule or exclude it. With n jobs, this creates a decision tree where each level corresponds to a job, and each node has two branches (include or exclude). Therefore, there are 2^n possible paths or schedules to explore. Calculating the profit for each schedule involves checking for overlaps, but the dominant factor is the exploration of all 2^n subsets of jobs, leading to an overall time complexity of O(2^n).

Space Complexity

–

Optimal Solution

Approach

The optimal approach for job scheduling maximizes profit by intelligently selecting compatible jobs. It involves sorting the jobs and using a technique to avoid re-calculating the maximum profit for overlapping scenarios, leading to significant efficiency gains.

Here's how the algorithm would work step-by-step:

First, organize the jobs by their finish times from earliest to latest.
Then, go through the jobs in this order, figuring out the maximum profit we can make up to each job.
For each job, we have two choices: either take it or leave it. If we leave it, the best profit we can make is the same as the best profit we had before considering this job.
If we take the job, we also need to find the latest job that finishes before the current job starts (because we can't do overlapping jobs).
Once we find that previous compatible job, the best profit we can make by taking the current job is the sum of its profit and the best profit we could make up to that previous compatible job.
Compare the profit from taking the job with the profit from not taking the job, and choose the bigger one. This is the maximum profit we can make up to the current job.
Store the maximum profit for each job in a way that we can easily look it up later, avoiding recalculating the same thing multiple times.
Continue this process for all jobs, and the final maximum profit we calculated will be the overall maximum profit possible.

Code Implementation

def job_scheduling(start_time, end_time, profit):
    jobs = sorted(zip(start_time, end_time, profit), key=lambda x: x[1])
    number_of_jobs = len(jobs)
    dp_table = [0] * number_of_jobs

    dp_table[0] = jobs[0][2]

    for i in range(1, number_of_jobs):
        # Include current job's profit.
        current_profit = jobs[i][2]
        
        # Find compatible job using binary search
        left = 0
        right = i - 1
        last_compatible_job_index = -1

        while left <= right:
            mid = (left + right) // 2
            if jobs[mid][1] <= jobs[i][0]:
                last_compatible_job_index = mid
                left = mid + 1
            else:
                right = mid - 1

        # Add profit from compatible job
        if last_compatible_job_index != -1:
            current_profit += dp_table[last_compatible_job_index]

        # Choose max profit between including/excluding
        dp_table[i] = max(current_profit, dp_table[i-1])

        # Store max profit up to ith job

    return dp_table[number_of_jobs - 1]

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n log n) – The dominant operations contributing to the time complexity are sorting the jobs initially, which takes O(n log n) time, and the binary search performed within the loop to find the latest non-overlapping job. The main loop iterates through the n jobs, and inside the loop, binary search takes O(log n) time. Therefore, the overall time complexity is O(n log n) + O(n log n), which simplifies to O(n log n).

Space Complexity

O(N) – The solution uses dynamic programming to store the maximum profit achievable up to each job. This requires an auxiliary array (or similar data structure, depending on implementation) to store these intermediate maximum profit values. Since we calculate and store the maximum profit for each of the N jobs, the space used by this array grows linearly with the number of jobs, N. Therefore, the auxiliary space complexity is O(N).

Edge Cases

Case	How to Handle
Empty input arrays (startTime, endTime, profit)	Return 0 as there are no jobs to schedule.
Single job available (array size is 1)	Return the profit of the single job.
All jobs overlap with each other (e.g., same start and end times)	The algorithm should correctly identify that only one job can be selected, and choose the one with maximum profit.
Jobs with zero profit	The algorithm should handle zero profit jobs correctly; including or excluding them based on whether they maximize overall profit.
Jobs with very large start/end times leading to potential integer overflow	Use 64-bit integers (long in Java/C++) to prevent overflow during calculations like binary search or dynamic programming table indexing if applicable.
startTime and endTime arrays are not sorted correctly	Sort the jobs based on their end times to facilitate the dynamic programming approach for finding non-overlapping jobs.
Large input size: startTime, endTime, profit arrays with n = 5 * 10^4	Ensure the algorithm uses an efficient sorting algorithm (O(n log n)) and a dynamic programming approach to achieve an acceptable time complexity.
Duplicate jobs with identical startTime, endTime, and profit	The algorithm should treat them as distinct jobs if allowed or aggregate profits if the constraints explicitly disallow duplicates.