All Ancestors of a Node in a Directed Acyclic Graph

Medium

Asked by:

52 views

Topics:

GraphsDynamic Programming

You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive).

You are also given a 2D integer array edges, where edges[i] = [from_i, to_i] denotes that there is a unidirectional edge from from_i to to_i in the graph.

Return a list answer, where answer[i] is the list of ancestors of the i^th node, sorted in ascending order.

A node u is an ancestor of another node v if u can reach v via a set of edges.

Example 1:

Input: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
Output: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.

Example 2:

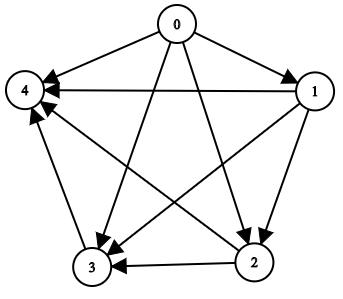
Input: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Output: [[],[0],[0,1],[0,1,2],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.

Constraints:

1 <= n <= 1000
0 <= edges.length <= min(2000, n * (n - 1) / 2)
edges[i].length == 2
0 <= from_i, to_i <= n - 1
from_i != to_i
There are no duplicate edges.
The graph is directed and acyclic.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the maximum number of nodes (n) and edges (m) that the graph can have? This will help me understand potential memory and time complexity constraints.
Are the node values represented by integers, and if so, what is the range of possible integer values for the nodes?
If a node has no ancestors, should I return an empty list for that node, or is there another specified default value/behavior?
Is the input graph guaranteed to be a valid Directed Acyclic Graph (DAG), or do I need to handle cases where cycles might exist?
For each node, are the ancestors in the returned list expected to be in any specific order (e.g., topological order, ascending order of node value)?

Brute Force Solution

Approach

To find all ancestors of a specific node, we can explore every possible path in the graph. We essentially walk backwards from the target node, tracking every node we encounter along the way. If we ever revisit a node, we know it is an ancestor.

Here's how the algorithm would work step-by-step:

Start at the node you're interested in.
Look at all the nodes that directly point to it.
For each of those nodes, consider them a possible ancestor and add them to your list.
Now, for each of those possible ancestors, look at all the nodes that point to them.
Add these new nodes to your list of possible ancestors.
Keep repeating this process of finding nodes that point to the nodes you've already found.
If you encounter the same node multiple times, it's still only listed once as an ancestor.
Stop when you have explored all possible paths backwards from the starting node, or when you reach a node with no incoming connections.
The final list of unique nodes you found are all the ancestors of the original node.

Code Implementation

def all_ancestors_brute_force(number_of_nodes, edges, target_node):

    ancestors = set()
    queue = [target_node]

    while queue:
        current_node = queue.pop(0)

        for possible_ancestor in range(number_of_nodes):
            # Check each node to see if it points to the current node.
            if (possible_ancestor, current_node) in edges:
                # Ensure ancestor is only added once.
                if possible_ancestor not in ancestors:

                    ancestors.add(possible_ancestor)
                    # Add the possible ancestor to the queue to explore its ancestors.
                    queue.append(possible_ancestor)

    return sorted(list(ancestors))

Big(O) Analysis

Time Complexity

O(n + e) – The algorithm essentially performs a Depth First Search (DFS) or Breadth First Search (BFS) traversal of the graph, starting from the target node and traversing backward along the edges. In the worst case, it visits every node (n) and every edge (e) in the graph, in the reverse direction of the original edges, once. Therefore, the time complexity is determined by the number of nodes and edges visited during the traversal. The algorithm will visit the edges (e) and nodes (n). As such the runtime is O(n + e).

Space Complexity

O(N) – The algorithm uses a list (or set) to store possible ancestors and this list grows as we explore backwards from the target node. In the worst case, where every node is an ancestor of the target node, the list of ancestors could contain all nodes in the graph. The algorithm also implicitly uses a queue (or stack) in a breadth-first (or depth-first) search fashion to explore all possible paths, potentially storing up to N nodes at any time, where N is the number of nodes in the graph. Therefore, the auxiliary space complexity is O(N).

Optimal Solution

Approach

To efficiently find all ancestors of each node in a directed acyclic graph, we'll perform a traversal from each node upwards. We avoid redundant work by remembering the ancestors we've already found for each node, storing that information to be reused later.

Here's how the algorithm would work step-by-step:

For each node in the graph, we want to find all of its ancestors.
Start with a given node. Use a way to explore the graph upwards, such as by going to a node's parents.
As you find an ancestor of the starting node, record it.
Crucially, remember the ancestors you find for each node. If you visit a node again during the traversal, you can immediately use the stored information instead of recomputing it.
Repeat this process for every node in the graph to ensure you've found all ancestors for each one.
Finally, organize the ancestors for each node in an organized way, for example, in increasing order.

Code Implementation

def all_ancestors_of_a_node_in_dag(number_of_nodes, edges):
    graph = [[] for _ in range(number_of_nodes)]
    for start_node, end_node in edges:
        graph[start_node].append(end_node)

    all_ancestors = [set() for _ in range(number_of_nodes)]

    def depth_first_search(node, current_ancestors):
        # If we've already computed the ancestors, reuse them.
        if all_ancestors[node]:
            return all_ancestors[node]

        ancestors = set(current_ancestors)

        # Traverse the graph to find ancestors.
        for neighbor in graph[node]:
            neighbor_ancestors = depth_first_search(neighbor, current_ancestors | {neighbor})
            ancestors.update(neighbor_ancestors)

        all_ancestors[node] = ancestors
        return ancestors

    # Perform a DFS from each node.
    for node in range(number_of_nodes):
        depth_first_search(node, {node})

    result = [sorted(list(ancestors)) for ancestors in all_ancestors]
    return result

Big(O) Analysis

Time Complexity

O(n*m) – We iterate through each of the 'n' nodes in the graph to find their ancestors. For each node, we perform a traversal upwards through the graph, visiting its parents and their ancestors. In the worst case, for a single node, we might traverse all 'm' edges in the graph (where 'm' represents the number of edges). Remembering previously computed ancestors prevents redundant traversal within a single node's ancestor search. Therefore, the overall time complexity is O(n*m), reflecting the potential for traversing all edges for each node.

Space Complexity

O(N^2) – The algorithm stores ancestors for each node to avoid redundant calculations. In the worst-case scenario, each node could potentially be an ancestor of every other node. This leads to an auxiliary data structure (e.g., a dictionary or list of lists) storing, for each of the N nodes, a list of its ancestors, which could also be up to N in size. Therefore, the space required to store the ancestors for all nodes could grow up to N * N = N^2. The algorithm also employs a queue or stack for traversal, but the size of the queue/stack is at most N, which is dominated by the N^2 space complexity of the ancestor storage.

Edge Cases

Case	How to Handle
Null or empty graph (no nodes or edges)	Return an empty list for each node in the result since there are no ancestors.
Single node graph (only one node, no edges)	The single node has no ancestors, so return an empty list for it.
Graph with a single edge (e.g., 0 -> 1)	Node 1's ancestor is 0, and node 0 has no ancestors; handle correctly during traversal.
Node with no ancestors (root node(s))	The result for such nodes will be an empty list as no ancestor exists to add.
Graph where all nodes are ancestors of a single node.	The algorithm will correctly identify all other nodes as ancestors of the final node.
Large graph to check for efficient memory usage and time complexity	Use an efficient traversal algorithm (e.g., DFS or BFS with appropriate data structures) to avoid excessive memory consumption and prevent timeouts.
Graph represented with a very large number of nodes, potentially nearing integer limits	Ensure node IDs are stored as data types capable of representing the entire range (e.g., long in Java/C++) to prevent overflow issues.
Disconnected graph components	The algorithm should handle disconnected components by correctly identifying ancestors within each component, returning empty lists for nodes in other components when traversing from a specific node.

Null or empty graph (no nodes or edges)

How to Handle:

Return an empty list for each node in the result since there are no ancestors.

Single node graph (only one node, no edges)

How to Handle:

The single node has no ancestors, so return an empty list for it.

Graph with a single edge (e.g., 0 -> 1)

How to Handle:

Node 1's ancestor is 0, and node 0 has no ancestors; handle correctly during traversal.

Node with no ancestors (root node(s))

How to Handle:

The result for such nodes will be an empty list as no ancestor exists to add.

Graph where all nodes are ancestors of a single node.

How to Handle:

The algorithm will correctly identify all other nodes as ancestors of the final node.

Large graph to check for efficient memory usage and time complexity

How to Handle:

Use an efficient traversal algorithm (e.g., DFS or BFS with appropriate data structures) to avoid excessive memory consumption and prevent timeouts.

Graph represented with a very large number of nodes, potentially nearing integer limits

How to Handle:

Ensure node IDs are stored as data types capable of representing the entire range (e.g., long in Java/C++) to prevent overflow issues.

Disconnected graph components

How to Handle:

The algorithm should handle disconnected components by correctly identifying ancestors within each component, returning empty lists for nodes in other components when traversing from a specific node.