All Paths From Source to Target
MediumGiven a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.
The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).
Example 1:
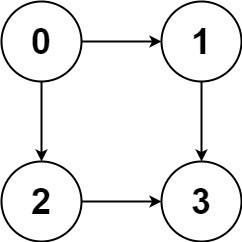
Input: graph = [[1,2],[3],[3],[]] Output: [[0,1,3],[0,2,3]] Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
Example 2:
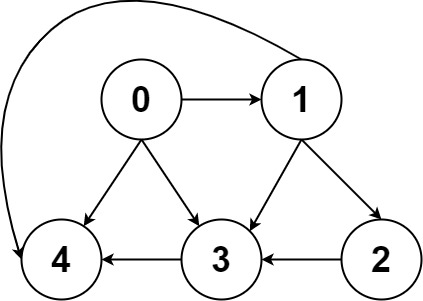
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]] Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
Constraints:
n == graph.length2 <= n <= 150 <= graph[i][j] < ngraph[i][j] != i(i.e., there will be no self-loops).- All the elements of
graph[i]are unique. - The input graph is guaranteed to be a DAG.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Is the graph represented as an adjacency list or an adjacency matrix, and what are the data types for the nodes and edges?
- Are cycles allowed in the graph, and if so, should the paths avoid cycles?
- What is the expected format of the output? Should the paths be ordered, and if so, how?
- What should I return if there is no path from the source to the target node?
- Are the node values guaranteed to be within a specific range, and what is the maximum number of nodes I should expect?
Brute Force Solution
Approach
The brute force method for finding all paths involves exploring every possible route from the starting point to the destination. We essentially try out every single possible path, one by one, to see if it leads to the target. It's like trying every door in a maze until you find the exit.
Here's how the algorithm would work step-by-step:
- Begin at the starting point.
- Explore every possible path extending from the current location.
- For each path, continue exploring all possible extensions until either the destination is reached or the path becomes invalid (e.g., leads to a dead end or a previously visited place).
- If a path reaches the destination, record it as a valid solution.
- Repeat this process for every starting direction and path until all possible routes have been explored.
- The result is a collection of all the paths that successfully lead from the source to the target.
Code Implementation
def all_paths_source_target(graph):
target_node = len(graph) - 1
all_possible_paths = []
def find_all_paths(current_node, current_path):
# Append the current node to the current path
current_path = current_path + [current_node]
# If we've reached the target, save the path
if current_node == target_node:
all_possible_paths.append(current_path)
return
# If there are no outgoing edges, stop
if not graph[current_node]:
return
# Iterate through the neighbors of current node
for neighbor_node in graph[current_node]:
# Recursively call to explore paths
find_all_paths(neighbor_node, current_path)
find_all_paths(0, [])
return all_possible_pathsBig(O) Analysis
Optimal Solution
Approach
The best way to find all possible paths is to explore each path one step at a time. We'll use a method that remembers where we've been and branches out to try every possible next step until we reach our destination, or a dead end.
Here's how the algorithm would work step-by-step:
- Start at the beginning.
- From where you are, look at all the possible places you can go next.
- For each of those possible places, imagine taking that step and adding it to your current path.
- If a path leads to the final destination, save it.
- If a path leads to a place where you can't go any further, abandon it.
- Repeat the process of exploring from each new place until all possibilities are exhausted.
- The saved paths are all the possible routes from beginning to end.
Code Implementation
def all_paths_source_target(graph):
target_node = len(graph) - 1
all_possible_paths = []
def find_all_paths(current_node, current_path):
# Append the current node to the current path.
current_path.append(current_node)
# If we've reached the target, save the path.
if current_node == target_node:
all_possible_paths.append(current_path.copy())
else:
# Explore all possible next nodes from the current node.
for next_node in graph[current_node]:
find_all_paths(next_node, current_path)
# Backtrack: Remove the current node to explore other paths.
current_path.pop()
# Start the search from the source node (0).
find_all_paths(0, [])
return all_possible_pathsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty graph input | Return an empty list, as there are no paths in an empty graph. |
| Graph with a single node (source is target) | Return a list containing a single path with only the source node. |
| Graph with no paths from source to target | Return an empty list, indicating no path exists. |
| Graph with cycles (directed acyclic graph violation) | The algorithm should still work correctly by exploring all possible paths, but may take longer due to revisiting nodes; cycle detection is unnecessary given problem constraints. |
| Graph with multiple paths from source to target | The algorithm must return all possible paths, not just one. |
| Large graph, potential stack overflow with recursion | Consider iterative deepening depth-first search to avoid stack overflow if recursion depth becomes too large. |
| Graph with a single path, extremely long path | Ensure that the solution does not exceed memory limits due to a very long path being stored. |
| Source or target node does not exist | While the problem states the source is 0 and target is N-1, a check could be implemented for robustness to ensure both are within graph bounds and throw an exception or return an empty list if not. |