All Possible Full Binary Trees #8 Most Asked
MediumGiven an integer n, return a list of all possible full binary trees with n nodes. Each node of each tree in the answer must have Node.val == 0.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in any order.
A full binary tree is a binary tree where each node has exactly 0 or 2 children.
Example 1:
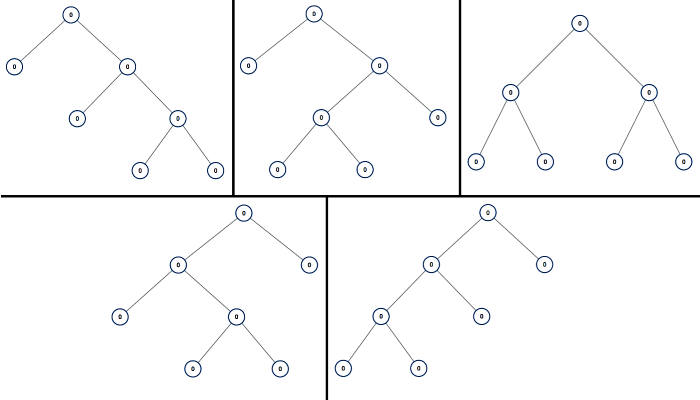
Input: n = 7 Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
Example 2:
Input: n = 3 Output: [[0,0,0]]
Constraints:
1 <= n <= 20
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of possible values for `n`?
- Is `n` guaranteed to be an odd number, since a full binary tree must have an odd number of nodes?
- If `n` is an even number, should I return an empty list or is there some other expected behavior?
- Is the order of the trees in the output list important?
- Should I return the actual TreeNode objects or some serialized representation of them?
Brute Force Solution
Approach
The brute force approach to building all full binary trees involves generating every possible tree structure for a given number of nodes. We explore each possibility, one by one, until we have covered all the valid combinations. Each tree is built and checked to see if it fits the requirements.
Here's how the algorithm would work step-by-step:
- Start by considering a single node as the root of the tree.
- Then, for each node count, explore every possible split into left and right subtrees.
- For each split, recursively build all possible left subtrees and all possible right subtrees.
- Combine each left subtree with each right subtree to form a new full binary tree.
- Check if the resulting tree has the correct total number of nodes and if it meets the 'full' binary tree requirement, meaning each node has either 0 or 2 children.
- If it is a valid full binary tree, add it to the collection of possible trees.
- Repeat this process until all combinations of subtrees have been explored for the given number of nodes.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
def all_possible_fbt(number_of_nodes):
# Base case: if number_of_nodes is even, no full binary tree exists
if number_of_nodes % 2 == 0:
return []
# Base case: if number_of_nodes is 1, the only full binary tree is a single node
if number_of_nodes == 1:
return [TreeNode()]
result = []
# Iterate through all possible combinations of left and right subtrees
for left_subtree_size in range(1, number_of_nodes, 2):
right_subtree_size = number_of_nodes - 1 - left_subtree_size
# Recursively generate all possible left subtrees
all_left_subtrees = all_possible_fbt(left_subtree_size)
# Recursively generate all possible right subtrees
all_right_subtrees = all_possible_fbt(right_subtree_size)
# Combine each left subtree with each right subtree to form a new tree
for left_subtree in all_left_subtrees:
for right_subtree in all_right_subtrees:
root = TreeNode()
root.left = left_subtree
root.right = right_subtree
result.append(root)
return resultBig(O) Analysis
Optimal Solution
Approach
The key idea is to build full binary trees recursively. We realize that any full binary tree can be broken down into a root node, a left subtree, and a right subtree, both of which must also be full binary trees.
Here's how the algorithm would work step-by-step:
- If we want to build a full binary tree with a certain number of nodes, that number must be odd. If it's even, we can't build one, so we return nothing.
- We know that any full binary tree has a root node. So, we need to figure out how many nodes go into the left and right subtrees.
- We can try all possible combinations of left and right subtree sizes that add up to the total number of nodes minus one (for the root). For example, if we have 7 nodes, we can try a left subtree of size 1 and a right subtree of size 5, or a left subtree of size 3 and a right subtree of size 3, and so on.
- For each combination of left and right subtree sizes, recursively build the left and right subtrees. This gives us a collection of left subtrees and right subtrees.
- Take each possible left subtree and combine it with each possible right subtree to form a new full binary tree, with a new root node connecting them.
- Keep building all possible trees in this fashion and eventually return every single possibility to the initial caller.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def allPossibleFBT(self, number_of_nodes: int) -> list[TreeNode]:
# Only odd numbers can form a full binary tree
if number_of_nodes % 2 == 0:
return []
if number_of_nodes == 1:
return [TreeNode()]
result = []
# Iterate through possible sizes of the left subtree
for left_subtree_size in range(1, number_of_nodes, 2):
right_subtree_size = number_of_nodes - 1 - left_subtree_size
# Recursively generate all possible left subtrees
all_possible_left_subtrees = self.allPossibleFBT(left_subtree_size)
# Recursively generate all possible right subtrees
all_possible_right_subtrees = self.allPossibleFBT(right_subtree_size)
# Combine each left and right subtree to form a new tree
for left_subtree in all_possible_left_subtrees:
for right_subtree in all_possible_right_subtrees:
root = TreeNode()
root.left = left_subtree
root.right = right_subtree
result.append(root)
return resultBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| n is 0 | Return an empty list as there are no possible full binary trees with 0 nodes. |
| n is an even number | Return an empty list since a full binary tree must have an odd number of nodes. |
| n is 1 | Return a list containing a single tree with one node. |
| n is a large odd number, potentially causing excessive recursion | Employ memoization to store already computed full binary trees for subproblems to improve efficiency. |
| Integer overflow during node creation if n is extremely large. | Check for potential integer overflows when creating nodes and handle appropriately, potentially using larger data types. |
| Memory exhaustion with very large n due to the exponential growth of possible trees | Consider a limit on the maximum value of n, or streaming results to avoid storing all trees simultaneously. |
| Repeated calls to the function with the same n value. | Use memoization to store results of previous calls and return cached result for subsequent calls with same n. |
| n is a negative number. | Treat as invalid input and throw an IllegalArgumentException, or return an empty list. |