Allocate Mailboxes
HardGiven the array houses where houses[i] is the location of the ith house along a street and an integer k, allocate k mailboxes in the street.
Return the minimum total distance between each house and its nearest mailbox.
The test cases are generated so that the answer fits in a 32-bit integer.
Example 1:
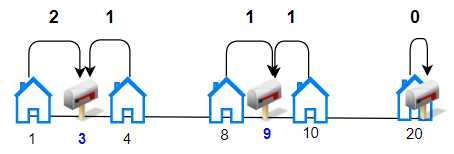
Input: houses = [1,4,8,10,20], k = 3 Output: 5 Explanation: Allocate mailboxes in position 3, 9 and 20. Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
Example 2:

Input: houses = [2,3,5,12,18], k = 2 Output: 9 Explanation: Allocate mailboxes in position 3 and 14. Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
Constraints:
1 <= k <= houses.length <= 1001 <= houses[i] <= 104- All the integers of
housesare unique.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of possible values for the mailbox locations (house positions)? Can they be negative, zero, or very large?
- How many mailboxes (k) will we need to allocate, and what is the relationship between k and the number of houses? Can k ever be 0, 1, or greater than the number of houses?
- If there are multiple equally optimal placements of mailboxes (resulting in the same minimum total distance), is any one of those placements acceptable, or is there a specific criteria for choosing amongst them?
- What data type should I use to represent the total distance? Should I anticipate potential integer overflow issues?
- What should I return if the input array of house locations is null or empty, or if k is invalid (e.g., k <= 0)?
Brute Force Solution
Approach
The brute force approach to the mailbox problem means trying every possible way to divide houses into groups, where each group gets a mailbox. We calculate the total distance for each arrangement and pick the arrangement with the smallest total distance.
Here's how the algorithm would work step-by-step:
- Consider allocating mailboxes by placing the first mailbox at the first house.
- Then, consider placing the first mailbox covering the first two houses, and then the first three houses, and so on.
- For each of these potential locations for the first mailbox, consider all possible locations for the second mailbox.
- Continue this pattern of trying all possible positions for each mailbox until all mailboxes are allocated to groups of houses.
- For each arrangement, calculate the total distance each house is from its nearest mailbox.
- Compare the total distance for each arrangement, and select the allocation that minimizes the overall distance.
Code Implementation
def allocate_mailboxes_brute_force(houses, number_of_mailboxes):
number_of_houses = len(houses)
minimum_distance = float('inf')
def calculate_total_distance(mailbox_positions):
total_distance = 0
for house_position in houses:
minimum_house_distance = float('inf')
for mailbox_position in mailbox_positions:
minimum_house_distance = min(minimum_house_distance, abs(house_position - houses[mailbox_position]))
total_distance += minimum_house_distance
return total_distance
def find_minimum_distance(current_mailbox_index, current_mailbox_positions):
nonlocal minimum_distance
#If all mailboxes are placed, calculate the total distance
if current_mailbox_index == number_of_mailboxes:
total_distance = calculate_total_distance(current_mailbox_positions)
minimum_distance = min(minimum_distance, total_distance)
return
#Try placing mailbox at each possible house
start_position = 0 if not current_mailbox_positions else current_mailbox_positions[-1] # Each mailbox must cover at least one house
for mailbox_position in range(start_position, number_of_houses):
#Create a new arrangement with the new mailbox at this house.
new_mailbox_positions = current_mailbox_positions + [mailbox_position]
if len(new_mailbox_positions) <= number_of_mailboxes:
find_minimum_distance(current_mailbox_index + 1, new_mailbox_positions)
find_minimum_distance(0, [])
return minimum_distanceBig(O) Analysis
Optimal Solution
Approach
The problem asks us to minimize the total distance people have to walk to the nearest mailbox. The optimal approach involves cleverly identifying the best locations for mailboxes by considering the median house location within each group. By minimizing the distance for smaller groups, we build up to a solution that minimizes the overall distance.
Here's how the algorithm would work step-by-step:
- If we only have one mailbox, we want to put it in the location that minimizes the total walking distance for everyone. The best spot for one mailbox is at the median house location.
- If we have more mailboxes than houses, just put a mailbox at each house - the walking distance will be zero.
- Now, imagine we need to find the best spots for multiple mailboxes. We'll use the single mailbox case as a building block.
- Think about dividing the houses into groups, with each group getting its own mailbox. The key is finding the best way to split up these groups and where to put the mailbox for each group.
- We can find the optimal solution by building it up piece by piece. First, figure out the best spot for one mailbox serving the first few houses; then, figure out the best spot for two mailboxes serving a slightly larger group, and so on.
- To efficiently calculate the distance for each group, use previous calculations. We can calculate it more efficiently by subtracting out the part you no longer want and adding in the part you do.
- By working our way from small groups to larger groups, we can arrive at the best locations for all the mailboxes that minimize the total distance for everyone.
Code Implementation
def allocate_mailboxes(houses, number_of_mailboxes): houses.sort() number_of_houses = len(houses)
# If more mailboxes than houses, each house gets one if number_of_mailboxes >= number_of_houses:
return 0
# Cost to put one mailbox between house i and j inclusive cost = [[0] * number_of_houses for _ in range(number_of_houses)]
for i in range(number_of_houses):
for j in range(i, number_of_houses):
median = houses[(i + j) // 2]
for k in range(i, j + 1):
cost[i][j] += abs(houses[k] - median)
dp_table = [[float('inf')] * number_of_houses for _ in range(number_of_mailboxes + 1)]
# If only one mailbox, find the cost for each house
for i in range(number_of_houses):
dp_table[1][i] = cost[0][i]
# Build the solution iteratively for each mailbox count.
for mailbox_count in range(2, number_of_mailboxes + 1):
for house_index in range(mailbox_count - 1, number_of_houses):
# Find the optimal split between previous mailboxes and the current one
for split_point in range(mailbox_count - 2, house_index):
dp_table[mailbox_count][house_index] = min(dp_table[mailbox_count][house_index], \
dp_table[mailbox_count - 1][split_point] + cost[split_point + 1][house_index])
return dp_table[number_of_mailboxes][number_of_houses - 1]Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty houses array | Return 0 or throw an IllegalArgumentException, depending on the problem constraints. |
| Number of mailboxes (k) is zero or negative | Return 0 or throw an IllegalArgumentException as it's an invalid input. |
| Number of mailboxes (k) is greater than the number of houses | The minimal total distance will be zero, because each house has its own mailbox. |
| Houses array contains duplicate positions | The median calculation for the same position must consider multiple houses at the same location. |
| Houses array contains very large or very small coordinate values (integer overflow potential) | Use long data type to prevent integer overflow during distance calculations. |
| Houses are already sorted optimally for 1 mailbox (check if further partitioning will result in improved efficiency when k > 1) | The algorithm should be able to correctly identify and handle a pre-sorted optimal state. |
| When k = number of houses, distance is 0 | The code should return 0 directly without unnecessary calculations. |
| Houses array contains only one element | If k >= 1, the minimal total distance is 0, otherwise it is an invalid input. |