Alternating Groups I
EasyThere is a circle of red and blue tiles. You are given an array of integers colors. The color of tile i is represented by colors[i]:
colors[i] == 0means that tileiis red.colors[i] == 1means that tileiis blue.
Every 3 contiguous tiles in the circle with alternating colors (the middle tile has a different color from its left and right tiles) is called an alternating group.
Return the number of alternating groups.
Note that since colors represents a circle, the first and the last tiles are considered to be next to each other.
Example 1:
Input: colors = [1,1,1]
Output: 0
Explanation:
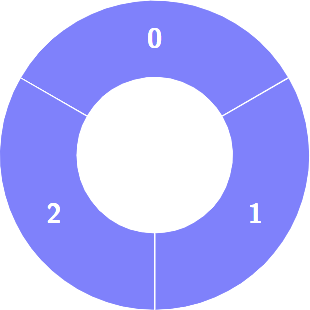
Example 2:
Input: colors = [0,1,0,0,1]
Output: 3
Explanation:
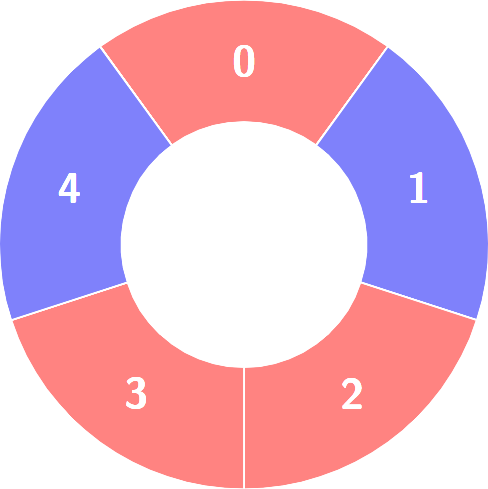
Alternating groups:
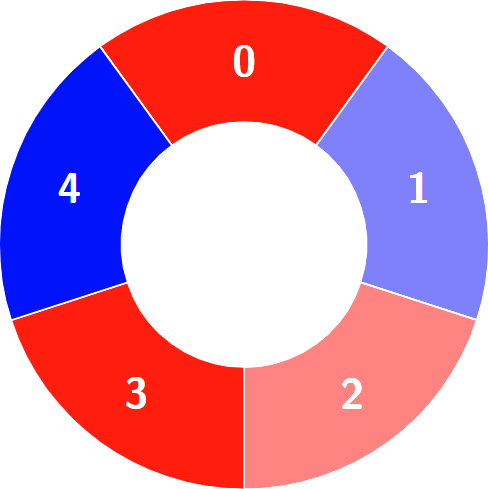
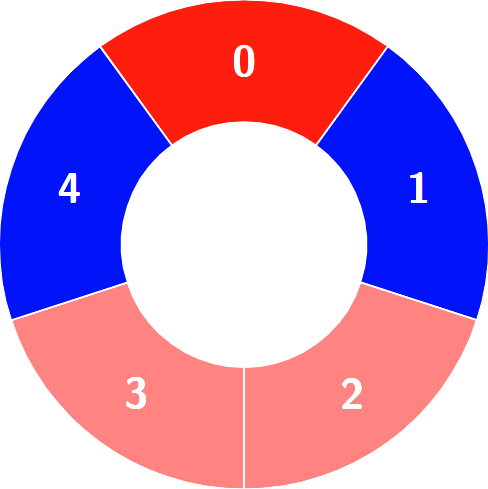

Constraints:
3 <= colors.length <= 1000 <= colors[i] <= 1
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum length of the binary string `s`?
- Can the input string `s` be empty or null?
- If there are multiple substrings with the same maximum number of alternating groups, should I return the number of groups from any of them?
- Is a single character considered an alternating group (e.g., "0" or "1")?
- If there is no substring with alternating groups (e.g., "0000" or "1111"), what should I return?
Brute Force Solution
Approach
The brute force approach to this problem involves checking every single possible way to split the given input into groups. We'll try all group combinations, and see if any meet the alternating condition.
Here's how the algorithm would work step-by-step:
- Start by assuming the first group contains only the first element.
- Then, assume the first group contains the first two elements, then the first three, and so on, until it contains all the elements.
- For each of these possibilities for the first group, consider all possible groupings for the remaining elements.
- Repeat the above step until all elements have been assigned to a group.
- For each complete grouping, check if the group sizes alternate between even and odd numbers. If they do, store that grouping as a potential solution.
- After considering all possible groupings, select the best solution according to whatever criteria the question asks for (e.g., shortest sequence, lexicographically smallest, etc.).
Code Implementation
def alternating_groups_brute_force(input_list):
all_groupings = []
def generate_groupings(current_index, current_grouping):
# Base case: all elements are assigned to a group
if current_index == len(input_list):
all_groupings.append(current_grouping)
return
# Iterate through all possible sizes for the next group
for group_size in range(1, len(input_list) - current_index + 1):
new_group = input_list[current_index:current_index + group_size]
# Recursively generate groupings for the remaining elements
generate_groupings(
current_index + group_size,
current_grouping + [new_group]
)
generate_groupings(0, [])
alternating_groupings = []
# Check all possible groupings for the alternating condition
for grouping in all_groupings:
is_alternating = True
for i in range(len(grouping) - 1):
if len(grouping[i]) % 2 == len(grouping[i+1]) % 2:
is_alternating = False
break
if is_alternating:
alternating_groupings.append(grouping)
if not alternating_groupings:
return []
# Return the first alternating grouping found
return alternating_groupings[0]
Big(O) Analysis
Optimal Solution
Approach
The key idea is to build the longest possible groups of alternating elements as we go. We achieve this by keeping track of how many groups are still available and prioritizing those that allow us to extend the current alternating sequence.
Here's how the algorithm would work step-by-step:
- Check if it is possible to form an alternating sequence with remaining groups of elements.
- Prioritize using larger groups of elements if using them doesn't ruin our chance to complete the sequence.
- If there are only a few elements of one group remaining, use them to finish the sequence.
- Repeat until no groups of elements are left.
Code Implementation
def alternating_groups(group_lengths):
alternating_sequence_length = 0
current_parity = 0 # 0 or 1 to track alternation
while True:
found_next = False
best_group_index = -1
best_group_length = -1
for index, group_length in enumerate(group_lengths):
if group_length > 0:
# Check the feasibility of adding group to current sequence
if index % 2 == current_parity:
if best_group_index == -1 or group_length > best_group_length:
best_group_index = index
best_group_length = group_length
found_next = True
if not found_next:
break
# Add the selected group length to the sequence
group_lengths[best_group_index] -= 1
alternating_sequence_length += 1
# Alternate the parity for the next group
current_parity = 1 - current_parity
return alternating_sequence_length
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty string input | Return 0, as there are no groups in an empty string. |
| Null string input | Return 0, handling null string gracefully by treating it as an empty string. |
| String with a single character (e.g., '0' or '1') | Return 1, as a single character forms a single group. |
| String with all identical characters (e.g., '0000' or '1111') | Return 1, as the entire string represents a single group. |
| String with two alternating groups (e.g., '0011' or '1100') | Return 2, correctly identifying the two alternating groups. |
| String with many alternating groups (e.g., '010101') | The algorithm must correctly count the groups, which should scale linearly to prevent Time Limit Exceeded. |
| String with mixed alternating and non-alternating groups (e.g., '0010110') | The solution must correctly identify the longest *substring* that alternates, requiring careful substring analysis. |
| Extremely long input string | Ensure the solution uses efficient substring analysis and doesn't have excessive memory usage to prevent Out of Memory errors. |