Alternating Groups II
Alternating Groups II #1 Most Asked
MediumThere is a circle of red and blue tiles. You are given an array of integers colors and an integer k. The color of tile i is represented by colors[i]:
colors[i] == 0means that tileiis red.colors[i] == 1means that tileiis blue.
An alternating group is every k contiguous tiles in the circle with alternating colors (each tile in the group except the first and last one has a different color from its left and right tiles).
Return the number of alternating groups.
Note that since colors represents a circle, the first and the last tiles are considered to be next to each other.
Example 1:
Input: colors = [0,1,0,1,0], k = 3
Output: 3
Explanation:
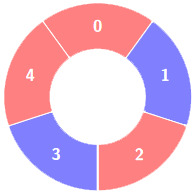
Alternating groups:
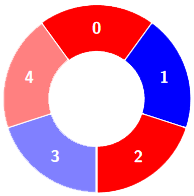

Example 2:
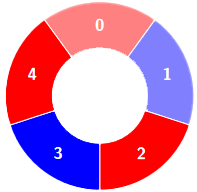
Input: colors = [0,1,0,0,1,0,1], k = 6
Output: 2
Explanation:

Alternating groups:


Example 3:
Input: colors = [1,1,0,1], k = 4
Output: 0
Explanation:
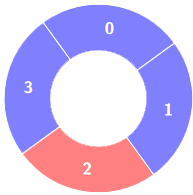
Constraints:
3 <= colors.length <= 1050 <= colors[i] <= 13 <= k <= colors.length
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum length of the input binary string `s`?
- Can the input string `s` be empty or null?
- If no valid partition exists (i.e., even a single substring violates the adjacent condition), what value should I return?
- By 'adjacent substrings', do you mean substrings that are directly next to each other in the final partitioned string, or substrings that were originally adjacent in the initial string `s`?
- Can you provide a few example inputs and their expected outputs to illustrate the desired behavior, especially edge cases or scenarios where multiple partitions are possible?
Brute Force Solution
Approach
The brute force method involves examining every single possible arrangement of groups within the data. We explore all starting points and lengths for the groups to see if the alternating pattern condition is met. Since every possibility is checked, this guarantees we will find the longest sequence if it exists.
Here's how the algorithm would work step-by-step:
- Consider every starting position within the data as the beginning of a potential alternating group sequence.
- For each starting position, consider every possible length of a potential first group.
- Then, for each first group, consider every possible length of a potential second group that immediately follows it.
- Continue this process of adding alternating groups and adjusting their lengths as long as the alternating pattern is maintained and you are still within the bounds of the data.
- Keep track of the longest alternating group sequence found so far.
- After exploring all possible starting positions and group lengths, report the longest alternating group sequence discovered.
Code Implementation
def find_longest_alternating_groups(data):
longest_sequence_length = 0
data_length = len(data)
for start_index in range(data_length):
for first_group_length in range(1, data_length - start_index + 1):
current_sequence_length = first_group_length
previous_group_value = data[start_index]
# Initialize the next group start position
next_group_start = start_index + first_group_length
while next_group_start < data_length:
for next_group_length in range(1, data_length - next_group_start + 1):
next_group_value = data[next_group_start]
# Check if the new group alternates
if next_group_value != previous_group_value:
current_sequence_length += next_group_length
previous_group_value = next_group_value
next_group_start += next_group_length
# Break to restart from the outter loop, length found
break
else:
# If next group does not alternate, sequence is broken
next_group_length = data_length
else:
# No valid next group found from this starting point
next_group_start = data_length
# Compare current sequence length
longest_sequence_length = max(longest_sequence_length, current_sequence_length)
return longest_sequence_lengthBig(O) Analysis
Optimal Solution
Approach
The problem asks to find the longest sequence that alternates between two groups. The key idea is to use a simple counting method while iterating through the sequence. We keep track of the length of the current group and update the maximum length whenever we find a valid alternating sequence.
Here's how the algorithm would work step-by-step:
- Start by assuming the first element belongs to the first group.
- Go through each element one by one.
- Check if the current element belongs to the same group as the previous element. If it does, the current sequence is broken, so reset the count of current sequence to 1.
- If the element belongs to a different group, it extends the alternating sequence, so increment the count.
- Keep track of the maximum length found so far during the process.
- Return the maximum length after checking all elements.
Code Implementation
def alternating_groups_ii(sequence):
max_length = 0
current_length = 0
if not sequence:
return 0
# Assume the first element belongs to group 1
previous_group = sequence[0] % 2
current_length = 1
max_length = 1
for i in range(1, len(sequence)):
current_element = sequence[i]
current_group = current_element % 2
# Check if the current element belongs to the same group
if current_group == previous_group:
current_length = 1
# Extend the alternating sequence
else:
current_length += 1
previous_group = current_group
# Update the maximum length
max_length = max(max_length, current_length)
return max_lengthBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty string input | Return 0, as there are no substrings to create. |
| String of length 1 | Return 1, as the single character forms a valid substring. |
| String with all '0's or all '1's | Return 1, as any partition would have adjacent substrings with the same number of 0s and 1s. |
| String with alternating '0' and '1' (e.g., '010101') | Return the length of the string, as each pair of characters can be a substring. |
| String with long sequences of '0's and '1's (e.g., '0000011111') | The solution should be able to determine the optimal split points to maximize the number of substrings. |
| String with '0' and '1' counts that are drastically different (e.g., '0000000001') | The optimal solution might involve making one large substring, or splitting to achieve alternating groups. |
| Maximum length string (consider memory and time complexity) | Ensure the algorithm's time and space complexity are efficient enough to handle large input strings, possibly O(n) time and O(1) or O(n) space depending on implementation. |
| String starts or ends with a very long sequence of identical characters | Algorithm should correctly identify the first/last splitting opportunity after the initial long sequence. |