Angle Between Hands of a Clock #8 Most Asked
MediumGiven two numbers, hour and minutes, return the smaller angle (in degrees) formed between the hour and the minute hand.
Answers within 10-5 of the actual value will be accepted as correct.
Example 1:

Input: hour = 12, minutes = 30 Output: 165
Example 2:
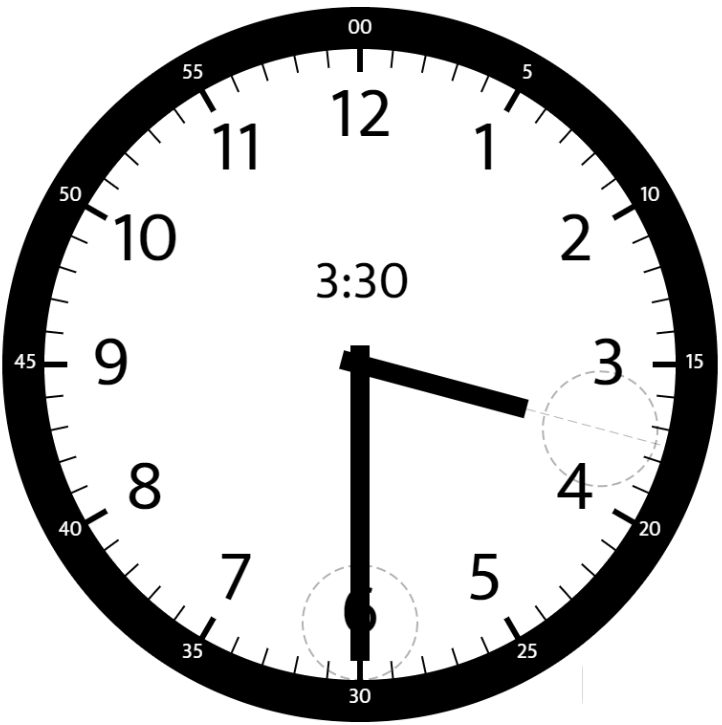
Input: hour = 3, minutes = 30 Output: 75
Example 3:

Input: hour = 3, minutes = 15 Output: 7.5
Constraints:
1 <= hour <= 120 <= minutes <= 59
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the valid ranges for the hour and minute inputs? Specifically, can the hour be outside the range of 1-12, and can the minutes be outside the range of 0-59?
- If the calculated angle has a fractional part, should I return an integer or a floating-point number, and to what precision should I round the result?
- If the hour or minute inputs are invalid, should I return a specific error code (e.g., -1), throw an exception, or assume that the inputs will always be valid?
- Are we working with a standard 12-hour clock, or could the hour represent something different that still needs to be converted to an angle?
- When calculating the angle, should I only consider the angle between 0 and 180 degrees, or are angles larger than 180 acceptable as long as the *smaller* of the two possible angles is ultimately returned?
Brute Force Solution
Approach
We want to find the angle between the hour and minute hands on a clock. The brute force approach involves calculating the positions of the hands for every possible minute and hour combination and then finding the angle between them.
Here's how the algorithm would work step-by-step:
- First, figure out how many degrees the minute hand moves for every minute that passes.
- Next, figure out how many degrees the hour hand moves for every hour that passes, and also how much it moves for each minute within that hour.
- Now, for every possible minute of the day (from 0 to 59), and for every possible hour (from 1 to 12), calculate the exact position of the minute hand in degrees.
- Do the same for the hour hand, taking into account both the hour and the minute to determine its position in degrees.
- Subtract the two degree measurements to find the angle between the hands.
- Make sure the angle is not greater than 180 degrees. If it is, subtract it from 360 degrees to get the smaller angle.
Code Implementation
def angle_between_hands(hour, minute):
minute_degrees_per_minute = 6
hour_degrees_per_hour = 30
hour_degrees_per_minute = 0.5
minute_hand_position = minute * minute_degrees_per_minute
# Hour hand moves based on the current hour and minutes passed in that hour
hour_hand_position = (hour % 12) * hour_degrees_per_hour + \
minute * hour_degrees_per_minute
angle = abs(hour_hand_position - minute_hand_position)
# We need to return the smaller angle between the two hands
if angle > 180:
angle = 360 - angle
return angleBig(O) Analysis
Optimal Solution
Approach
The goal is to calculate the angle between the hour and minute hands on a clock. We can do this efficiently by figuring out how far each hand is from the 12, and then finding the difference between those two positions.
Here's how the algorithm would work step-by-step:
- First, figure out where the minute hand is pointing. Every minute mark on the clock is a certain number of degrees around the circle.
- Next, determine where the hour hand is pointing. This is a bit trickier because the hour hand moves gradually between numbers as the minutes pass. So it's not just based on the hour, but also a fraction of the way to the next hour based on the minutes.
- Calculate the difference in degrees between where the minute hand is and where the hour hand is.
- The result might be a big angle (more than halfway around the clock). If so, take that angle away from the total degrees in a circle to get the smaller, more intuitive angle between the hands.
- Return the smaller angle.
Code Implementation
def angle_between_hands(hour, minutes):
# Calculate minute hand angle.
minute_angle = minutes * 6
# Hour hand moves fractionally.
hour_angle = (hour % 12 + minutes / 60) * 30
# Find the difference.
angle_difference = abs(hour_angle - minute_angle)
# Get the smaller angle.
if angle_difference > 180:
angle_difference = 360 - angle_difference
return angle_differenceBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Hour is negative | Return an error message or throw an exception, as hours cannot be negative. |
| Minute is negative | Return an error message or throw an exception, as minutes cannot be negative. |
| Hour is greater than 12 | Return an error message or throw an exception, as it is a 12-hour clock. |
| Minute is greater than 59 | Return an error message or throw an exception, as minutes cannot exceed 59. |
| Hour is 0 | Treat hour 0 as hour 12 when calculating the angle. |
| Minute is 0 | Calculate the hour hand position accurately when minutes are zero. |
| Hour is 12 and minute is 0 | The angle should be 0 as both hands point at the same position. |
| Floating point precision errors | Use Math.abs() to ensure a positive angle and handle potential inaccuracies when calculating the angle to determine the smaller one. |