Arranging Coins
Arranging Coins #2 Most Asked
EasyYou have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the ith row has exactly i coins. The last row of the staircase may be incomplete.
Given the integer n, return the number of complete rows of the staircase you will build.
Example 1:

Input: n = 5 Output: 2 Explanation: Because the 3rd row is incomplete, we return 2.
Example 2:
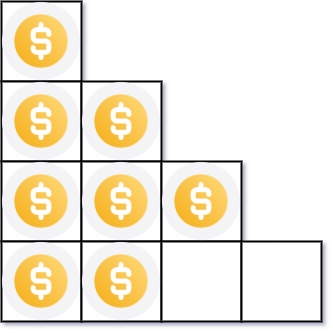
Input: n = 8 Output: 3 Explanation: Because the 4th row is incomplete, we return 3.
Constraints:
1 <= n <= 231 - 1
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of possible values for `n`? Is `n` guaranteed to be non-negative?
- If `n` is 0, should I return 0?
- Are we only interested in the number of *complete* rows? Or should I consider a partially filled last row?
- Is there a specific type I should return (e.g., int, long) considering the possible magnitude of the number of rows?
- Can you provide a few example inputs and their corresponding outputs to confirm my understanding of the problem?
Brute Force Solution
Approach
The brute force method for arranging coins involves building complete rows of coins one at a time. We start by trying to create one row, then two rows, and so on, until we find the maximum number of complete rows we can form with the given coins.
Here's how the algorithm would work step-by-step:
- Start by assuming we want to build only one complete row.
- Check if we have enough coins to build that row. If we do, that's a possible solution.
- Next, assume we want to build two complete rows. Calculate how many coins we need for that.
- Check if we have enough coins. If we do, that's another possible solution.
- Continue this process, increasing the number of rows we're trying to build each time.
- Stop when we find that we don't have enough coins to build the next complete row.
- The last number of rows for which we *did* have enough coins is the answer.
Code Implementation
def arrange_coins_brute_force(number_of_coins):
number_of_complete_rows = 0
coins_needed = 0
while True:
number_of_complete_rows += 1
# Calculate coins needed for the current number of rows.
coins_needed = number_of_complete_rows * (number_of_complete_rows + 1) // 2
# If we don't have enough coins, return the previous result.
if coins_needed > number_of_coins:
return number_of_complete_rows - 1
# If we have exactly enough coins, return current rows
if coins_needed == number_of_coins:
return number_of_complete_rowsBig(O) Analysis
Optimal Solution
Approach
The key to efficiently arranging the coins is to avoid testing every possibility. We want to find the largest complete staircase we can build with the given number of coins. We use a mathematical approach that dramatically reduces the computation needed.
Here's how the algorithm would work step-by-step:
- Think of building a staircase: 1 coin in the first row, 2 in the second, 3 in the third, and so on.
- We want to find out how many full rows (complete staircase) we can build.
- The total number of coins needed for a staircase of 'k' rows is roughly 'k squared divided by two'.
- Instead of adding up coins row by row, we can intelligently guess the number of rows.
- Check if this guess is too high or too low. If our guess uses too many coins, we lower our guess. If it uses too few, we increase our guess.
- Continue adjusting our guess until we find the number of rows that uses the most coins possible, but doesn't exceed the total number of available coins.
- The final correct guess is the maximum number of complete rows we can build with the coins we have.
Code Implementation
def arranging_coins(number_of_coins):
left_rows = 0
right_rows = number_of_coins
while left_rows <= right_rows:
mid_rows = left_rows + (right_rows - left_rows) // 2
# Calculate the total coins needed for 'mid_rows' rows.
coins_needed = mid_rows * (mid_rows + 1) // 2
if coins_needed == number_of_coins:
return mid_rows
elif coins_needed < number_of_coins:
# If coins needed is less, check for more rows
left_rows = mid_rows + 1
else:
# if coins needed exceeds available, reduce rows.
right_rows = mid_rows - 1
# Return right_rows because its the last valid complete row count
return right_rowsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| n is 0 | Return 0 since no complete rows can be formed with no coins. |
| n is 1 | Return 1, as one complete row can be formed with one coin. |
| n is a large number close to the maximum integer value (Integer Overflow Risk) | Use long data type for calculations or binary search to prevent potential integer overflow issues. |
| n results in a very large number of rows requiring many loop iterations | Optimize using binary search to find the solution efficiently to reduce time complexity. |
| n is a perfect square triangle number (e.g., 1, 3, 6, 10, 15) | The iterative or binary search algorithm should return the correct complete row count without issues. |
| n is slightly less than a perfect square triangle number | The iterative or binary search method will find the largest row number less than or equal to sqrt(2n + 0.25) - 0.5 |
| n is very small (e.g., 2, 3, 4) | The solution should still work correctly and return the correct number of rows. |
| The result of (k * (k + 1)) / 2 exceeds the maximum integer | Use long datatype for intermediate calculations of 'k * (k + 1)', or binary search which can be optimized to avoid explicit multiplication. |