As Far from Land as Possible
As Far from Land as Possible #2 Most Asked
MediumGiven an n x n grid containing only values 0 and 1, where 0 represents water and 1 represents land, find a water cell such that its distance to the nearest land cell is maximized, and return the distance. If no land or water exists in the grid, return -1.
The distance used in this problem is the Manhattan distance: the distance between two cells (x0, y0) and (x1, y1) is |x0 - x1| + |y0 - y1|.
Example 1:
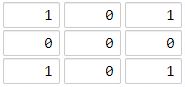
Input: grid = [[1,0,1],[0,0,0],[1,0,1]] Output: 2 Explanation: The cell (1, 1) is as far as possible from all the land with distance 2.
Example 2:
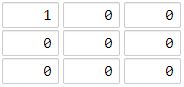
Input: grid = [[1,0,0],[0,0,0],[0,0,0]] Output: 4 Explanation: The cell (2, 2) is as far as possible from all the land with distance 4.
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 100grid[i][j]is0or1
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the grid, and what is the maximum possible size of the grid (number of rows and columns)?
- What values can each cell in the grid have besides 0 and 1; specifically, can there be any invalid values like negative numbers or nulls?
- If there is no land (all cells are 0s) or no water (all cells are 1s), what should the function return?
- Can I assume the grid is always a square (number of rows equals the number of columns), or can it be rectangular?
- By 'as far from land as possible', do you mean the maximum Manhattan distance to the nearest land cell, or should I consider other distance metrics?
Brute Force Solution
Approach
The brute force approach to finding the maximum distance from land involves checking every possible water cell. We calculate the shortest distance from each water cell to the nearest land cell, and ultimately find the largest of these distances. It's like exhaustively searching for the furthest point from any land.
Here's how the algorithm would work step-by-step:
- Go through each location in the grid one by one.
- If the current location is land, skip it and move to the next location.
- If the current location is water, find the distance to the closest land.
- To find the distance to the closest land, check the distance to *every* land location in the entire grid.
- Record the shortest distance found to any land location from this water location.
- After checking every water location and recording its shortest distance to land, compare all the recorded distances.
- The biggest distance recorded is the answer.
Code Implementation
def max_distance(grid):
rows = len(grid)
cols = len(grid[0])
max_water_distance = -1
for water_row in range(rows):
for water_col in range(cols):
if grid[water_row][water_col] == 1:
continue
shortest_distance_to_land = float('inf')
# Find the shortest distance to any land cell
for land_row in range(rows):
for land_col in range(cols):
if grid[land_row][land_col] == 1:
distance = abs(water_row - land_row) + abs(water_col - land_col)
shortest_distance_to_land = min(shortest_distance_to_land, distance)
# Update the maximum distance if necessary
if shortest_distance_to_land != float('inf'):
max_water_distance = max(max_water_distance, shortest_distance_to_land)
# Ensure at least one water cell is available
if max_water_distance == float('inf') or max_water_distance == 0 or max_water_distance == -1:
return -1
return max_water_distanceBig(O) Analysis
Optimal Solution
Approach
The key is to start from the land and expand outwards, layer by layer. Think of it like a wave spreading from the shore. This ensures we find the furthest water cell efficiently.
Here's how the algorithm would work step-by-step:
- First, find all the land cells in the grid. These are your starting points.
- Imagine these land cells as the first layer. Now, look at all the water cells directly next to the land. That's the next layer of cells to examine.
- For each water cell in this new layer, calculate its distance from the nearest land. Because you are expanding outwards, the distance will simply be one more than the previous layer's distance.
- Continue expanding outwards layer by layer, always looking at the water cells around the cells you just examined. Keep track of the maximum distance you find.
- When you've examined all the cells in the grid, the maximum distance you recorded is the answer. If there's no water (or no land) the furthest distance is -1.
Code Implementation
def max_distance(grid):
rows = len(grid)
cols = len(grid[0])
land_cells = []
for row in range(rows):
for col in range(cols):
if grid[row][col] == 1:
land_cells.append((row, col))
# If there is no land or all land, return -1
if not land_cells or len(land_cells) == rows * cols:
return -1
max_dist = -1
queue = land_cells[:] #start with all land
distance = 0
visited = set(land_cells)
while queue:
next_level = []
for row_index, col_index in queue:
# Explore neighbors
neighbors = [
(row_index - 1, col_index),
(row_index + 1, col_index),
(row_index, col_index - 1),
(row_index, col_index + 1)
]
for neighbor_row, neighbor_col in neighbors:
if 0 <= neighbor_row < rows and 0 <= neighbor_col < cols and (neighbor_row, neighbor_col) not in visited:
#Only visit unvisited water cells
if grid[neighbor_row][neighbor_col] == 0:
next_level.append((neighbor_row, neighbor_col))
visited.add((neighbor_row, neighbor_col))
if next_level: #only increase if there's a next level
distance += 1
queue = next_level
max_dist = distance
else:
queue = []
return max_distBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty grid or null grid | Return -1 immediately as there is no valid grid to process. |
| Grid with only one cell | If it's land, return -1; if it's water, return 0. |
| Grid with all land cells | Return -1, as there is no water to calculate distance from. |
| Grid with all water cells | Return the maximum possible distance, which is grid size dependent based on chosen approach (e.g. grid_size -1 with manhattan distance from edge). |
| Grid with maximum dimensions (e.g., 100x100) | Ensure that the BFS or dynamic programming solution does not exceed memory or time limits, potentially using iterative approach. |
| Grid with only one land cell | The water cell furthest from this single land cell is the furthest cell away which is handled by the BFS or similar approach. |
| Integer overflow when calculating distances | Use appropriate data types (e.g., long long in C++, long in Java) to avoid overflow, or use a distance representation that prevents large numbers like Manhattan distance. |
| Disjoint land masses | The BFS or dynamic programming approach should correctly handle disjoint land masses by propagating distances from all land cells concurrently. |