Best Position for a Service Centre
Hard
1 view
Topics:
Greedy Algorithms
A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that the sum of the euclidean distances to all customers is minimum.
Given an array positions where positions[i] = [xi, yi] is the position of the ith customer on the map, return the minimum sum of the euclidean distances to all customers.
In other words, you need to choose the position of the service center [xcentre, ycentre] such that the following formula is minimized:
Answers within 10-5 of the actual value will be accepted.
Example 1:
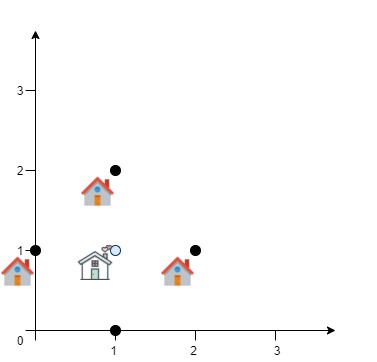
Input: positions = [[0,1],[1,0],[1,2],[2,1]] Output: 4.00000 Explanation: As shown, you can see that choosing [xcentre, ycentre] = [1, 1] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
Example 2:
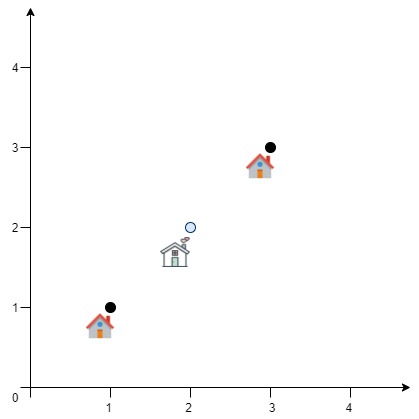
Input: positions = [[1,1],[3,3]] Output: 2.82843 Explanation: The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
Constraints:
1 <= positions.length <= 50positions[i].length == 20 <= xi, yi <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the size of the `positions` array, and what is the range of values for `xi` and `yi`?
- Can `xi` and `yi` be floating-point numbers or are they strictly integers?
- Is the input array `positions` ever empty or null? If so, what should I return?
- If there are multiple locations that result in the same minimum total distance, is any of them acceptable, or is there a specific tie-breaking condition?
- What distance metric should I use (e.g., Euclidean distance, Manhattan distance)? If Euclidean, how should I handle potential floating point precision issues when calculating distances?
Brute Force Solution
Approach
The brute force strategy is like trying out every possible location for the service center. We check how good each location is by calculating the total distance to all customers.
Here's how the algorithm would work step-by-step:
- Imagine a grid covering the whole area where the customers are located.
- For every single spot on that grid, pretend we put the service center there.
- Calculate the distance from that pretend service center to each and every customer.
- Add up all those distances to get a total distance for that pretend service center location.
- Do this for every single spot on the grid, keeping track of the total distance for each location.
- Once we've checked every spot on the grid, pick the spot that gave us the smallest total distance. That's our best location!
Code Implementation
def best_position_for_service_centre_brute_force(customer_locations): min_x = min(location[0] for location in customer_locations)
max_x = max(location[0] for location in customer_locations)
min_y = min(location[1] for location in customer_locations)
max_y = max(location[1] for location in customer_locations)
best_location = None
minimum_total_distance = float('inf')
# Iterate through all possible locations in the grid
for possible_x in range(min_x, max_x + 1):
for possible_y in range(min_y, max_y + 1):
total_distance = 0
# Calculate total distance to all customer locations for customer_x, customer_y in customer_locations: distance = ((possible_x - customer_x)**2 + (possible_y - customer_y)**2)**0.5
total_distance += distance
# Check if current location has smaller total distance if total_distance < minimum_total_distance:
minimum_total_distance = total_distance
best_location = (possible_x, possible_y)
return best_locationBig(O) Analysis
Time Complexity
O(N * X * Y) – Let N be the number of customers, X be the number of grid points along the x-axis, and Y be the number of grid points along the y-axis. The algorithm iterates through every grid point (service center location), which takes X * Y operations. For each grid point, the algorithm calculates the distance to each of the N customers. Therefore, the time complexity is O(N * X * Y), where N is the number of customers and X * Y represents all the points on the grid. This is because we are iterating over every possible location and calculating the sum of the distances from each possible location to all customers.
Space Complexity
O(1) – The provided brute force algorithm iterates through a grid covering the area where customers are located. For each grid point, it calculates the total distance to all customers but doesn't store the distances for all locations simultaneously. It only keeps track of the minimum total distance found so far and the corresponding location. Thus, the algorithm requires only a few variables to store the current location, the best location found, the current total distance, and the minimum total distance, resulting in constant auxiliary space.
Optimal Solution
Approach
The key idea is to find the best location for the service center that minimizes the total distance to all customers. Instead of checking every possible location, we can use a clever trick based on the median concept to quickly pinpoint the ideal spot.
Here's how the algorithm would work step-by-step:
- First, separate the locations of your customers into two groups: their east-west positions and their north-south positions.
- Find the middle value in the east-west positions. This is the east-west coordinate for the best service center location. To find the middle value, order the locations from west to east and pick the location in the very middle.
- Do the same for the north-south positions to find the north-south coordinate for the best service center location. Again, order the locations from south to north and pick the middle location.
- Combine these two middle values (east-west and north-south) to identify the optimal spot for the service center. This location minimizes the total distance to all the customers.
Code Implementation
def best_location(customer_locations):
horizontal_locations = [location[0] for location in customer_locations]
vertical_locations = [location[1] for location in customer_locations]
horizontal_locations.sort()
vertical_locations.sort()
# Calculate the median horizontal location.
number_of_customers = len(customer_locations)
if number_of_customers % 2 == 0:
median_horizontal_location = (
horizontal_locations[number_of_customers // 2 - 1] +
horizontal_locations[number_of_customers // 2]
) / 2
else:
median_horizontal_location = horizontal_locations[number_of_customers // 2]
# Calculate the median vertical location.
if number_of_customers % 2 == 0:
median_vertical_location = (
vertical_locations[number_of_customers // 2 - 1] +
vertical_locations[number_of_customers // 2]
) / 2
else:
median_vertical_location = vertical_locations[number_of_customers // 2]
# Combining medians gives the service center location.
service_center_location = (
median_horizontal_location,
median_vertical_location
)
return service_center_locationBig(O) Analysis
Time Complexity
O(n log n) – The algorithm's time complexity is dominated by the sorting steps. We sort the east-west positions and the north-south positions separately. Sorting n elements typically takes O(n log n) time using efficient algorithms like merge sort or quicksort. Since we perform two sorts, the total time is 2 * O(n log n), which simplifies to O(n log n). Finding the median after sorting takes O(1) time as we just access the middle element.
Space Complexity
O(N) – The algorithm involves sorting the east-west and north-south positions of the customers. This sorting operation typically requires creating auxiliary arrays or modifying the input array in place. Even if the original arrays are modified in place, many sorting algorithms (like merge sort) utilize a temporary array of size N, where N is the number of customers. Thus, the auxiliary space is proportional to the number of customer locations, N. Therefore, the space complexity is O(N).
Edge Cases
| Case | How to Handle |
|---|---|
| Empty input array | Return 0.0 as the minimum distance when no customers exist, as there is nothing to optimize. |
| Input array with a single customer | Return 0.0 as the minimum distance since the service center can be built at the customer's location. |
| All customer locations are identical | The algorithm should converge to the single location, resulting in a minimum distance of 0.0. |
| Customer locations form a straight line (highly skewed distribution) | The optimization algorithm should still converge to the optimal location along the line, minimizing total distance. |
| Customer locations with very large coordinates (potential overflow) | Use double data type for intermediate calculations and results to avoid integer overflow during distance calculations. |
| Customer locations with negative coordinates | The algorithm should handle negative coordinates correctly as they simply represent positions in the 2D plane relative to the origin. |
| Potential for infinite loop during optimization (e.g., oscillations) | Implement a maximum number of iterations or a convergence threshold (e.g., change in total distance is below a certain value) to prevent infinite loops. |
| Floating point precision issues affecting convergence | Use a small tolerance when comparing floating-point numbers to determine convergence to avoid premature termination or infinite loops due to minute variations. |
Explore Interview QuestionsGoogle Interview QuestionsMeta Interview QuestionsAmazon Interview QuestionsApple Interview QuestionsNetflix Interview Questions
Explore Jobs By LevelEntry-Level Software Engineer JobsMid-Level Software Engineer JobsSenior Software Engineer JobsStaff Software Engineer Jobs
