Binary Search Tree to Greater Sum Tree #19 Most Asked
MediumGiven the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.
As a reminder, a binary search tree is a tree that satisfies these constraints:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
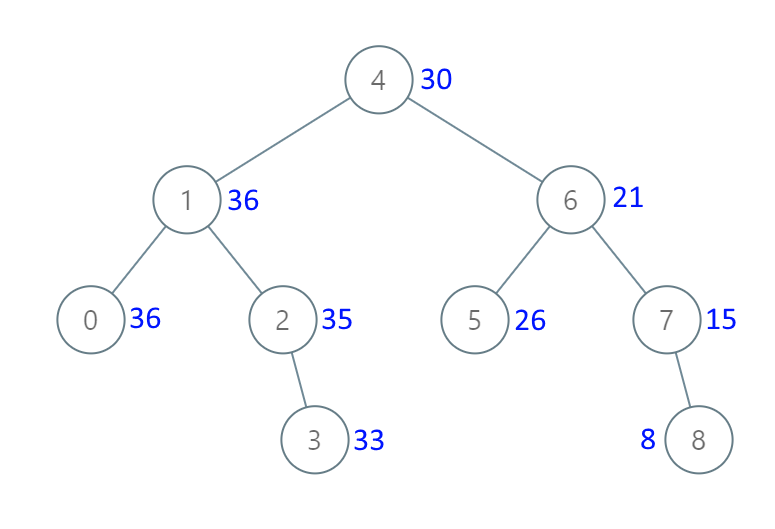
Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
Example 2:
Input: root = [0,null,1] Output: [1,null,1]
Constraints:
- The number of nodes in the tree is in the range
[1, 100]. 0 <= Node.val <= 100- All the values in the tree are unique.
Note: This question is the same as 538: https://leetcode.com/problems/convert-bst-to-greater-tree/
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values that the nodes in the BST can have? Are negative values allowed?
- Can the BST be empty, or can it contain only a single node?
- Are there duplicate values allowed in the BST? If so, how should they be handled when calculating the greater sum?
- Is the input guaranteed to be a valid Binary Search Tree?
- Should I modify the existing tree in-place, or can I create a new tree with the updated values?
Brute Force Solution
Approach
The brute force method for this tree problem involves recalculating sums for each node. We're essentially going to ignore any smart shortcuts and compute everything from scratch for every single value in the tree.
Here's how the algorithm would work step-by-step:
- For each individual value in the tree, we need to figure out what it needs to become.
- To do that, we will look at every other value in the tree to see if it is bigger than the value we are currently working on.
- If another value *is* bigger, we add it to a running total.
- After we have checked every single other value in the tree, that running total becomes the *new* value for the original value we were working on.
- We then repeat this process for every single value in the tree. When finished, the original tree has now been transformed.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def bst_to_gst_brute_force(root):
all_node_values = []
def inorder_traversal(node):
if not node:
return
inorder_traversal(node.left)
all_node_values.append(node.val)
inorder_traversal(node.right)
inorder_traversal(root)
# Store the original values for later re-assignment
original_node_values = all_node_values.copy()
# This function modifies the tree in-place
def transform_tree(node):
if not node:
return
transform_tree(node.left)
# Calculate new value by summing larger values
new_value = 0
for other_value in original_node_values:
if other_value > node.val:
new_value += other_value
node.val = new_value + node.val
transform_tree(node.right)
transform_tree(root)
return rootBig(O) Analysis
Optimal Solution
Approach
The key idea is to traverse the binary search tree in a specific order. We want to modify each node's value to be the sum of all nodes greater than or equal to it in the original tree. We can achieve this using a reverse inorder traversal.
Here's how the algorithm would work step-by-step:
- Start at the rightmost node of the tree (the largest value in the tree).
- Keep track of a running sum, initialized to zero.
- As you visit each node, add its original value to the running sum.
- Update the node's value to be the current running sum.
- Move to the parent node or the next largest node in the tree (the inorder predecessor).
- Repeat the process for each node until you have traversed the entire tree.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
class Solution:
def bstToGst(self, root):
running_sum = 0
def reverseInorderTraversal(root):
nonlocal running_sum
if root:
# Traverse the right subtree first (largest values).
reverseInorderTraversal(root.right)
# Update running sum with current node's value.
running_sum += root.value
# Update the node's value with the running sum.
root.value = running_sum
# Traverse the left subtree.
reverseInorderTraversal(root.left)
reverseInorderTraversal(root)
return rootBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree (root is null) | Return null immediately; an empty tree remains empty after the transformation. |
| Tree with only one node | The single node's value becomes itself, and the tree is returned without modification. |
| Tree with all identical values | Each node's value will become n * node.val where n is the number of nodes. |
| Highly skewed tree (e.g., all nodes on the right) | The algorithm should still correctly calculate the cumulative sum from right to left. |
| Tree with negative values | The cumulative sum can become negative and should be correctly calculated and assigned. |
| Tree with zero values | Zero values should be correctly included in the cumulative sum. |
| Large tree potentially causing stack overflow (if using recursion) | Use iterative inorder traversal (right-to-left) to avoid recursion depth issues. |
| Integer overflow when calculating the cumulative sum | Use a larger data type (e.g., long) to store the cumulative sum to prevent overflow. |