Binary Tree Coloring Game
MediumTwo players play a turn based game on a binary tree. We are given the root of this binary tree, and the number of nodes n in the tree. n is odd, and each node has a distinct value from 1 to n.
Initially, the first player names a value x with 1 <= x <= n, and the second player names a value y with 1 <= y <= n and y != x. The first player colors the node with value x red, and the second player colors the node with value y blue.
Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an uncolored neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)
If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.
You are the second player. If it is possible to choose such a y to ensure you win the game, return true. If it is not possible, return false.
Example 1:
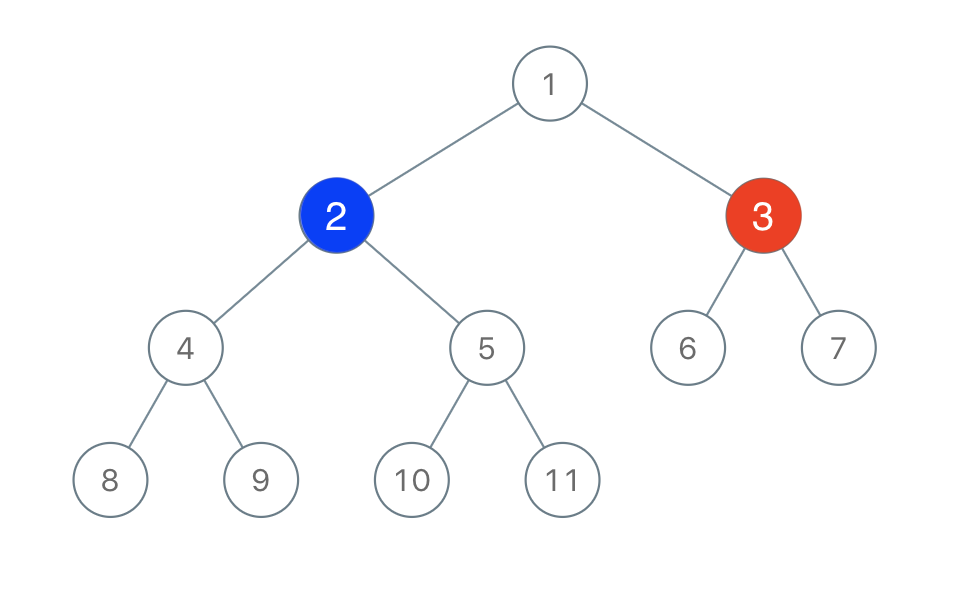
Input: root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3 Output: true Explanation: The second player can choose the node with value 2.
Example 2:
Input: root = [1,2,3], n = 3, x = 1 Output: false
Constraints:
- The number of nodes in the tree is
n. 1 <= x <= n <= 100nis odd.- 1 <= Node.val <= n
- All the values of the tree are unique.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the nodes in the binary tree? Are they positive integers, or can they be negative or zero?
- Is the given tree guaranteed to be a valid binary tree, or should I handle cases where the structure is invalid (e.g., cycles)?
- If the chosen node (by the first player) results in a situation where the second player cannot win, what should my function return? Should I return true if *any* move of the first player can lead to a win for the second player?
- How is the binary tree represented? Is it given as a root node of a custom `TreeNode` class, or is it represented in some other way?
- What are the constraints on the size of the tree (number of nodes)? I want to consider the potential for stack overflow with recursive approaches.
Brute Force Solution
Approach
In this game, two players take turns coloring nodes in a binary tree. The brute force strategy involves exploring every possible move for both players to determine if the first player can guarantee a win.
Here's how the algorithm would work step-by-step:
- Start by considering all possible nodes the first player can choose to color.
- For each of those choices, imagine the second player then picks a node from the remaining uncolored nodes.
- Continue this process, alternating between players, exploring every possible sequence of moves until the whole tree is colored.
- After each possible sequence of moves, check to see who won the game, based on how many connected nodes each player colored.
- If any of the first player's initial choices leads to a situation where they win, regardless of what the second player does, then the first player can win the game.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
def binary_tree_coloring_game_brute_force(root, number_of_nodes, first_player_choice):
def count_colored_nodes(node, colored_nodes):
if not node:
return 0
count = 0
if node.value in colored_nodes:
count += 1
count += count_colored_nodes(node.left, colored_nodes)
count += count_colored_nodes(node.right, colored_nodes)
return count
def find_node(root, target):
if not root:
return None
if root.value == target:
return root
node = find_node(root.left, target)
if node:
return node
return find_node(root.right, target)
def check_win(first_player_nodes, second_player_nodes):
first_player_count = 0
second_player_count = 0
first_player_count = count_colored_nodes(root, first_player_nodes)
second_player_count = count_colored_nodes(root, second_player_nodes)
return first_player_count > second_player_count
def get_all_nodes(root):
nodes = []
if not root:
return nodes
nodes.append(root.value)
nodes.extend(get_all_nodes(root.left))
nodes.extend(get_all_nodes(root.right))
return nodes
def can_first_player_win(available_nodes, first_player_nodes, second_player_nodes, turn):
if not available_nodes:
return check_win(first_player_nodes, second_player_nodes)
if turn == 0:
# First player's turn.
for node_choice in available_nodes:
new_available_nodes = available_nodes[:]
new_available_nodes.remove(node_choice)
new_first_player_nodes = first_player_nodes[:]
new_first_player_nodes.add(node_choice)
# Recursively call the function to explore the next move
if can_first_player_win(new_available_nodes, new_first_player_nodes, second_player_nodes, 1):
return True
return False
else:
# Second player's turn.
for node_choice in available_nodes:
new_available_nodes = available_nodes[:]
new_available_nodes.remove(node_choice)
new_second_player_nodes = second_player_nodes[:]
new_second_player_nodes.add(node_choice)
# After second player's turn, it's first player's turn
if not can_first_player_win(new_available_nodes, first_player_nodes, new_second_player_nodes, 0):
return False
# Second player can always force a win
return True
# Get all the nodes in the tree to represent availble choices
all_nodes_in_tree = get_all_nodes(root)
available_nodes = set(all_nodes_in_tree)
# Color the first player's choice and make it unavailable
first_player_nodes = set()
first_player_nodes.add(first_player_choice)
available_nodes.remove(first_player_choice)
# Represent second player's nodes
second_player_nodes = set()
# Check if first player can win
return can_first_player_win(available_nodes, first_player_nodes, second_player_nodes, 1)Big(O) Analysis
Optimal Solution
Approach
The goal is to pick a node strategically so the other player can't create a larger connected group of their color. We want to choose a node that, when removed, leaves the largest possible disconnected subtree. By controlling the largest portion, we limit the opponent's ability to dominate the tree.
Here's how the algorithm would work step-by-step:
- Find the node picked by the first player.
- Consider the parent of this node, its left child, and its right child. These are the key areas to consider.
- Calculate the number of nodes in the subtree of the left child of the chosen node.
- Calculate the number of nodes in the subtree of the right child of the chosen node.
- Calculate the number of nodes in the subtree including the parent of the chosen node (which equals the total number of nodes minus 1 minus the left and right subtrees).
- Compare the sizes of these three groups (left subtree, right subtree, parent subtree).
- Pick the node from the largest of the three groups. This blocks the first player from getting more than half of the nodes.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def binary_tree_coloring_game(root, number_of_nodes, node_chosen_by_player1):
left_subtree_size = 0
right_subtree_size = 0
def count_subtree_nodes(node):
if not node:
return 0
return 1 + count_subtree_nodes(node.left) + count_subtree_nodes(node.right)
def find_node(node, target):
if not node:
return None
if node.val == target:
return node
left_search = find_node(node.left, target)
if left_search:
return left_search
return find_node(node.right, target)
chosen_node = find_node(root, node_chosen_by_player1)
# Count nodes in left subtree.
left_subtree_size = count_subtree_nodes(chosen_node.left)
# Count nodes in right subtree.
right_subtree_size = count_subtree_nodes(chosen_node.right)
# Calculate size of the parent subtree
parent_subtree_size = number_of_nodes - left_subtree_size - right_subtree_size - 1
# Check if any subtree is larger than half the total nodes
if left_subtree_size > number_of_nodes // 2 or \
right_subtree_size > number_of_nodes // 2 or \
parent_subtree_size > number_of_nodes // 2:
return True
else:
return FalseBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node | Return false immediately if the root is null as no coloring is possible. |
| Tree with only one node | Return false since player 1 cannot choose x such that it leaves two components for player 2 to win. |
| x is the root node | Calculate the sizes of the left and right subtrees of the root and check if either is greater than n/2. |
| x is a leaf node | Calculate the size of the remaining tree after removing x and its edge to the parent; player 2 can win if parent side is greater than n/2. |
| x has only one child | Compare the size of the subtree rooted at x's child and the size of the rest of the tree with n/2 to see if player 2 can win. |
| Skewed tree (e.g., linked list) | The tree traversal should still correctly calculate subtree sizes regardless of the tree's shape. |
| Large tree (n close to maximum integer value) | Ensure the size calculations (subtree counts) don't result in integer overflow by using appropriate data types. |
| n is even and x is chosen such that each of the three components has size exactly n/3 | This represents a scenario where player 2 cannot win, thus the code needs to handle returning false. |