Binary Tree Paths
Binary Tree Paths #5 Most Asked
EasyGiven the root of a binary tree, return all root-to-leaf paths in any order.
A leaf is a node with no children.
Example 1:
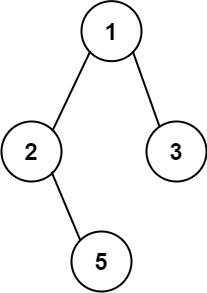
Input: root = [1,2,3,null,5] Output: ["1->2->5","1->3"]
Example 2:
Input: root = [1] Output: ["1"]
Constraints:
- The number of nodes in the tree is in the range
[1, 100]. -100 <= Node.val <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can node values be negative, zero, or positive?
- What should be returned if the root is null?
- Is the binary tree guaranteed to be a valid binary tree, or should I handle potentially malformed trees?
- Is there a maximum depth or number of nodes that I should be aware of?
- If there are multiple root-to-leaf paths, is there any required order for the paths in the output list?
Brute Force Solution
Approach
The brute force method for finding all paths in a binary tree involves exploring every possible route from the top (root) to the bottom (leaves). We build each path step-by-step and store it. We continue this process until every potential path has been created and checked.
Here's how the algorithm would work step-by-step:
- Begin at the very top of the tree, at the starting point.
- Consider one possible direction to go down the tree.
- Write down that direction as part of a potential path.
- Keep going down the tree, adding each new direction you take to your path.
- If you reach the bottom of the tree, the path you've written down is a complete path.
- Save this complete path.
- Go back up a step and see if there is a different direction to go.
- If there is another direction, explore it and write down that new path.
- Repeat these steps until you've explored every possible direction from every point in the tree, and written down every path you could find.
Code Implementation
def binary_tree_paths(root):
all_paths = []
current_path = []
def find_paths(node, current_path):
if not node:
return
# Add the current node's value to the path
current_path.append(str(node.val))
# If it's a leaf node, save the path
if not node.left and not node.right:
all_paths.append('->'.join(current_path))
# Crucial to backtrack and not contaminate other paths.
current_path.pop()
return
# Explore the left subtree
find_paths(node.left, current_path)
# Explore the right subtree
find_paths(node.right, current_path)
# Backtrack: remove the current node from the path
# after exploring its children.
current_path.pop()
find_paths(root, current_path)
return all_pathsBig(O) Analysis
Optimal Solution
Approach
The optimal approach involves exploring the tree in a specific manner, building paths as we go. Instead of creating all possible paths independently, we modify a single path as we traverse the tree, effectively reusing memory and computation.
Here's how the algorithm would work step-by-step:
- Begin at the root node of the tree and consider the path from the root to the current node.
- As you move from a node to its child, add the child to the current path.
- If you reach a node with no children (a leaf node), save the current path as a complete path from the root to a leaf.
- When you've explored a node and its children, remove the node from the end of the current path. This lets you backtrack and explore other branches.
- Continue this process until all nodes have been explored, generating all root-to-leaf paths.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
def binary_tree_paths(root):
result_paths = []
current_path = []
def traverse_tree(node):
if not node:
return
current_path.append(str(node.value))
# If it's a leaf node, save the path.
if not node.left and not node.right:
result_paths.append("->".join(current_path))
else:
# Explore the left and right subtrees.
traverse_tree(node.left)
traverse_tree(node.right)
# Backtrack: remove the current node to explore other paths.
current_path.pop()
traverse_tree(root)
return result_pathsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node | Return an empty list immediately as there are no paths. |
| Single node tree (root is also a leaf) | Return a list containing only the root node's value as a string. |
| Tree with only left children (highly skewed) | The solution should traverse all left children correctly, building the path string. |
| Tree with only right children (highly skewed) | The solution should traverse all right children correctly, building the path string. |
| Tree with large depth (potential stack overflow in recursive solutions) | Consider an iterative solution using a stack to avoid stack overflow issues with deeply nested trees. |
| Nodes with negative values | The algorithm should handle negative node values without modification, since values are treated as strings in the paths. |
| Nodes with zero value | The algorithm should handle zero node values without modification. |
| Tree with a very large number of nodes (memory usage) | Ensure the solution's space complexity remains reasonable, especially concerning the number and length of path strings created. |