Binary Tree Tilt #3 Most Asked

Easy

2 views

Topics:

TreesRecursion

Given the root of a binary tree, return the sum of every tree node's tilt.

The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if the node does not have a right child.

Example 1:

Input: root = [1,2,3]
Output: 1
Explanation: 
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1

Example 2:

Input: root = [4,2,9,3,5,null,7]
Output: 15
Explanation: 
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15

Example 3:

Input: root = [21,7,14,1,1,2,2,3,3]
Output: 9

Constraints:

The number of nodes in the tree is in the range [0, 10⁴].
-1000 <= Node.val <= 1000

Try coding it in LeetCode

Binary Tree Tilt #3 Most Asked

Easy

Indeed

2 views

Topics:

TreesRecursion

Given the root of a binary tree, return the sum of every tree node's tilt.

The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if the node does not have a right child.

Example 1:

Input: root = [1,2,3]
Output: 1
Explanation: 
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1

Example 2:

Input: root = [4,2,9,3,5,null,7]
Output: 15
Explanation: 
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15

Example 3:

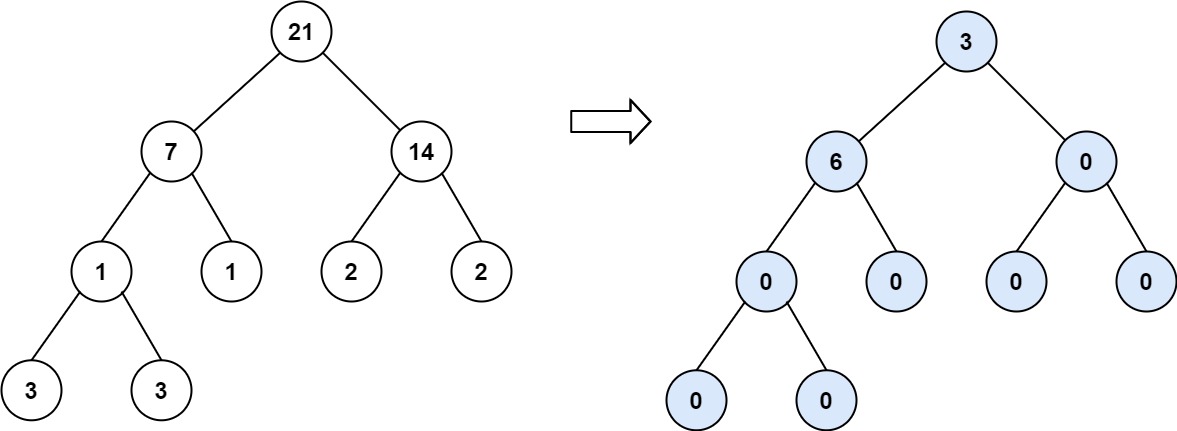
Input: root = [21,7,14,1,1,2,2,3,3]
Output: 9

Constraints:

The number of nodes in the tree is in the range [0, 10⁴].
-1000 <= Node.val <= 1000

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the range of values for the node values in the binary tree? Can they be negative?
Is it possible for the binary tree to be empty (null)? What should the tilt be in that case?
By 'tilt of the whole tree', do you mean the sum of the tilts of all the individual nodes in the tree?
Are we only dealing with integer values for the node values and the resulting tilts?
Is the tree guaranteed to be a valid binary tree, or do I need to handle cases where the structure might be incorrect (e.g., cycles)?

Brute Force Solution

Approach

The brute force approach to find the tilt of a binary tree involves examining every single node in the tree. For each node, we'll calculate the tilt by computing the sum of the node's left subtree and the sum of the node's right subtree, then finding the absolute difference. Finally, we add up all these differences.

Here's how the algorithm would work step-by-step:

Start at the very top node of the tree.
For that node, figure out the total value of all the nodes in its left side.
Separately, figure out the total value of all the nodes in its right side.
Subtract the smaller total from the bigger total, always getting a positive number or zero. This is the tilt for that node.
Remember this tilt value, and then repeat steps 2-4 for every other node in the tree. It doesn't matter what order you visit the other nodes.
Once you've calculated the tilt for every single node in the tree, add all those tilt values together.
The final sum of all the tilts is the total tilt of the binary tree.

Code Implementation

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def find_tree_tilt(root):
    total_tilt = 0

    def calculate_subtree_sum(node):
        if not node:
            return 0
        return node.val + calculate_subtree_sum(node.left) + calculate_subtree_sum(node.right)

    def traverse_tree(node):
        nonlocal total_tilt
        
        if not node:
            return

        #Calculate the sum of the left subtree
        left_subtree_sum = calculate_subtree_sum(node.left)

        #Calculate the sum of the right subtree
        right_subtree_sum = calculate_subtree_sum(node.right)

        # The tilt is the absolute difference of the subtree sums.
        tilt = abs(left_subtree_sum - right_subtree_sum)

        # Add to the running sum.
        total_tilt += tilt

        traverse_tree(node.left)
        traverse_tree(node.right)

    traverse_tree(root)
    return total_tilt

Big(O) Analysis

Time Complexity

O(n²) – The algorithm iterates through each of the n nodes in the binary tree. For each node, it calculates the sum of its left and right subtrees. Calculating the sum of a subtree requires traversing all nodes within that subtree. In the worst-case scenario, where the tree is heavily skewed, calculating the subtree sum could involve visiting a significant portion of the remaining nodes in the tree, approaching n nodes. Thus, for each of the n nodes, we potentially perform an O(n) operation, leading to a time complexity of O(n * n) or O(n²).

Space Complexity

O(N) – The brute force approach uses recursion. In the worst-case scenario, the binary tree resembles a linked list, causing the recursive calls to stack up to a depth of N, where N is the number of nodes in the tree. Each recursive call consumes memory on the call stack for function arguments, local variables, and return address. Therefore, the auxiliary space complexity is determined by the maximum depth of the recursion, which can be N in the worst case.

Optimal Solution

Approach

The most efficient way to find the total tilt of a binary tree involves calculating the tilt of each node and accumulating the results in a single pass. We achieve this by using a method that figures out the sum of values in the subtrees while simultaneously calculating each node's tilt. This prevents revisiting nodes and keeps the process efficient.

Here's how the algorithm would work step-by-step:

Start at the bottom of the tree and work upwards. For each node, we need to know the sum of the values in its left subtree and the sum of the values in its right subtree.
Calculate the 'tilt' of the current node. The tilt is the absolute difference between the sum of the left subtree and the sum of the right subtree.
Add the current node's tilt to a running total that keeps track of the total tilt of the entire tree.
Before moving up the tree, return the sum of the current node's value plus the sum of the values in its left and right subtrees. This makes the sums available to the node's parent.
Repeat this process for every node in the tree, and the running total will give you the total tilt of the entire tree.

Code Implementation

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def findTilt(self, root: TreeNode) -> int:
        total_tilt_sum = 0

        def calculate_node_sum_and_tilt(node: TreeNode) -> int:
            nonlocal total_tilt_sum

            if not node:
                return 0

            # Calculate sum of left and right subtrees
            left_subtree_sum = calculate_node_sum_and_tilt(node.left)

            right_subtree_sum = calculate_node_sum_and_tilt(node.right)

            # Tilt is absolute difference between left and right
            current_node_tilt = abs(left_subtree_sum - right_subtree_sum)

            total_tilt_sum += current_node_tilt

            # Return sum of current node and its subtrees
            return node.val + left_subtree_sum + right_subtree_sum

        calculate_node_sum_and_tilt(root)
        return total_tilt_sum

Big(O) Analysis

Time Complexity

O(n) – The algorithm visits each node in the binary tree exactly once. For each node, it performs a constant amount of work: calculating the tilt (absolute difference of subtree sums) and adding it to the total tilt. The number of nodes in the tree is 'n'. Therefore, the time complexity is directly proportional to the number of nodes, resulting in O(n) time complexity.

Space Complexity

O(N) – The dominant space complexity factor in this algorithm stems from the recursion depth. The algorithm traverses the binary tree using recursion, and in the worst-case scenario (e.g., a skewed tree), the recursion stack can grow to the height of the tree, which can be N, where N is the number of nodes. Therefore, the auxiliary space used by the recursion stack is proportional to N. This results in O(N) space complexity.

Edge Cases

Case	How to Handle
Null root node	Return 0 as the tilt of a null tree is defined as 0.
Single node tree	Return 0 as a single node tree has no tilt.
Tree with all nodes having value 0	This should be handled correctly as the sum of subtrees would be 0, and tilt would be calculated accurately.
Tree with large positive and negative values causing potential integer overflow in sum	Use a larger integer type (e.g., long) to store subtree sums to avoid potential overflow.
Complete binary tree with maximum depth and node values	Ensure that the recursion depth doesn't exceed the stack limit and algorithm is efficient enough for large trees by considering iterative solutions.
Skewed tree (left or right)	Verify the solution handles the unbalanced nature of the tree efficiently, avoiding worst-case O(n^2) time complexity in some implementations.
Tree with negative node values	The algorithm should correctly handle negative values during the summation of subtrees and tilt calculation.
Tree with extreme value differences between left and right subtrees	Confirm that the absolute difference calculation doesn't cause unexpected behavior with very large numbers; use appropriate data types.

Null root node

How to Handle:

Return 0 as the tilt of a null tree is defined as 0.

Single node tree

How to Handle:

Return 0 as a single node tree has no tilt.

Tree with all nodes having value 0

How to Handle:

This should be handled correctly as the sum of subtrees would be 0, and tilt would be calculated accurately.

Tree with large positive and negative values causing potential integer overflow in sum

How to Handle:

Use a larger integer type (e.g., long) to store subtree sums to avoid potential overflow.

Complete binary tree with maximum depth and node values

How to Handle:

Ensure that the recursion depth doesn't exceed the stack limit and algorithm is efficient enough for large trees by considering iterative solutions.

Skewed tree (left or right)

How to Handle:

Verify the solution handles the unbalanced nature of the tree efficiently, avoiding worst-case O(n^2) time complexity in some implementations.

Tree with negative node values

How to Handle:

The algorithm should correctly handle negative values during the summation of subtrees and tilt calculation.

Tree with extreme value differences between left and right subtrees

How to Handle:

Confirm that the absolute difference calculation doesn't cause unexpected behavior with very large numbers; use appropriate data types.