Binary Tree Zigzag Level Order Traversal
MediumGiven the root of a binary tree, return the zigzag level order traversal of its nodes' values. (i.e., from left to right, then right to left for the next level and alternate between).
Example 1:
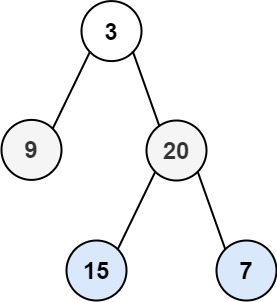
Input: root = [3,9,20,null,null,15,7] Output: [[3],[20,9],[15,7]]
Example 2:
Input: root = [1] Output: [[1]]
Example 3:
Input: root = [] Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 2000]. -100 <= Node.val <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the nodes in the binary tree?
- What should I return if the root is null or the tree is empty?
- Is the binary tree guaranteed to be a valid binary tree?
- Can I assume that the node values are integers?
- Do I need to preserve the structure of the original tree, or is it acceptable if my solution modifies it?
Brute Force Solution
Approach
We're given a tree and need to visit its levels in a zigzag pattern. The brute force approach is like exploring every single possible path through the tree, level by level, and figuring out the zigzag order after visiting each level. This means considering every combination of left-to-right and right-to-left traversals for each level.
Here's how the algorithm would work step-by-step:
- First, explore the tree level by level using a standard method, making sure to visit every single node.
- For each level, record the order in which you visited the nodes when going from left to right.
- Also, for each level, record the order in which you visited the nodes when going from right to left.
- Now, try every possible combination of traversal orders for each level. For example, the first level could be left-to-right, and the second could be right-to-left, or vice versa. Try all such combinations.
- For each of these combinations, build the final zigzag order list. That is, for a given combination, add nodes to the list based on whether you are going left to right or right to left on a level.
- Finally, after exploring all possible combinations of traversal orders, choose one of the zigzag order lists that follows the given rules (first level usually left to right).
Code Implementation
from collections import deque
def binary_tree_zigzag_level_order_traversal_brute_force(root):
if not root:
return []
levels = []
queue = deque([root])
while queue:
level_size = len(queue)
current_level_nodes = []
for _ in range(level_size):
node = queue.popleft()
current_level_nodes.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
levels.append(current_level_nodes)
zigzag_result = []
# Try all possible combinations of directions.
for level_index, level_nodes in enumerate(levels):
if level_index % 2 == 0:
zigzag_result.append(level_nodes)
else:
# Reverse the order of the nodes for odd levels.
zigzag_result.append(level_nodes[::-1])
return zigzag_resultBig(O) Analysis
Optimal Solution
Approach
We want to visit the tree level by level, but alternate the direction we read each level. The key idea is to use a data structure that allows us to easily add and remove nodes while keeping track of the current level and direction.
Here's how the algorithm would work step-by-step:
- Start by putting the root of the tree into a special container that holds nodes to be processed.
- While the container is not empty, process all nodes in the container one level at a time.
- For each level, create a temporary holding place to store the values of the nodes on that level.
- Depending on whether it's a left-to-right or right-to-left level, add the node values to the temporary holding place in the correct order.
- After processing all nodes in the current level, switch the reading direction (from left-to-right to right-to-left, or vice versa).
- Prepare the container for the next level by adding all the children of the current level's nodes to it. Add the children in order from left to right.
- Add the temporary holding place with node values for the current level to our final result.
- Repeat until all levels have been processed and the container is empty.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def zigzag_level_order(root):
if not root:
return []
results = []
nodes_to_process = [root]
left_to_right = True
while nodes_to_process:
current_level_values = []
next_level_nodes = []
# Process all nodes at the current level.
for node in nodes_to_process:
current_level_values.append(node.val)
# Reverse the order if traversing right-to-left.
if not left_to_right:
current_level_values.reverse()
results.append(current_level_values)
# Add children for the next level's processing.
for node in nodes_to_process:
if node.left:
next_level_nodes.append(node.left)
if node.right:
next_level_nodes.append(node.right)
# Switch direction for the next level.
left_to_right = not left_to_right
nodes_to_process = next_level_nodes
return resultsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree root | Return an empty list immediately since there is nothing to traverse. |
| Tree with only one node (root) | Return a list containing a list with only the root's value. |
| Completely unbalanced tree (left or right skewed) | The solution using level order traversal with a queue handles skewed trees correctly as it processes each level regardless of balance. |
| Tree with all nodes having the same value | The algorithm correctly traverses and adds all nodes regardless of value redundancy to the result list. |
| Tree with a large number of nodes (scalability) | The level-order traversal's time complexity is O(N) where N is the number of nodes, so it should scale adequately with a queue-based implementation. |
| Integer overflow if node values are extremely large | While unlikely, consider using a larger data type (e.g., long) for node values if overflow is a potential concern based on the problem constraints. |
| Deeply unbalanced tree causing stack overflow with a recursive approach (if used) | An iterative approach using a queue is preferred to avoid potential stack overflow issues with recursion for deeply unbalanced trees. |
| Tree with negative node values | The solution correctly handles negative node values as they are treated as regular integer values during traversal. |