Brick Wall #13 Most Asked
MediumThere is a rectangular brick wall in front of you with n rows of bricks. The ith row has some number of bricks each of the same height (i.e., one unit) but they can be of different widths. The total width of each row is the same.
Draw a vertical line from the top to the bottom and cross the least bricks. If your line goes through the edge of a brick, then the brick is not considered as crossed. You cannot draw a line just along one of the two vertical edges of the wall, in which case the line will obviously cross no bricks.
Given the 2D array wall that contains the information about the wall, return the minimum number of crossed bricks after drawing such a vertical line.
Example 1:
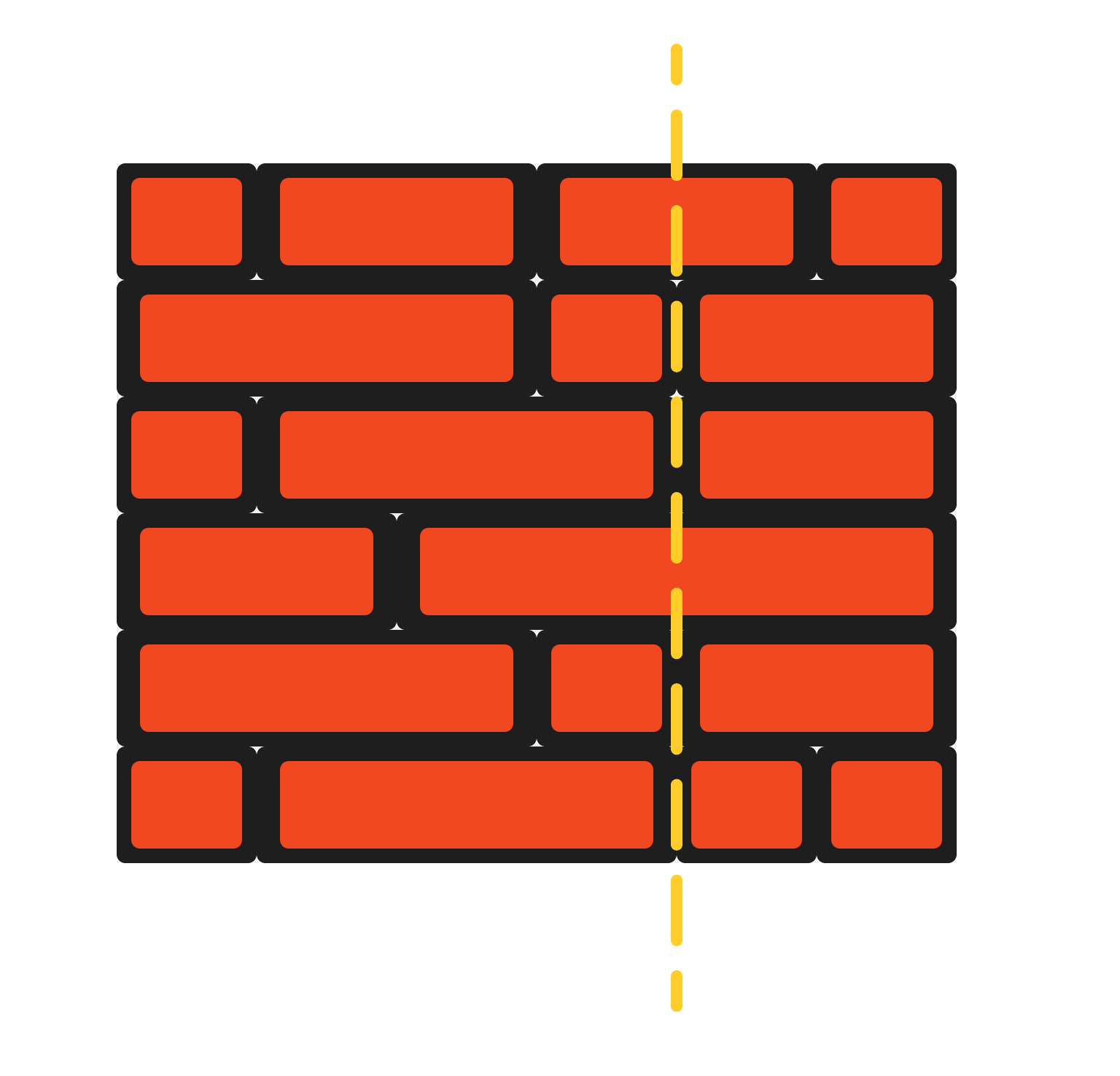
Input: wall = [[1,2,2,1],[3,1,2],[1,3,2],[2,4],[3,1,2],[1,3,1,1]] Output: 2
Example 2:
Input: wall = [[1],[1],[1]] Output: 3
Constraints:
n == wall.length1 <= n <= 1041 <= wall[i].length <= 1041 <= sum(wall[i].length) <= 2 * 104sum(wall[i])is the same for each rowi.1 <= wall[i][j] <= 231 - 1
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions constraints for the 2D array `wall` (number of rows and bricks per row)?
- Can the width of a brick be zero, or can a row be empty?
- Are the brick widths guaranteed to be positive integers?
- What should I return if the wall is empty or if all rows have only one brick?
- Is the sum of brick widths in each row guaranteed to be the same?
Brute Force Solution
Approach
The brute force approach to the brick wall problem means we're going to try every single possible vertical line placement. We'll examine each possible location for a line, count how many bricks that line would cut through, and keep track of the minimum number of cuts.
Here's how the algorithm would work step-by-step:
- Consider a vertical line at every possible position where a brick ends within each row.
- For each possible vertical line position, go through each row of bricks.
- Count how many bricks each vertical line would intersect.
- Keep track of the number of intersected bricks for each vertical line position.
- Find the vertical line position that intersects the fewest bricks.
- The minimum number of intersected bricks represents the fewest cuts needed to draw a line through the wall.
Code Implementation
def brick_wall_brute_force(wall):
if not wall:
return 0
number_of_rows = len(wall)
maximum_wall_width = sum(wall[0])
minimum_cuts = number_of_rows
# Iterate through all possible vertical line positions
for line_position in range(1, maximum_wall_width):
cuts_for_this_position = 0
# Iterate through each row to count cuts
for row in wall:
brick_edge_position = 0
for brick_length in row:
brick_edge_position += brick_length
# Check if the line cuts through a brick
if brick_edge_position == line_position:
break
if brick_edge_position > line_position:
cuts_for_this_position += 1
break
#Update minimum_cuts if needed
minimum_cuts = min(minimum_cuts, cuts_for_this_position)
return minimum_cutsBig(O) Analysis
Optimal Solution
Approach
The goal is to find the vertical line that crosses the fewest bricks. The trick is to realize that instead of focusing on the lines themselves, we should focus on the gaps between the bricks in each row.
Here's how the algorithm would work step-by-step:
- Go through each row of the brick wall.
- For each row, keep track of where the gaps are by adding up the widths of the bricks.
- Count how many times each gap position appears across all rows.
- Find the gap position that appears most often.
- The number of rows minus the most frequent gap count is the minimum number of bricks crossed by a vertical line.
Code Implementation
def least_bricks_crossed(wall):
gap_counts = {}
for row in wall:
gap_position = 0
# Iterate up to the second to last brick to find gaps
for i in range(len(row) - 1):
gap_position += row[i]
# Store the number of times we see each gap
if gap_position not in gap_counts:
gap_counts[gap_position] = 0
gap_counts[gap_position] += 1
max_gap_frequency = 0
# Find the most frequent gap.
for gap_position in gap_counts:
max_gap_frequency = max(max_gap_frequency, gap_counts[gap_position])
# Subtract the most frequent gap from the total rows.
return len(wall) - max_gap_frequency
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty wall (no rows) | Return 0, as no bricks can be crossed in an empty wall. |
| Wall with only one row and a single brick. | Return 0, as the line cannot be drawn on the edges, so it won't cross any brick. |
| Wall with only one row and multiple bricks | The line can be drawn at the common edge with the maximum frequency, then the crossed bricks will be row count (1) - max frequency. |
| All bricks in the wall are of width 1 | The vertical line will have the maximum number of intersections, the number of rows in the wall. |
| All rows are the same configuration of brick widths. | The intersection frequency calculation will correctly determine the best vertical line placement to minimize crossed bricks. |
| Wall with very large width bricks causing potential integer overflow in intermediate sums. | Use a data type with a larger range (e.g., long) to store the cumulative brick widths to prevent overflow. |
| Rows with different total widths (invalid input). | Check that each row has the same total width when summed; if not, either throw an error or proceed with caution, noting that the 'end' of each row is different. |
| Wall with a very large number of rows. | The solution should scale linearly with the number of rows, as it iterates through them once to calculate edge frequencies. |