Champagne Tower
MediumWe stack glasses in a pyramid, where the first row has 1 glass, the second row has 2 glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
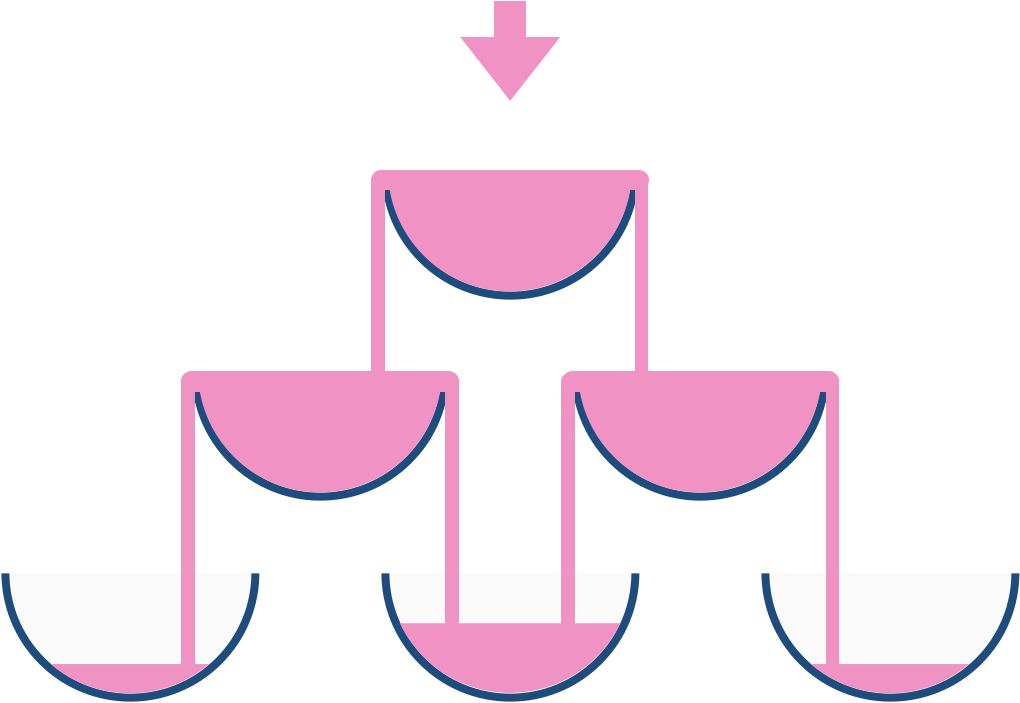
Now after pouring some non-negative integer cups of champagne, return how full the jth glass in the ith row is (both i and j are 0-indexed.)
Example 1:
Input: poured = 1, query_row = 1, query_glass = 1 Output: 0.00000 Explanation: We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
Example 2:
Input: poured = 2, query_row = 1, query_glass = 1 Output: 0.50000 Explanation: We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
Example 3:
Input: poured = 100000009, query_row = 33, query_glass = 17 Output: 1.00000
Constraints:
0 <= poured <= 1090 <= query_glass <= query_row < 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- How many rows are in the champagne tower? What is the data type and range for the poured champagne?
- If we pour more champagne than the tower can hold, what value should I return for a glass that's overflowing?
- Can 'poured' be zero or negative? What should be the behavior in those cases?
- What is the desired precision for the returned value (e.g., number of decimal places)?
- Are the row and glass indices 0-indexed or 1-indexed?
Brute Force Solution
Approach
The brute force method for the champagne tower problem involves directly simulating pouring champagne level by level. We track how much champagne ends up in each glass by simulating the pouring process and calculating how excess champagne flows to the glasses below. This approach works by explicitly checking the result of pouring into each glass and distributing the overflow.
Here's how the algorithm would work step-by-step:
- Start by pouring the given amount of champagne into the top glass of the tower.
- If the top glass overflows, divide the extra champagne equally between the two glasses in the next level below.
- For each glass in the subsequent levels, if a glass receives more than its capacity (which is one glass worth of champagne), split the extra champagne equally between the two glasses directly beneath it in the next level.
- Continue this process level by level, simulating the pouring and overflowing until we have gone down far enough that the target glass has potentially received champagne. Remember each glass only holds one glass of champagne.
- After simulating the pouring and overflowing, check how much champagne is in the target glass. If it has one or more glasses of champagne in it, it means that the glass is completely full and therefore contains one glass of champagne. Return the appropriate value.
Code Implementation
def champagne_tower_brute_force(poured, query_row, query_glass):
tower = [[0.0] * (level + 1) for level in range(query_row + 1)]
tower[0][0] = float(poured)
for row_index in range(query_row):
for glass_index in range(row_index + 1):
# Only distribute overflow if the glass has champagne
if tower[row_index][glass_index] > 1:
overflow = (tower[row_index][glass_index] - 1.0) / 2.0
tower[row_index+1][glass_index] += overflow
tower[row_index+1][glass_index+1] += overflow
# Limit each glass to one glass of champagne
tower[row_index][glass_index] = 1.0
return min(1.0, tower[query_row][query_glass])Big(O) Analysis
Optimal Solution
Approach
The best way to solve the champagne tower problem is to simulate the pouring process, tracking how much champagne ends up in each glass. We don't need to calculate all possibilities, just focus on where the champagne flows from top to bottom.
Here's how the algorithm would work step-by-step:
- Imagine the tower as a structure where each glass can hold only one cup of champagne.
- Start pouring champagne from the very top glass.
- If a glass overflows, split the extra champagne evenly between the two glasses directly below it.
- Continue this process row by row, simulating how the champagne flows down the tower.
- Once all the pouring is done, check the glass you are interested in.
- If the glass has more than one cup of champagne (meaning it overflowed), it's full. Otherwise, it contains the amount of champagne calculated.
Code Implementation
def champagneTower(poured, query_row, query_glass):
tower = [[0.0] * (i + 1) for i in range(query_row + 1)]
# Initialize the top glass with the poured champagne.
tower[0][0] = float(poured)
for row in range(query_row):
for glass in range(row + 1):
# If a glass has more than 1 cup, distribute excess.
if tower[row][glass] > 1:
excess = (tower[row][glass] - 1.0) / 2.0
tower[row][glass] = 1.0
# Distribute the overflow to the glasses below.
tower[row + 1][glass] += excess
tower[row + 1][glass + 1] += excess
# Ensure the returned value is not greater than 1.
return min(1.0, tower[query_row][query_glass])Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Poured glasses is zero. | Return 0.0 as no champagne is poured. |
| Query row or query glass is negative. | Return 0.0 as row and glass indices cannot be negative. |
| Query row is much larger than poured. | Return 0.0 as the glasses in lower rows will overflow before filling a distant row. |
| Poured is extremely large, causing floating-point overflow. | Check for and handle infinity values, returning the maximum capacity (1.0) if overflow occurs. |
| Query row and glass are within the bounds of poured glasses. | Calculate the amount of champagne in that glass using the given rules. |
| Query glass is out of bounds for a given row (glass index exceeds row number). | Return 0.0 as the glass does not exist in that row. |
| Poured champagne exactly fills all glasses up to query_row. | The queried glass may contain either 1.0 or 0.0 depending on the amount of overflow from the row above. |
| Floating point precision issues. | Use a small epsilon value when comparing floating point numbers for equality to avoid incorrect comparisons due to precision errors. |