Check Completeness of a Binary Tree #7 Most Asked
MediumGiven the root of a binary tree, determine if it is a complete binary tree.
In a complete binary tree, every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
Example 1:
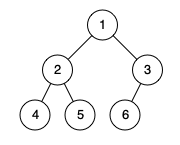
Input: root = [1,2,3,4,5,6]
Output: true
Explanation: Every level before the last is full (ie. levels with node-values {1} and {2, 3}), and all nodes in the last level ({4, 5, 6}) are as far left as possible.
Example 2:
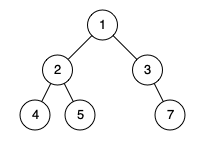
Input: root = [1,2,3,4,5,null,7] Output: false Explanation: The node with value 7 isn't as far left as possible.
Constraints:
- The number of nodes in the tree is in the range
[1, 100]. 1 <= Node.val <= 1000
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values that a node can hold?
- Can the tree be empty or contain only a single node?
- Is the input guaranteed to be a valid binary tree?
- What should I return if the tree is empty?
- By completeness, do you mean a complete binary tree where all levels are completely filled except possibly the last level, which is filled from left to right?
Brute Force Solution
Approach
We can check if a binary tree is complete by exploring the tree level by level. The brute-force approach here involves exploring every possible node sequence in a level-order traversal and meticulously checking whether the tree's structure adheres to the complete binary tree property.
Here's how the algorithm would work step-by-step:
- Visualize the binary tree and imagine traversing it level by level, like reading a book line by line.
- Keep track of all the nodes you encounter in this level-by-level order.
- As you go, if you find a node that's missing (it should be there according to the rules of a complete tree), immediately stop and say the tree is not complete.
- If you get to a missing node after encountering nodes that are not full (do not have two children) then the tree is not complete.
- Otherwise, keep going through the entire tree.
- If you reach the end of the tree without finding any violations of the complete tree structure, then you can confidently say the tree is complete.
Code Implementation
from collections import deque
def is_complete_tree(root):
if not root:
return True
queue = deque([root])
found_null = False
while queue:
current_node = queue.popleft()
if current_node is None:
found_null = True
else:
#If we found null before and now we find a node
if found_null:
return False
queue.append(current_node.left)
queue.append(current_node.right)
return TrueBig(O) Analysis
Optimal Solution
Approach
The goal is to figure out if there are any missing nodes at the bottom of the tree *before* the last node we encounter. We will traverse the tree level by level, checking each node to see if it invalidates the completeness of the tree.
Here's how the algorithm would work step-by-step:
- Begin checking the tree starting from the very top node.
- Use a method to visit each node one level at a time, going from left to right within each level.
- As you are checking each level, keep track of whether you've seen a 'missing' node. A 'missing' node is a spot where a node *should* exist, according to the tree's structure, but doesn't.
- If you encounter a node *after* you have already seen a 'missing' node, then the tree is not complete.
- If you reach the end of the tree (you've checked all the nodes), and you haven't seen any nodes appear *after* a 'missing' node, then the tree *is* complete.
Code Implementation
from collections import deque
def is_complete_tree(root):
if not root:
return True
queue = deque([root])
seen_null_node = False
while queue:
current_node = queue.popleft()
if current_node is None:
seen_null_node = True
else:
# If we've seen a missing node, tree is incomplete
if seen_null_node:
return False
queue.append(current_node.left)
# Append right child to queue for processing
queue.append(current_node.right)
return TrueBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root | Return True immediately since an empty tree is considered complete. |
| Single node tree | Return True, as a single node tree is complete. |
| Perfectly complete tree | The algorithm should efficiently identify it as complete without early termination. |
| Tree missing nodes only at the lowest level (complete) | The algorithm should correctly identify this type of tree as complete by correctly checking for null nodes after a full node is encountered. |
| Tree missing nodes in the middle of the tree (not complete) | The algorithm should detect this and return False upon encountering a non-full node before the last level. |
| Left-skewed tree | The algorithm, especially if using level-order traversal, should handle the skew without incorrectly identifying it as incomplete if the last level nodes are as far left as possible. |
| Right-skewed tree | Similarly to a left-skewed tree, the right-skewed tree must be handled properly to determine if it's incomplete due to mid-level missing nodes. |
| Large tree (potential memory issues) | Level-order traversal might consume significant memory for wide trees; consider if an alternative traversal method could be more memory efficient or if memory constraints become a concern. |