Check if Every Row and Column Contains All Numbers
EasyAn n x n matrix is valid if every row and every column contains all the integers from 1 to n (inclusive).
Given an n x n integer matrix matrix, return true if the matrix is valid. Otherwise, return false.
Example 1:
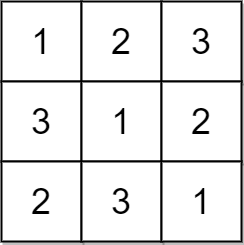
Input: matrix = [[1,2,3],[3,1,2],[2,3,1]] Output: true Explanation: In this case, n = 3, and every row and column contains the numbers 1, 2, and 3. Hence, we return true.
Example 2:
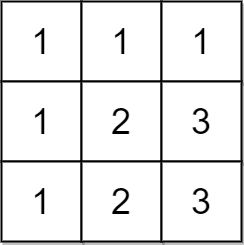
Input: matrix = [[1,1,1],[1,2,3],[1,2,3]] Output: false Explanation: In this case, n = 3, but the first row and the first column do not contain the numbers 2 or 3. Hence, we return false.
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 1001 <= matrix[i][j] <= n
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum possible value of 'n' in the n x n matrix?
- Is the input matrix guaranteed to be square (n x n)?
- Can I assume that the matrix will always contain integers between 1 and n, or should I validate that?
- If the matrix is empty (n=0), what should the return value be?
- Are there any memory constraints I should be aware of, or should I optimize for space complexity in addition to time complexity?
Brute Force Solution
Approach
We're given a grid of numbers and we want to see if every row and every column contains all the numbers from 1 up to the size of the grid. The brute force way checks each row and column individually to see if it has all the needed numbers. It's like manually verifying each row and column one by one.
Here's how the algorithm would work step-by-step:
- First, consider the rows of the grid. We'll look at each row separately.
- For each row, we need to make sure it has all the numbers from 1 to the size of the grid. To do this, we can check if each number from 1 to the size of the grid appears in that row.
- If we find even one row that is missing a number, or has a number that is out of range, we know the whole grid fails the check.
- If all the rows pass the check, then we do the same thing for the columns.
- For each column, we again make sure it has all the numbers from 1 to the size of the grid, just like we did for the rows. We check if each number from 1 to the size of the grid appears in that column.
- If we find even one column that is missing a number, or has a number that is out of range, we know the whole grid fails the check.
- If both all the rows and all the columns pass the check, then we can say that the grid satisfies the condition. In short, we exhaustively examine each row and each column to make sure they all contain the appropriate numbers.
Code Implementation
def check_if_every_row_and_column_contains_all_numbers(matrix):
matrix_size = len(matrix)
# Check if each row contains all numbers from 1 to matrix_size
for row in matrix:
for number_to_check in range(1, matrix_size + 1):
if number_to_check not in row:
return False
# If all rows passed, check the columns
for column_index in range(matrix_size):
column = []
for row_index in range(matrix_size):
column.append(matrix[row_index][column_index])
# Verify that the current column has the numbers from 1 to matrix_size
for number_to_check in range(1, matrix_size + 1):
if number_to_check not in column:
return False
return TrueBig(O) Analysis
Optimal Solution
Approach
The problem requires us to verify if a grid has all numbers from 1 to N in each row and each column. The efficient strategy involves using sets to quickly track the presence of each number within a row or column and avoid repeated checks. This avoids nested loops that check every possible arrangement.
Here's how the algorithm would work step-by-step:
- For each row, create a set to store the numbers found in that row.
- Add each number from the row into its respective set.
- After processing each row, check if the set contains all the numbers from 1 to N. If not, the condition is not met and we can stop.
- Repeat the same process for each column, using a separate set for each column.
- If all rows and all columns meet the condition of having all numbers from 1 to N, then the grid satisfies the requirement.
Code Implementation
def check_if_every_row_and_column_contains_all_numbers(matrix):
matrix_size = len(matrix)
# Check each row to confirm it contains all numbers from 1 to N.
for row in matrix:
row_values = set()
for value in row:
row_values.add(value)
if len(row_values) != matrix_size:
return False
# Check each column to confirm it contains all numbers from 1 to N.
for column_index in range(matrix_size):
column_values = set()
for row_index in range(matrix_size):
column_values.add(matrix[row_index][column_index])
# If a column does not contain all numbers, return false.
if len(column_values) != matrix_size:
return False
return TrueBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty matrix | Return true (or false) immediately as an empty matrix technically satisfies (or violates) the condition, depending on interpretation, but should be handled explicitly. |
| Non-square matrix (m x n where m != n) | Return false immediately as the problem specifies an n x n matrix and the condition cannot be satisfied. |
| Matrix with n=1 (single element) | Return true because a single element matrix trivially satisfies the condition that the single row and single column contain the number 1. |
| Matrix with numbers outside the range [1, n] | Return false, since numbers must be in the range 1 to n, indicating an invalid input. |
| Large matrix size (n is very large) | Ensure the solution has optimal time complexity (e.g., O(n^2)) to avoid timeouts, and be mindful of potential memory usage. |
| Matrix with all identical values | Return false unless the value is 1 and n=1, as otherwise, rows and columns cannot contain all numbers from 1 to n. |
| Input matrix is not of type Integer | Return false or throw an IllegalArgumentException because the problem specifies an integer matrix. |
| Integer overflow when n is large | Ensure that any calculations involving n don't overflow the integer data type by using appropriate data types or checks. |