Check If It Is a Straight Line #14 Most Asked
EasyYou are given an array coordinates, coordinates[i] = [x, y], where [x, y] represents the coordinate of a point. Check if these points make a straight line in the XY plane.
Example 1:
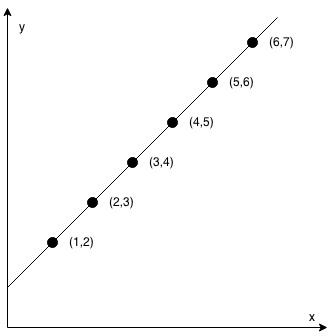
Input: coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]] Output: true
Example 2:
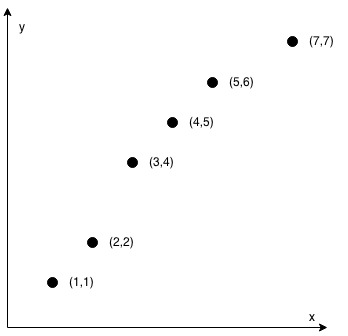
Input: coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]] Output: false
Constraints:
2 <= coordinates.length <= 1000coordinates[i].length == 2-10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4coordinatescontains no duplicate point.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the expected data type of the coordinates? Are they integers or floating-point numbers?
- What is the minimum number of coordinates I can expect in the input? Can I assume at least two points will always be provided?
- If all points are the same (e.g., duplicate coordinates), should I return true or false? How should I handle a single point?
- If the points do not form a straight line, what should I return? Should I return false, or is there a specific error value I should return instead?
- Is there a maximum value for the coordinates, and should I be concerned about potential integer overflow issues during slope calculations?
Brute Force Solution
Approach
To determine if a set of points form a straight line using the brute force method, we'll check every possible pair of points to define a line, then verify if all other points fall on that same line. This involves comparing each point against the line defined by our initial pair to ensure they are collinear. We'll repeat this for every possible starting pair to confirm our findings.
Here's how the algorithm would work step-by-step:
- Pick the first two points from the given set of points.
- These two points define a line. Determine the slope of the line created by these two points.
- Now, take each remaining point, one at a time, and check if it lies on the same line as the first two points. To do this, see if the slope between that point and any of the first two points is the same as the slope of the line defined by the first two points.
- If you find a point that does *not* lie on the same line, then the set of points does not form a straight line, and you can stop immediately.
- If you reach the end and all other points lie on the same line as the initial two points, then these points may be collinear; however, you are not done yet, you must repeat this process with other pairs of points.
- Repeat the entire process starting with a *different* pair of points from the original set.
- Keep repeating this process, taking every pair of points as the defining line and check against all remaining points.
- If, and only if, for *every* possible pair, all other points lie on the line defined by the pair, then you can be certain that all the points lie on a single straight line.
Code Implementation
def check_if_it_is_a_straight_line(points):
number_of_points = len(points)
if number_of_points <= 2:
return True
for i in range(number_of_points):
for j in range(i + 1, number_of_points):
# Select two points to define a line.
point_one_x, point_one_y = points[i]
point_two_x, point_two_y = points[j]
# Calculate slope; handle vertical line case
if point_two_x - point_one_x == 0:
slope = float('inf')
else:
slope = (point_two_y - point_one_y) / (point_two_x - point_one_x)
for k in range(number_of_points):
if k != i and k != j:
point_three_x, point_three_y = points[k]
# Check if point lies on the line.
if point_one_x == point_three_x and point_one_x == point_two_x:
if point_two_x != point_three_x:
return False
elif point_two_x - point_one_x == 0:
return False
else:
current_slope = (point_three_y - point_one_y) / (point_three_x - point_one_x) if (point_three_x - point_one_x) != 0 else float('inf')
# Must check for division by zero when calculating slope
if (point_three_x - point_one_x) == 0 and slope != float('inf'):
return False
elif (point_three_x - point_one_x) != 0 and slope == float('inf'):
return False
elif current_slope != slope:
return False
# If all pairs of points check out, return True.
return TrueBig(O) Analysis
Optimal Solution
Approach
To determine if a set of points form a straight line, we can use the concept of slope. The key idea is that all points on a straight line will have the same slope relative to any other point on that line. Therefore, we can compare the slopes between different pairs of points.
Here's how the algorithm would work step-by-step:
- First, handle the trivial case where there are very few points (like two points). In this case, they always form a straight line.
- Pick the first two points from the set of points. Calculate the slope between these two points. This will be our reference slope.
- Now, iterate through the remaining points in the set.
- For each remaining point, calculate the slope between the first point and the current point.
- Compare this new slope with the reference slope we calculated earlier. If the slopes are different, then the points do not lie on the same straight line, and we can immediately conclude that it's not a straight line.
- If we iterate through all the points and the slope remains the same, then all points lie on the same straight line, meaning it is a straight line.
Code Implementation
def check_if_straight_line(points):
if len(points) <= 2:
return True
x_one, y_one = points[0]
x_two, y_two = points[1]
# Calculate the initial slope, avoid division by zero.
if x_two - x_one == 0:
initial_slope = float('inf')
else:
initial_slope = (y_two - y_one) / (x_two - x_one)
for i in range(2, len(points)):
x_current, y_current = points[i]
# Calculate slope between the first point and the current point.
if x_current - x_one == 0:
# Need to handle the vertical line edge case.
current_slope = float('inf')
else:
current_slope = (y_current - y_one) / (x_current - x_one)
# Compare the current slope with the initial slope.
if current_slope != initial_slope:
# Slopes differ, not a straight line.
return False
# All slopes are the same, it's a straight line.
return TrueBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty input coordinates array | Return True, as an empty set of points can be considered on a straight line by default. |
| Input array contains only one point | Return True, because a single point trivially lies on a straight line. |
| All points are the same | Return True, as identical points can be considered to form a degenerate straight line. |
| Vertical line (infinite slope) | Handle the division by zero when calculating the slope by checking for a zero difference in x-coordinates. |
| Horizontal line (zero slope) | The standard slope calculation will correctly handle this case without special modification. |
| Integer overflow when calculating slope differences | Use a data type with a wider range (e.g., long) to store the slope differences or calculate the cross product to avoid division. |
| Floating point precision errors when comparing slopes | Compare slopes with a tolerance (epsilon) to account for potential floating-point inaccuracies. |
| Large number of points to potentially create very steep lines | The algorithm calculates slopes dynamically, so the number of points doesn't impact performance significantly, but the use of long for cross product calculation is advised. |