Check if There is a Valid Path in a Grid #7 Most Asked
MediumYou are given an m x n grid. Each cell of grid represents a street. The street of grid[i][j] can be:
1which means a street connecting the left cell and the right cell.2which means a street connecting the upper cell and the lower cell.3which means a street connecting the left cell and the lower cell.4which means a street connecting the right cell and the lower cell.5which means a street connecting the left cell and the upper cell.6which means a street connecting the right cell and the upper cell.
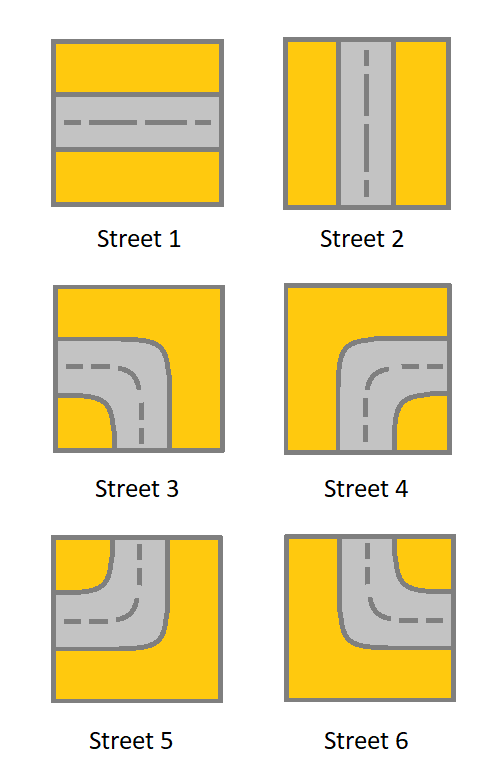
You will initially start at the street of the upper-left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1). The path should only follow the streets.
Notice that you are not allowed to change any street.
Return true if there is a valid path in the grid or false otherwise.
Example 1:
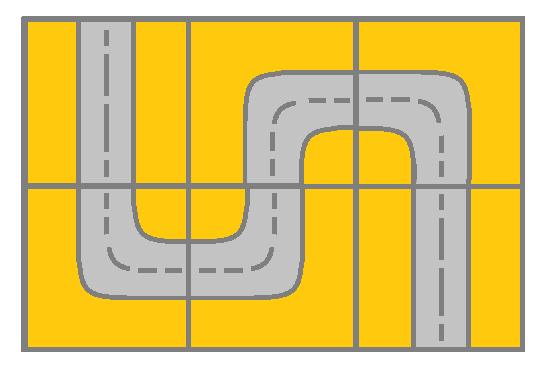
Input: grid = [[2,4,3],[6,5,2]] Output: true Explanation: As shown you can start at cell (0, 0) and visit all the cells of the grid to reach (m - 1, n - 1).
Example 2:

Input: grid = [[1,2,1],[1,2,1]] Output: false Explanation: As shown you the street at cell (0, 0) is not connected with any street of any other cell and you will get stuck at cell (0, 0)
Example 3:
Input: grid = [[1,1,2]] Output: false Explanation: You will get stuck at cell (0, 1) and you cannot reach cell (0, 2).
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 3001 <= grid[i][j] <= 6
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the grid (m and n), and what are the constraints on their values? Can the grid be empty?
- What are the possible integer values for the grid cells, and what are the specific street types they represent (could you provide a mapping)?
- Is it possible for the starting cell (0, 0) or the ending cell (m-1, n-1) to contain a street type that makes it impossible to start or end the path?
- If a valid path exists, is any valid path sufficient, or are there specific criteria for the path (e.g., shortest path, path avoiding certain types of streets)?
- What should I return if there is no valid path found, specifically, should I return null, throw an exception, or is returning false acceptable?
Brute Force Solution
Approach
Imagine you are navigating a maze with pathways. The brute force approach involves trying every possible route through the maze, one step at a time, until you find a path that leads to the exit or you've tried absolutely everything. It's like exploring every single nook and cranny.
Here's how the algorithm would work step-by-step:
- Start at the beginning of the grid, your starting point.
- From your current position, try moving in every possible direction allowed by the current cell's shape.
- If a move takes you outside the grid's boundaries, or to a cell you've already visited in this attempt, abandon that path and try a different direction.
- If a move leads you to the end of the grid, you've found a valid path! Success!
- If none of the possible moves from your current position lead to the end or to a useful new spot, backtrack to the previous cell and try a different direction from there.
- Keep repeating this process: exploring new directions, backtracking when necessary, and checking for success. You are trying every single possible combination of movements through the grid.
- If you've explored every single possible path from the starting point and haven't found a valid path to the end, then there is no valid path.
Code Implementation
def has_valid_path_brute_force(grid):
rows = len(grid)
cols = len(grid[0])
def is_valid_move(row, col):
return 0 <= row < rows and 0 <= col < cols
def get_possible_moves(row, col, street_type):
if street_type == 1:
return [(row, col + 1), (row, col - 1)]
elif street_type == 2:
return [(row + 1, col), (row - 1, col)]
elif street_type == 3:
return [(row, col - 1), (row + 1, col)]
elif street_type == 4:
return [(row, col + 1), (row + 1, col)]
elif street_type == 5:
return [(row, col - 1), (row - 1, col)]
else:
return [(row, col + 1), (row - 1, col)]
def backtrack(row, col, visited):
if row == rows - 1 and col == cols - 1:
return True
street_type = grid[row][col]
possible_moves = get_possible_moves(row, col, street_type)
for next_row, next_col in possible_moves:
if is_valid_move(next_row, next_col) and (next_row, next_col) not in visited:
# Mark the next cell as visited before exploring it.
visited.add((next_row, next_col))
if backtrack(next_row, next_col, visited):
return True
# Backtrack: remove the cell from visited.
visited.remove((next_row, next_col))
return False
# Start the search from the top-left cell.
start_row = 0
start_col = 0
visited = set([(start_row, start_col)])
# Invoke the recursive helper function.
return backtrack(start_row, start_col, visited)
Big(O) Analysis
Optimal Solution
Approach
The core idea is to traverse the grid following the paths defined by each cell's shape, ensuring you stay on a valid route from start to finish. We use a technique to remember where we've already been to avoid getting stuck in loops. By carefully following the paths and remembering our steps, we can determine if a valid route exists.
Here's how the algorithm would work step-by-step:
- Start at the top-left corner of the grid.
- Examine the shape of the current cell to determine which directions you can move (left, right, up, or down).
- Choose a valid direction to move in, based on both the cell's shape and the boundaries of the grid.
- Before moving, mark the current cell as visited to prevent revisiting it later.
- Move to the next cell and repeat the process of checking the shape and choosing a direction.
- If you reach the bottom-right corner, you have found a valid path and can stop.
- If you reach a dead end (no valid moves) or a previously visited cell, backtrack to the previous cell and try a different direction.
- If you have explored all possible paths from the starting point and haven't reached the end, there is no valid path.
Code Implementation
def has_valid_path(grid):
rows = len(grid)
columns = len(grid[0])
visited = set()
def find_path(row, column):
if row == rows - 1 and column == columns - 1:
return True
visited.add((row, column))
current_cell = grid[row][column]
possible_moves = []
if current_cell == 1:
possible_moves = [(0, 1), (0, -1)]
elif current_cell == 2:
possible_moves = [(1, 0), (-1, 0)]
elif current_cell == 3:
possible_moves = [(0, -1), (1, 0)]
elif current_cell == 4:
possible_moves = [(0, 1), (1, 0)]
elif current_cell == 5:
possible_moves = [(0, -1), (-1, 0)]
elif current_cell == 6:
possible_moves = [(0, 1), (-1, 0)]
for move_row, move_column in possible_moves:
new_row = row + move_row
new_column = column + move_column
# Boundary and connectivity check
if 0 <= new_row < rows and 0 <= new_column < columns and \
(new_row, new_column) not in visited:
next_cell = grid[new_row][new_column]
valid_connection = False
if current_cell == 1:
if move_column == 1 and (next_cell in [1, 3, 5]):
valid_connection = True
elif move_column == -1 and (next_cell in [1, 4, 6]):
valid_connection = True
elif current_cell == 2:
if move_row == 1 and (next_cell in [2, 5, 6]):
valid_connection = True
elif move_row == -1 and (next_cell in [2, 3, 4]):
valid_connection = True
elif current_cell == 3:
if move_row == 1 and (next_cell in [2, 5, 6]):
valid_connection = True
elif move_column == -1 and (next_cell in [1, 4, 6]):
valid_connection = True
elif current_cell == 4:
if move_row == 1 and (next_cell in [2, 5, 6]):
valid_connection = True
elif move_column == 1 and (next_cell in [1, 3, 5]):
valid_connection = True
elif current_cell == 5:
if move_row == -1 and (next_cell in [2, 3, 4]):
valid_connection = True
elif move_column == -1 and (next_cell in [1, 4, 6]):
valid_connection = True
elif current_cell == 6:
if move_row == -1 and (next_cell in [2, 3, 4]):
valid_connection = True
elif move_column == 1 and (next_cell in [1, 3, 5]):
valid_connection = True
# Only proceed if the move is valid
if valid_connection:
if find_path(new_row, new_column):
return True
# Backtrack if no path is found
visited.remove((row, column))
return False
# Start path finding from the top-left cell
if find_path(0, 0):
return True
# No valid path exists from start to end
return FalseBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty grid | Return false immediately as there is no path to traverse. |
| Grid with only one cell (1x1) | Return true if the grid is 1x1, because the start and end are the same, representing a valid path. |
| No valid path exists from (0, 0) to (m-1, n-1) | The algorithm should explore all possible paths and return false if the destination is never reached after exploring all accessible cells. |
| Grid dimensions are very large (m and n are close to the maximum allowed integer) | Consider using iterative DFS or BFS to avoid potential stack overflow errors with recursive DFS and to handle large grid sizes efficiently. |
| All street types in the grid are the same, but do not allow a path from start to end. | The path finding algorithm must still correctly identify the lack of a valid path even if all cells have the same type. |
| Street types outside the range [1, 6] | Treat street types outside the valid range as an obstacle or an invalid state, preventing movement through that cell. |
| Grid is a single row or a single column, and the path requires moving in the other dimension. | The path finding algorithm must respect the grid boundaries and street types and correctly detect cases with impossible paths along a single row or column. |
| The path creates a cycle. | Use a visited set to keep track of visited cells, preventing the algorithm from getting stuck in an infinite loop due to cycles. |