Cherry Pickup #4 Most Asked
HardYou are given an n x n grid representing a field of cherries, each cell is one of three possible integers.
0means the cell is empty, so you can pass through,1means the cell contains a cherry that you can pick up and pass through, or-1means the cell contains a thorn that blocks your way.
Return the maximum number of cherries you can collect by following the rules below:
- Starting at the position
(0, 0)and reaching(n - 1, n - 1)by moving right or down through valid path cells (cells with value0or1). - After reaching
(n - 1, n - 1), returning to(0, 0)by moving left or up through valid path cells. - When passing through a path cell containing a cherry, you pick it up, and the cell becomes an empty cell
0. - If there is no valid path between
(0, 0)and(n - 1, n - 1), then no cherries can be collected.
Example 1:
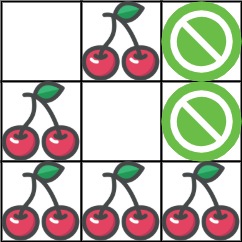
Input: grid = [[0,1,-1],[1,0,-1],[1,1,1]] Output: 5 Explanation: The player started at (0, 0) and went down, down, right right to reach (2, 2). 4 cherries were picked up during this single trip, and the matrix becomes [[0,1,-1],[0,0,-1],[0,0,0]]. Then, the player went left, up, up, left to return home, picking up one more cherry. The total number of cherries picked up is 5, and this is the maximum possible.
Example 2:
Input: grid = [[1,1,-1],[1,-1,1],[-1,1,1]] Output: 0
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 50grid[i][j]is-1,0, or1.grid[0][0] != -1grid[n - 1][n - 1] != -1
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the grid, and what is the maximum possible size of the grid (i.e., maximum rows and columns)?
- Can the cherry values in the grid be negative, zero, or only positive?
- If a cell contains 0 (no cherry), can the robots still move through it?
- What should I return if there is no possible path to collect any cherries?
- Are the starting positions of the robots fixed at (0, 0) and (0, 0) or can they start from different cells in the top-left corner?
Brute Force Solution
Approach
Imagine two people are walking on a grid, collecting cherries. The brute force method involves trying every possible path each person can take and figuring out which combination of paths yields the most cherries.
Here's how the algorithm would work step-by-step:
- Consider all possible paths for the first person to reach the destination (the bottom right corner).
- For each path the first person takes, consider all possible paths for the second person to reach the destination.
- For each pair of paths, figure out how many cherries were picked up. If both people are on the same square, they only pick up those cherries once.
- Keep track of the maximum number of cherries picked up across all possible pairs of paths.
- Once you've exhausted every possible combination of paths for both people, the maximum number of cherries you kept track of is the answer.
Code Implementation
def cherry_pickup_brute_force(grid):
grid_size = len(grid)
max_cherries = 0
def find_all_paths(current_row, current_col):
if current_row == grid_size - 1 and current_col == grid_size - 1:
return [[(current_row, current_col)]]
if current_row >= grid_size or current_col >= grid_size:
return []
paths = []
# Explore moving down
for path in find_all_paths(current_row + 1, current_col):
paths.append([(current_row, current_col)] + path)
# Explore moving right
for path in find_all_paths(current_row, current_col + 1):
paths.append([(current_row, current_col)] + path)
return paths
first_person_paths = find_all_paths(0, 0)
second_person_paths = find_all_paths(0, 0)
# Iterate through all combinations of paths
for first_person_path in first_person_paths:
for second_person_path in second_person_paths:
cherries_collected = 0
visited = set()
# Calculate cherries picked by the first person
for row, col in first_person_path:
if (row, col) not in visited:
cherries_collected += grid[row][col]
visited.add((row, col))
# Calculate cherries picked by the second person
for row, col in second_person_path:
if (row, col) not in visited:
cherries_collected += grid[row][col]
visited.add((row, col))
#Update maximum cherries picked
max_cherries = max(max_cherries, cherries_collected)
return max_cherriesBig(O) Analysis
Optimal Solution
Approach
Imagine two people walking from the top-left to the bottom-right of a grid, collecting cherries along the way. The trick is to think of these two paths as happening simultaneously to avoid re-calculating overlaps and make the problem easier to solve.
Here's how the algorithm would work step-by-step:
- Instead of thinking about two separate trips, imagine the two people walking together at the same time.
- Realize that after the same number of steps, both people will be the same total distance away from the starting point, even if they took different paths.
- Keep track of the maximum number of cherries you can collect at each step for both people, considering all possible paths they could have taken to get there.
- If both people are at the same spot, only count the cherry at that location once.
- Continue this process, moving step by step through the grid, always keeping track of the best cherry count so far for each possible position of the two people.
- The final answer is the maximum number of cherries both people can have when they both reach the bottom-right corner.
Code Implementation
def cherry_pickup(grid):
grid_size = len(grid)
# Initialize DP table to store max cherries.
dp_table = {}
def get_max_cherries(row_1, column_1, row_2):
column_2 = row_1 + column_1 - row_2
# Base case: Out of bounds.
if (row_1 >= grid_size or column_1 >= grid_size or
row_2 >= grid_size or column_2 >= grid_size or
grid[row_1][column_1] == -1 or grid[row_2][column_2] == -1):
return float('-inf')
# Base case: Reached the destination.
if row_1 == grid_size - 1 and column_1 == grid_size - 1:
return grid[row_1][column_1]
# Memoization.
if (row_1, column_1, row_2) in dp_table:
return dp_table[(row_1, column_1, row_2)]
# Calculate cherries collected.
cherries = grid[row_1][column_1]
if row_1 != row_2 or column_1 != column_2:
cherries += grid[row_2][column_2]
# Recursively explore possible paths.
path_1 = get_max_cherries(row_1 + 1, column_1, row_2 + 1)
path_2 = get_max_cherries(row_1 + 1, column_1, row_2)
path_3 = get_max_cherries(row_1, column_1 + 1, row_2 + 1)
path_4 = get_max_cherries(row_1, column_1 + 1, row_2)
max_cherries = cherries + max(path_1, path_2, path_3, path_4)
dp_table[(row_1, column_1, row_2)] = max_cherries
# Store intermediate results for memoization.
return max_cherries
# Start both people at the top-left.
result = get_max_cherries(0, 0, 0)
# Handle negative results.
return max(0, result)Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty grid | Return 0 immediately, as there are no cherries to collect. |
| 1x1 grid | Return the value of the single cell if positive, otherwise 0. |
| Grid with all cells containing 0 | Return 0, as no cherries can be collected. |
| Grid with negative values (e.g., thorns) | Handle negative values as impassable (e.g., -1) and update the DP table accordingly by setting the cherry count to a very low number. |
| Grid with only one path to the destination | The DP algorithm will still correctly compute the optimal solution along the single path. |
| Maximum sized grid (50x50) with max cherry values, potential for integer overflow | Use a data type large enough to store potentially large values in the DP table, such as long. |
| No path to the destination exists | Return 0, as no cherries can be collected if the destination is unreachable. |
| Large grid filled with mostly zero values | The algorithm might take long time traversing zeros, but optimization using memoization (DP) should avoid recomputing. |