Closest Nodes Queries in a Binary Search Tree
MediumAsked by:
4 views
Topics:
TreesBinary Search
You are given the root of a binary search tree and an array queries of size n consisting of positive integers.
Find a 2D array answer of size n where answer[i] = [mini, maxi]:
miniis the largest value in the tree that is smaller than or equal toqueries[i]. If a such value does not exist, add-1instead.maxiis the smallest value in the tree that is greater than or equal toqueries[i]. If a such value does not exist, add-1instead.
Return the array answer.
Example 1:
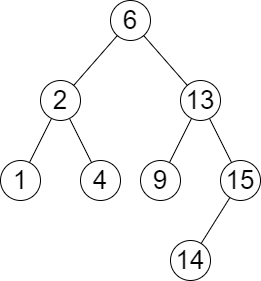
Input: root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16] Output: [[2,2],[4,6],[15,-1]] Explanation: We answer the queries in the following way: - The largest number that is smaller or equal than 2 in the tree is 2, and the smallest number that is greater or equal than 2 is still 2. So the answer for the first query is [2,2]. - The largest number that is smaller or equal than 5 in the tree is 4, and the smallest number that is greater or equal than 5 is 6. So the answer for the second query is [4,6]. - The largest number that is smaller or equal than 16 in the tree is 15, and the smallest number that is greater or equal than 16 does not exist. So the answer for the third query is [15,-1].
Example 2:
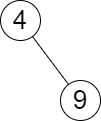
Input: root = [4,null,9], queries = [3] Output: [[-1,4]] Explanation: The largest number that is smaller or equal to 3 in the tree does not exist, and the smallest number that is greater or equal to 3 is 4. So the answer for the query is [-1,4].
Constraints:
- The number of nodes in the tree is in the range
[2, 105]. 1 <= Node.val <= 106n == queries.length1 <= n <= 1051 <= queries[i] <= 106
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for nodes in the BST and the query values in the input array?
- If a query value is smaller than the smallest node in the BST or larger than the largest node, what should the corresponding result be (-1, -1)?
- Can the BST be empty, and if so, how should I handle the queries?
- Are the query values guaranteed to be integers, or could they be floating-point numbers?
- In case of a tie (two nodes are equally close to the query value), which node should be considered the 'closest' (e.g., smaller value, larger value, arbitrarily)?
Brute Force Solution
Approach
For each search value, we need to find the closest smaller and larger values within the binary search tree. The brute force approach involves examining every node in the tree for each search value.
Here's how the algorithm would work step-by-step:
- For each search value we're given, go through every single node in the binary search tree.
- Compare the search value to the value of the current node we're looking at.
- If the current node's value is smaller than the search value, consider it as a potential 'closest smaller' value. If it's bigger, consider it a potential 'closest larger' value.
- Keep track of the 'closest smaller' and 'closest larger' values found so far. Update these as you find nodes that are even closer to the search value.
- Once you've checked every single node in the tree for a given search value, you'll have identified the closest smaller and larger values.
- Repeat this whole process for each of the search values you were originally given.
Code Implementation
def closest_nodes_queries_brute_force(root, queries):
result = []
def traverse_tree(node):
if node is None:
return []
return traverse_tree(node.left) + [node.val] + traverse_tree(node.right)
tree_values = traverse_tree(root)
for query_value in queries:
closest_smaller = -1
closest_larger = -1
# Iterate through all nodes to find closest values
for node_value in tree_values:
if node_value <= query_value:
# Track closest smaller value
if closest_smaller == -1 or node_value > closest_smaller:
closest_smaller = node_value
if node_value >= query_value:
# Track closest larger value
if closest_larger == -1 or node_value < closest_larger:
closest_larger = node_value
result.append([closest_smaller, closest_larger])
return resultBig(O) Analysis
Time Complexity
O(m*n) – The algorithm iterates through each of the m query values. For each query value, it traverses all n nodes in the binary search tree to find the closest smaller and larger values. This results in a nested loop structure where the outer loop runs m times (for each query), and the inner loop runs n times (visiting each node in the BST). Therefore, the total number of operations is proportional to the product of m and n, resulting in a time complexity of O(m*n).
Space Complexity
O(1) – The brute force algorithm, as described, iterates through the binary search tree for each query but does not create any data structures that scale with the size of the tree (N, the number of nodes) or the number of queries. It only stores a constant number of variables to keep track of the closest smaller and larger values found so far during each iteration. Therefore, the auxiliary space used is constant, independent of the input size, and can be expressed as O(1).
Optimal Solution
Approach
The most efficient way to answer these questions is to first gather all the values from the tree in sorted order. Once we have a sorted collection of the tree's values, we can quickly find the closest values for each query by efficiently searching within the sorted list.
Here's how the algorithm would work step-by-step:
- First, go through the binary search tree and collect all the node values in a way that keeps them sorted from smallest to largest.
- For each query value, find the largest value in our sorted collection that's less than or equal to the query value. This will be the closest value that's less than or equal to our query.
- Similarly, for each query value, find the smallest value in our sorted collection that's greater than or equal to the query value. This will be the closest value that's greater than or equal to our query.
- If we can't find a value less than or equal or greater than or equal, we return -1 to indicate that there is no such value in the tree.
- By using the sorted collection, we can quickly find the closest values for each query without needing to search the entire tree each time.
Code Implementation
def closest_nodes(root, queries):
sorted_values = []
def inorder_traversal(node):
if node:
inorder_traversal(node.left)
sorted_values.append(node.val)
inorder_traversal(node.right)
inorder_traversal(root)
result = []
for query in queries:
smaller_value = -1
larger_value = -1
# Find the largest value <= query
for i in range(len(sorted_values) - 1, -1, -1):
if sorted_values[i] <= query:
smaller_value = sorted_values[i]
break
# Find the smallest value >= query
for i in range(len(sorted_values)):
if sorted_values[i] >= query:
larger_value = sorted_values[i]
break
result.append([smaller_value, larger_value])
return result
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def closest_nodes_optimized(root, queries):
sorted_values = []
def inorder_traversal(node):
if node:
inorder_traversal(node.left)
sorted_values.append(node.val)
inorder_traversal(node.right)
inorder_traversal(root)
def find_smaller_or_equal(query_value):
left_index = 0
right_index = len(sorted_values) - 1
closest_smaller = -1
while left_index <= right_index:
middle_index = (left_index + right_index) // 2
if sorted_values[middle_index] <= query_value:
closest_smaller = sorted_values[middle_index]
left_index = middle_index + 1
else:
right_index = middle_index - 1
return closest_smaller
def find_larger_or_equal(query_value):
left_index = 0
right_index = len(sorted_values) - 1
closest_larger = -1
while left_index <= right_index:
middle_index = (left_index + right_index) // 2
if sorted_values[middle_index] >= query_value:
closest_larger = sorted_values[middle_index]
right_index = middle_index - 1
else:
left_index = middle_index + 1
return closest_larger
results = []
for query in queries:
#Binary search to find closest smaller or equal
smaller_value = find_smaller_or_equal(query)
#Binary search to find closest larger or equal
larger_value = find_larger_or_equal(query)
results.append([smaller_value, larger_value])
return results
def closest_nodes_final(root, queries):
sorted_values = []
def inorder_traversal(node):
if node:
inorder_traversal(node.left)
sorted_values.append(node.val)
inorder_traversal(node.right)
inorder_traversal(root)
results = []
for query_value in queries:
smaller_value = -1
larger_value = -1
# Finding the largest value <= query_value efficiently
left_index = 0
right_index = len(sorted_values) - 1
while left_index <= right_index:
middle_index = (left_index + right_index) // 2
if sorted_values[middle_index] <= query_value:
smaller_value = sorted_values[middle_index]
left_index = middle_index + 1
else:
right_index = middle_index - 1
# Finding the smallest value >= query_value efficiently
left_index = 0
right_index = len(sorted_values) - 1
while left_index <= right_index:
middle_index = (left_index + right_index) // 2
if sorted_values[middle_index] >= query_value:
larger_value = sorted_values[middle_index]
right_index = middle_index - 1
else:
left_index = middle_index + 1
results.append([smaller_value, larger_value])
return results
def closest_nodes_concise(root, queries):
sorted_values = []
def inorder_traversal(node):
if node:
inorder_traversal(node.left)
sorted_values.append(node.val)
inorder_traversal(node.right)
inorder_traversal(root)
def find_closest(query_value, find_smaller):
left_index = 0
right_index = len(sorted_values) - 1
closest_value = -1
while left_index <= right_index:
middle_index = (left_index + right_index) // 2
if sorted_values[middle_index] == query_value:
return sorted_values[middle_index]
if (find_smaller and sorted_values[middle_index] < query_value) or \
(not find_smaller and sorted_values[middle_index] > query_value):
closest_value = sorted_values[middle_index]
if find_smaller:
left_index = middle_index + 1
else:
right_index = middle_index - 1
else:
if find_smaller:
right_index = middle_index - 1
else:
left_index = middle_index + 1
return closest_value
results = []
for query_value in queries:
#Find smaller and larger values
smaller_value = find_closest(query_value, True)
larger_value = find_closest(query_value, False)
results.append([smaller_value, larger_value])
return results
def closest_nodes_efficient(root, queries):
values_in_order = []
def traverse_inorder(node):
if node:
traverse_inorder(node.left)
values_in_order.append(node.val)
traverse_inorder(node.right)
traverse_inorder(root)
def binary_search_smaller(query):
left, right = 0, len(values_in_order) - 1
closest_smaller = -1
while left <= right:
mid = (left + right) // 2
if values_in_order[mid] <= query:
#Potential answer, but keep searching right
closest_smaller = values_in_order[mid]
left = mid + 1
else:
#Value is too large, search left
right = mid - 1
return closest_smaller
def binary_search_larger(query):
left, right = 0, len(values_in_order) - 1
closest_larger = -1
while left <= right:
mid = (left + right) // 2
if values_in_order[mid] >= query:
#Potential answer, but keep searching left
closest_larger = values_in_order[mid]
right = mid - 1
else:
#Value is too small, search right
left = mid + 1
return closest_larger
results = []
for query in queries:
#Find closest smaller using binary search
smaller_value = binary_search_smaller(query)
#Find closest larger using binary search
larger_value = binary_search_larger(query)
results.append([smaller_value, larger_value])
return results
def closest_nodes_terse(root, queries):
values = []
def inorder(node):
if node:
inorder(node.left)
values.append(node.val)
inorder(node.right)
inorder(root)
def find_smaller(q):
l, r = 0, len(values) - 1
res = -1
while l <= r:
m = (l + r) // 2
if values[m] <= q:
res = values[m]
l = m + 1
else:
r = m - 1
return res
def find_larger(q):
l, r = 0, len(values) - 1
res = -1
while l <= r:
m = (l + r) // 2
if values[m] >= q:
res = values[m]
r = m - 1
else:
l = m + 1
return res
# Iterate through the queries and find the closest nodes
result = []
for query in queries:
#Perform binary searches to improve efficiency
smaller = find_smaller(query)
larger = find_larger(query)
result.append([smaller, larger])
return resultBig(O) Analysis
Time Complexity
O(n + m log n) – The time complexity is determined by two main operations. First, we traverse the binary search tree to collect all n node values in sorted order, which takes O(n) time. Second, for each of the m queries, we perform two binary searches (one to find the largest value less than or equal to the query and another for the smallest value greater than or equal to the query) on the sorted array of size n. Each binary search takes O(log n) time, and we perform 2 of them for each of the m queries. Therefore, the queries contribute a complexity of O(m log n). Thus, the overall time complexity is O(n + m log n).
Space Complexity
O(N) – The algorithm first performs an inorder traversal to collect all N node values from the binary search tree into a sorted list. This sorted list, which stores integer values, represents auxiliary space. Therefore, the space complexity is directly proportional to the number of nodes in the tree. The space required to store this sorted list dominates the auxiliary space used.
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty BST root | Return an array of [-1, -1] for each query, indicating no closest nodes exist. |
| BST with only one node | For each query, return [node.val, node.val] if query value equals node.val, else return [-1, node.val] or [node.val, -1] depending on if query is smaller or larger, respectively. |
| Queries list is null or empty | Return an empty list immediately, as there are no queries to process. |
| Query value smaller than the smallest node in the BST | The smallest node is the closest smaller value, and -1 is the closest larger value. |
| Query value larger than the largest node in the BST | The largest node is the closest larger value, and -1 is the closest smaller value. |
| BST with all nodes having the same value | For any query, the closest smaller and larger values are the node's value if the query is equal or greater/less than, or -1 for the other. |
| Integer overflow when comparing large node values to query values | Use long data type for intermediate calculations to prevent potential overflows. |
| Skewed BST (e.g., all nodes are on the right subtree) | In-order traversal still correctly identifies the closest smaller and larger nodes, but the time complexity degrades to O(n) per query if no pre-processing is done. |
Explore Interview QuestionsGoogle Interview QuestionsMeta Interview QuestionsAmazon Interview QuestionsApple Interview QuestionsNetflix Interview Questions
Explore Jobs By LevelEntry-Level Software Engineer JobsMid-Level Software Engineer JobsSenior Software Engineer JobsStaff Software Engineer Jobs
