Construct Binary Search Tree from Preorder Traversal
MediumGiven an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.
It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.
A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.
A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.
Example 1:
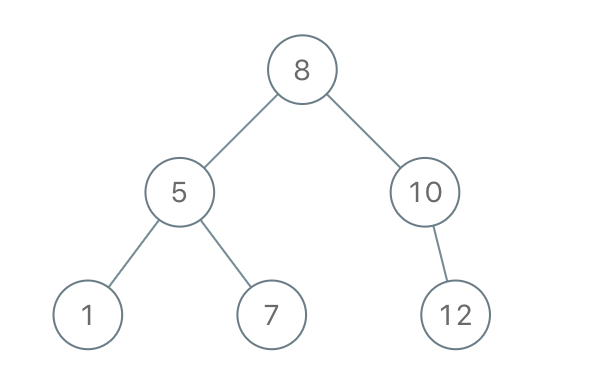
Input: preorder = [8,5,1,7,10,12] Output: [8,5,10,1,7,null,12]
Example 2:
Input: preorder = [1,3] Output: [1,null,3]
Constraints:
1 <= preorder.length <= 1001 <= preorder[i] <= 1000- All the values of
preorderare unique.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the expected range of values in the preorder traversal array? Should I expect only positive integers, or can there be negative numbers or zeros?
- Can the input preorder traversal array be empty or null? If so, what should I return?
- Are the values in the preorder traversal guaranteed to represent a valid binary search tree? Or could there be an invalid sequence that doesn't form a BST?
- If duplicate values are present in the input array, how should they be handled in the BST construction? Should they all go to the left subtree, right subtree, or is there a specific ordering requirement?
- Does the problem require a perfectly balanced BST? Or is any valid BST constructed from the preorder traversal acceptable?
Brute Force Solution
Approach
The brute force approach for building a binary search tree from a preorder traversal considers all possible tree structures. It explores every way to place each number from the preorder list as a node in the tree, and then checks if the resulting tree is a valid binary search tree and if its preorder traversal matches the input.
Here's how the algorithm would work step-by-step:
- Take the first number from the list. This will be the root of our tree.
- For the next number in the list, try placing it as the left child of the root.
- Now, with the next number, try placing it as either the left or right child of the root, or as a child of the first left child we made. Explore all these options.
- Continue this process for each remaining number: for each, try placing it in every available spot in the tree that we've built so far.
- After placing all the numbers, check if the tree we built is a valid binary search tree (smaller values on the left, larger values on the right).
- Also, check if the preorder traversal of the tree matches the original list of numbers.
- If the tree is valid and the preorder traversal matches, save this tree as a possible solution.
- Repeat the entire process from step 2, exploring all possible arrangements of numbers into tree structures.
- Finally, from all the valid tree structures we found, pick any one. Since the problem statement guarantees a solution, at least one valid tree will be found.
Code Implementation
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def construct_binary_search_tree_from_preorder(preorder):
def is_valid_binary_search_tree(root, min_value=float('-inf'), max_value=float('inf')):
if not root:
return True
if root.value <= min_value or root.value >= max_value:
return False
return is_valid_binary_search_tree(root.left, min_value, root.value) and \
is_valid_binary_search_tree(root.right, root.value, max_value)
def get_preorder_traversal(root, traversal=[]):
if root:
traversal.append(root.value)
get_preorder_traversal(root.left, traversal)
get_preorder_traversal(root.right, traversal)
return traversal
def build_tree(nodes):
if not nodes:
return None
root_node = TreeNode(nodes[0])
remaining_nodes = nodes[1:]
trees = [root_node]
for node_value in remaining_nodes:
new_trees = []
for current_tree in trees:
possible_trees = generate_possible_insertions(current_tree, node_value)
new_trees.extend(possible_trees)
trees = new_trees
return trees
def generate_possible_insertions(root, node_value):
possible_trees = []
def insert_node(root, node_value):
if not root:
return TreeNode(node_value)
new_root = TreeNode(root.value)
new_root.left = root.left
new_root.right = root.right
if node_value < new_root.value:
new_root.left = insert_node(new_root.left, node_value)
else:
new_root.right = insert_node(new_root.right, node_value)
return new_root
# Create a copy of the tree to prevent modification
queue = [root]
while queue:
current_node = queue.pop(0)
#Create tree with node_value inserted into tree
new_root = TreeNode(root.value)
new_root.left = root.left
new_root.right = root.right
inserted_tree = insert_node(new_root, node_value)
possible_trees.append(inserted_tree)
if current_node.left:
queue.append(current_node.left)
if current_node.right:
queue.append(current_node.right)
#insert node_value as the root
new_node = TreeNode(node_value)
new_node.left = root
possible_trees.append(new_node)
return possible_trees
all_possible_trees = build_tree(preorder)
for tree in all_possible_trees:
# Check if the tree is a valid BST
if is_valid_binary_search_tree(tree):
# Verify the preorder traversal matches the input
if get_preorder_traversal(tree) == preorder:
#Ensure valid tree is returned
return tree
return NoneBig(O) Analysis
Optimal Solution
Approach
The task is to create a special tree (a binary search tree) using a specific ordering (preorder). Instead of building the tree branch by branch in a simple way, we use the properties of the preorder to know what the valid ranges for the tree can be. This avoids creating invalid trees.
Here's how the algorithm would work step-by-step:
- Start with the first value from the given order; this will be the root of the entire tree.
- For each subsequent value, we know it must be placed as either a left or right child of some node in the tree.
- The key is to keep track of the allowed range of values for the right subtree of each node as we go along. In essence, for any node, we track a lower bound representing the minimum value any node in its right subtree can have.
- If the current value is smaller than the current node, we add the new value as the left child, because a left child of a node must be smaller than that node.
- If the current value is larger than the current node, we add the new value as the right child, but only if it is also smaller than the upper limit of the valid range for a right subtree. This means that we move up the tree until we find a parent where the new node is still valid (greater than the parent and less than the upper range value), and then make it the right child of that parent.
- We repeat this process, adding values to the tree based on the order given, while respecting the ranges of values valid for the left and right subtrees. These values for the upper ranges are determined when we create a left child.
- By correctly placing nodes based on these ranges, we ensure the tree is a valid binary search tree, without needing to try all possible placements.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def construct_binary_search_tree_from_preorder(preorder):
index = 0
def helper(lower_bound=float('-inf'), upper_bound=float('inf')):
nonlocal index
if index == len(preorder):
return None
current_value = preorder[index]
# If outside bounds, this value doesn't belong here
if current_value < lower_bound or current_value > upper_bound:
return None
index += 1
root = TreeNode(current_value)
# Left child must be smaller than root
root.left = helper(lower_bound, current_value)
# Right child must be larger than root AND
# smaller than upper bound
root.right = helper(current_value, upper_bound)
return root
# Kick off the recursion with no bounds
return helper()Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty preorder array | Return null, indicating an empty tree as there's no input to construct from. |
| Preorder array with a single element | Create a root node with that single element's value and return the root. |
| Preorder array representing a completely right-skewed tree (monotonically increasing) | The algorithm should handle this case correctly by inserting each node as the right child of the previous, although performance degrades to O(n^2) without optimization. |
| Preorder array representing a completely left-skewed tree (monotonically decreasing) | The algorithm should handle this case by inserting each node as the left child of the previous, performance degrades to O(n^2) without optimization. |
| Preorder array with duplicate values | The algorithm should build a BST where duplicate values are placed either in left or right subtree consistently based on the BST construction rules; this needs to be clarified in the problem definition. |
| Integer overflow if the input values are very large | Consider using long data type or throwing an exception if the values exceed the maximum integer value to prevent unexpected behavior. |
| Very large input array (potential stack overflow with recursive solutions) | Implement the solution iteratively to avoid stack overflow errors for extremely large input sizes. |
| Preorder array contains all the same value | A valid binary search tree can be formed, but all nodes will be added to the left (or right consistently) of the root, depending on implementation. |